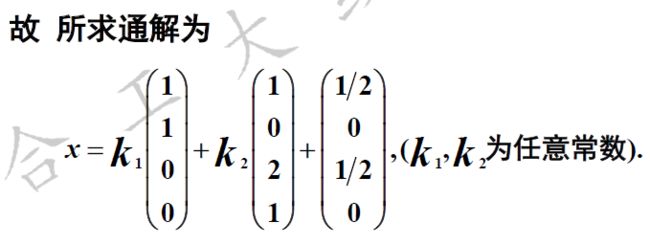MATLAB中矩阵方程求解的实现
一、矩阵方程
1、定义:
2、分类
http://naotu.baidu.com/file/14d36860667d356a54490320cdab2950?token=56a299fe0e0815fe
二、M代码实现
1、M代码
1 function d=CDBH_for_sov_JZFC(a,b) 2 [m1,n1]=size(a); 3 [m2,n2]=size(b); 4 c=[a,b]; 5 ra=rank(a); %矩阵a的秩 6 rb=rank(b); %矩阵b的秩 7 rc=rank(c); %矩阵[a,b]的秩 8 zero=zeros(m2,n2); %构造与b规格相同的零矩阵 9 pj=zero~=b; %确定b中非零元素的个数 10 pj=sum(pj); 11 pj=sum(abs(b)); %更新,把判据改为b中所有值的绝对值之和 12 global i1; %用于阶梯型的计算 13 global i0; %用于阶梯型的计算,其值为当前列于当前行的差值 14 global cx; %用于记录阶梯型的首个元素的位置 15 i1=0; 16 i0=0; 17 x_fqc=[]; %非齐次计算中,用于记录阶梯型的首个元素的位置 18 x_qc=[]; %在齐次计算中,用于记录阶梯型的首个元素的位置 19 cx=[]; 20 if m1~=m2 21 error('输入有误,无法计算'); 22 return; 23 end 24 switch pj 25 %这种情况为其次方程组 26 case 0 27 switch rc 28 %这种情况只有零解 29 case n1 30 31 d=zeros(n1,1); 32 %disp(d); 33 34 %这种情况有基础解系 35 case num2cell([0:n1-1]) 36 %求解思路: 37 %一.矩阵变换 38 %1)化为行阶梯型 39 %2)化为标准型 40 %二.求基础解系 41 %1)分别取非线性向量 42 %2)则线性向量的值为,上述向量对应元素的相反数 43 %三.输出结果 44 45 %一、矩阵变换 46 for i=1:m1-1; %需要对行数-1行进行行变换 47 %选中了第i行 48 %如果都为非线性相关的向量,则阶梯的行列数相等,若存在线性相 49 %的向量,则需要构造一个i0来表示阶梯对应的列,并用i1表示列于 50 %行数的差值。 51 i0=i1+i; 52 %因为i1的值根据本行元素具体情况确定,因此需要注意,应当在这 53 %个for循环内完成下三角、化为1、上三角的所有操作。 54 %Step01 检查阶梯元素是否等于零 55 % 若等于零,则需要与第一个不为零的行对调,若全为零, 56 % 则i1+1,并再次循环。 57 pj_01=0;%初始化以下循环的判据 58 while pj_01==0 %利用判据pj_01来判断是否需要再次循环,在循环中,通过修改pj的值来跳出循环。 59 pj_01=1; %没有特殊情况执行完跳出循环 60 i0=i+i1; 61 if c(i,i0)==0 62 %01 找到第i0列,i行及以下第一个非零元素的位置k 63 k=find(c([i+1:end],i0)); 64 %k=k(1); 65 %02 将k行与i行对调(若k为空集,应当i1+1并再循环) 66 if k~=[]; %k不为空集时,将k行与i行对调 67 k=k(1); 68 e=c(i,:); 69 c(i,:)=c(k,:); 70 c(k,:)=e; 71 pj_01=1; 72 elseif isempty(k)==1; %k为空集时,i1+1并再循环 73 i1=+1; 74 i0=i1+i; 75 pj_01=0; %将判据设为0,再次循环 76 end 77 end 78 end 79 i0=i1+i; 80 x_qc=[x_qc,i0]; %将此时的列位置进行记录 81 %Step2 检查阶梯元素是否为1,若不为1,则将其化为1 82 if c(i,i0)~=0&&c(i,i0)~=0; 83 c(i,:)=c(i,:)/c(i,i0); 84 end 85 %Step3 将i0列,第i行一下的元素消减为0 86 for j=i+1:m1 87 if c(j,i0)~=0 88 c(j,:)=c(j,:)-c(j,i0)*c(i,:); 89 end 90 end 91 %Step4 将i0列,第i行一上的元素消减为0 92 for j=1:i-1 93 if c(j,i0)~=0 94 c(j,:)=c(j,:)-c(j,i0)*c(i,:); 95 end 96 end 97 end 98 %更新!检查最后一行 99 if sum(abs(c(m1,[1:n1])))~=0 100 c(m1,:)=c(m1,:)/c(m1,n1); 101 for j=1:m1-1 102 if c(j,n1)~=0 103 c(j,:)=c(j,:)-c(j,n1)*c(m1,:); 104 end 105 end 106 end 107 108 %成功化为标准型 109 %disp(c) 110 %二、求基础解系 111 %依次选定线性相关向量所在列,查找对应非线性相关的元素的值,并将其取负,放入解系矩阵。 112 %Step1 根据x_qc构造线性相关向量位置向量,构造基础解系矩阵 113 no_x_qc=ones(1,n1); %初始化与a列咧数相等的1向量 114 no_x_qc(x_qc)=0; %其中线性无关向量位置设为0 115 no_x_qc=find(no_x_qc); %找到非零元素位置,命名为no_x_qc 116 jcjx=zeros(n1,rc); %初始化基础解系(行:A的列,列:C的秩) 117 %Step2 选定线性相关所在列(使用for循环) 118 for i=1:length(no_x_qc) 119 120 %Step3 查找该列中,线性无关向量对应的元素的值 121 for j=1:length(x_qc) 122 Psi=c(j,no_x_qc(i)); 123 %Step4 将查找到的值取负,并放入基础解系的第i列的相应位置 124 Psi=Psi*-1; 125 jcjx(x_qc(j),i)=Psi; 126 end 127 %Step5 将基础解系中,当前列对应的位置的元素赋值为1 128 jcjx(no_x_qc(i),i)=1; 129 end 130 %disp(jcjx) 131 %三、输出结果 132 disp '齐次型,结果为基础解系' 133 d=jcjx; 134 disp 'x1' 135 disp '... = k1*psi1+...+kr*psir' 136 disp 'xn' 137 otherwise 138 error('输入有误,无法计算'); 139 return; 140 end 141 %这种话情况为非齐次方程 142 otherwise 143 %这种情况无解 144 if ra<rc 145 error('非齐次方程组无解'); 146 return; 147 %这种情况唯一解 148 elseif ra==rc&&rc==n1 %这时,a必然为方阵,但是可以使用上述齐次方程的解法 149 %思路: 150 %一、矩阵变换 151 %二、求解 152 %三、输出结果 153 154 %一、矩阵变换 155 for i=1:m1-1; %需要对行数-1行进行行变换 156 %选中了第i行 157 %如果都为非线性相关的向量,则阶梯的行列数相等,若存在线性相 158 %的向量,则需要构造一个i0来表示阶梯对应的列,并用i1表示列于 159 %行数的差值。 160 i0=i1+i; 161 %因为i1的值根据本行元素具体情况确定,因此需要注意,应当在这 162 %个for循环内完成下三角、化为1、上三角的所有操作。 163 %Step01 检查阶梯元素是否等于零 164 % 若等于零,则需要与第一个不为零的行对调,若全为零, 165 % 则i1+1,并再次循环。 166 pj_01=0;%初始化以下循环的判据 167 while pj_01==0 %利用判据pj_01来判断是否需要再次循环,在循环中,通过修改pj的值来跳出循环。 168 pj_01=1; %没有特殊情况执行完跳出循环 169 i0=i+i1; 170 if c(i,i0)==0 171 %01 找到第i0列,i行及以下第一个非零元素的位置k 172 k=find(c([i+1:end],i0)); 173 %k=k(1); 174 %02 将k行与i行对调(若k为空集,应当i1+1并再循环) 175 if k~=[]; %k不为空集时,将k行与i行对调 176 k=k(1); 177 e=c(i,:); 178 c(i,:)=c(k,:); 179 c(k,:)=e; 180 pj_01=1; 181 elseif isempty(k)==1; %k为空集时,i1+1并再循环 182 i1=+1; 183 i0=i1+i; 184 pj_01=0; %将判据设为0,再次循环 185 end 186 end 187 end 188 i0=i1+i; 189 x_qc=[x_qc,i0]; %将此时的列位置进行记录 190 %Step2 检查阶梯元素是否为1,若不为1,则将其化为1 191 if c(i,i0)~=0&&c(i,i0)~=0; 192 c(i,:)=c(i,:)/c(i,i0); 193 end 194 %Step3 将i0列,第i行一下的元素消减为0 195 for j=i+1:m1 196 if c(j,i0)~=0 197 c(j,:)=c(j,:)-c(j,i0)*c(i,:); 198 end 199 end 200 %Step4 将i0列,第i行一上的元素消减为0 201 for j=1:i-1 202 if c(j,i0)~=0 203 c(j,:)=c(j,:)-c(j,i0)*c(i,:); 204 end 205 end 206 end 207 %更新!检查最后一行 208 if sum(abs(c(m1,[1:n1])))~=0 209 c(m1,:)=c(m1,:)/c(m1,n1); 210 for j=1:m1-1 211 if c(j,n1)~=0 212 c(j,:)=c(j,:)-c(j,n1)*c(m1,:); 213 end 214 end 215 end 216 217 %成功化为标准型 218 %disp(c) 219 %二、求解 220 %c变换后,其b的位置的数据即为解 221 jx=c(:,[n1+1:end]); 222 %三、输出结果 223 d=jx; 224 disp '非齐次型,唯一解' 225 226 %无穷多解 227 elseif ra==rc&&rc<n1 228 %思路: 229 %一、矩阵变换(利用齐次方程的代码) 230 for i=1:m1-1; %需要对行数-1行进行行变换 231 %选中了第i行 232 %如果都为非线性相关的向量,则阶梯的行列数相等,若存在线性相 233 %的向量,则需要构造一个i0来表示阶梯对应的列,并用i1表示列于 234 %行数的差值。 235 i0=i1+i; 236 %因为i1的值根据本行元素具体情况确定,因此需要注意,应当在这 237 %个for循环内完成下三角、化为1、上三角的所有操作。 238 %Step01 检查阶梯元素是否等于零 239 % 若等于零,则需要与第一个不为零的行对调,若全为零, 240 % 则i1+1,并再次循环。 241 pj_01=0;%初始化以下循环的判据 242 while pj_01==0 %利用判据pj_01来判断是否需要再次循环,在循环中,通过修改pj的值来跳出循环。 243 pj_01=1; %没有特殊情况执行完跳出循环 244 i0=i+i1; 245 if c(i,i0)==0 246 %01 找到第i0列,i行及以下第一个非零元素的位置k 247 k=find(c([i+1:end],i0)); 248 %k=k(1); 249 %02 将k行与i行对调(若k为空集,应当i1+1并再循环) 250 if k~=[]; %k不为空集时,将k行与i行对调 251 k=k(1); 252 e=c(i,:); 253 c(i,:)=c(k,:); 254 c(k,:)=e; 255 pj_01=1; 256 elseif isempty(k)==1; %k为空集时,i1+1并再循环 257 i1=+1; 258 i0=i1+i; 259 pj_01=0; %将判据设为0,再次循环 260 end 261 end 262 end 263 i0=i1+i; 264 x_qc=[x_qc,i0]; %将此时的列位置进行记录 265 %Step2 检查阶梯元素是否为1,若不为1,则将其化为1 266 if c(i,i0)~=0&&c(i,i0)~=0; 267 c(i,:)=c(i,:)/c(i,i0); 268 end 269 %Step3 将i0列,第i行一下的元素消减为0 270 for j=i+1:m1 271 if c(j,i0)~=0 272 c(j,:)=c(j,:)-c(j,i0)*c(i,:); 273 end 274 end 275 %Step4 将i0列,第i行一上的元素消减为0 276 for j=1:i-1 277 if c(j,i0)~=0 278 c(j,:)=c(j,:)-c(j,i0)*c(i,:); 279 end 280 end 281 end 282 %更新!检查最后一行 283 if sum(abs(c(m1,[1:n1])))~=0 284 c(m1,:)=c(m1,:)/c(m1,n1); 285 for j=1:m1-1 286 if c(j,n1)~=0 287 c(j,:)=c(j,:)-c(j,n1)*c(m1,:); 288 end 289 end 290 end 291 292 %成功化为标准型 293 %disp(c) 294 %二、求特解Psit 295 x_fqc=x_qc; %为了便于阅读,使用x_fqc代替x_qc 296 Psit=zeros(1,n1); %初始化特解(长度:a的列数) 297 nx=length(x_fqc); %nx为线性无关向量的数量 298 for i=1:nx 299 ip=x_fqc(i); 300 Psit1=c(:,[n1+1:end]); 301 Psit(ip)=Psit1(i); 302 disp(Psit); 303 end 304 Psit=Psit'; 305 %三、构造对应齐次方程,并解出基础解系 306 b1=zeros(size(b)); 307 308 px=ones(1,n1); 309 px(x_fqc)=0; 310 px=find(px); 311 npx=length(x_fqc); 312 a1=a; 313 %for i=1:npx 314 % ipx=px(i); 315 % a1(:,ipx)=a1(:,ipx)*-1; 316 % disp(a1); 317 %end 318 319 d1=CDBH_for_sov_JZFC(a1,b1); 320 %四、构造通解 321 tj=[d1,Psit]; 322 %五、输出结果 323 d=tj; 324 disp '非齐次,一般解:' 325 disp 'x=k1*psi1+...+kn*psin+psit' 326 else 327 error('输入有误,无法计算'); 328 return; 329 end 330 end
2、例子(用于验证)
(1)齐次方程(无限解):
1 a=[1,1,-1,-1;2,-5,3,2;7,-7,3,1]; 2 b=[0,0,0]';
结果:
(2)非齐次方程(唯一解):
1 a=[89,14,81,19;95,25,24,25;54,84,92,61;13,25,34,47]; 2 b=[436,317,742,353]';
结果:
>>x =
1
2
3
4
(3)非齐次方程(无限解):
1 a=[1,-1,-1,1;1,-1,1,-3;1,-1,-2,3]; 2 b=[0,1,-1/2]';
结果: