1、Q&A
1)Q:今天为什么不讲有理数啊?
A:emm..这个不讲。。只要知道任何一个有理数都可以表示成 p / q (p, q为整数)的形式就可以啦~
2)Q:数轴?我都会了咋办?
A:你可以再看看,这里的数轴——放心好了不是数轴。
Q2::那是什么?
A2:你往下看不就知道了233
2、进入正题——数轴
好, 那么大家认为什么是数轴?
应该是这个样子:
对吧?
数轴上面能表示一些什么数呢?
实数!
这就是我为什么让你再看看——实数这个概念你真的了解吗?
顺便说一下,因为表示所有实数,也就是每一个实数都在数轴上有一个唯一确定的点,所以普通的数轴又被称为实数轴。
3、开心一下——实数
刚才讲到了实数,那么啥是实数呢?
首先它包含有理数。
不同点就在于它还包含了另一类数——无理数!
什么是无理数呢?
乱扯一个小故事:从前有个神仙叫做毕达哥拉斯,认为所有的数都是有理数,然鹅——
在乘船的时候,他的弟子问了这么一个问题:腰长为1的等腰直角三角形的小编长度为多少?
当时已经推导出勾股定理的毕达哥拉斯就在想:什么数的平方等于2呢?
1?1.1?1.2?...
绞尽脑汁想不出来,于是他为了自己的学说,把那个人扔到了水里。。。
后来人们才意识到毕达哥拉斯确实是错的:还存在一种数,它不能表示为两数之比,叫做无理数。
一个数的平方是2,这个数被记做√2,。√这个运算被记做开方运算。
所以发现没有,数域的扩充有时候是要人命的——有个人打猎的时候死了,整数头猎物没办法平均分了,于是就有有理数了。毕达哥拉斯的弟子由于一个问题死了,于是就有无理数和实数了QwQ
4、殊途同归——还是数轴,不是数轴
认识完实数,我们是不是就要开始寻找那个数轴上的对应点了?
注意:下方高能请做好准备
1)请在数轴上表示出√2.
咋做呢?首先-√2和√2其实是一样的,只不过是对称点罢了。
没有数轴的限制,你会不会画呢?
很简单!只要画一个边长为1, 1的直角三角形,那条边就是√2了
如果有数轴呢?
注意,数轴的存在只不过是给了这个线段一个方向(学过平面向量的同学会心一笑),我们只是需要一个工具,转变——或者说旋转一下这个定长线段。
圆!
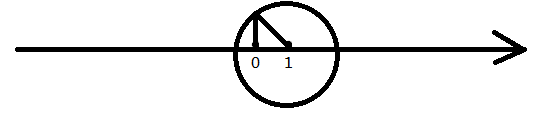
于是我们可以有这样子的图片:
图中斜边就是√2的长度,利用一个半径为√2的圆可以描绘出数轴上的√2.
发散一下思维:你看看这个圆和数轴有几个交点?
2个!所以另一个点的表达式如何描述呢?
首先圆的半径长度是√2, 直径就是2√2,从原点出发到远点右侧的那个点的距离是1+√2,也就是说圆与线段左侧的交点代表了1-√2!