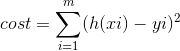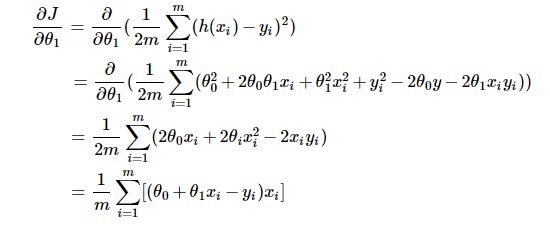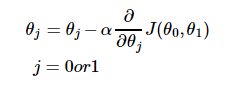在统计学中,线性回归(英语:linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归(multivariate linear regression)。——————维基百科
长久以来,这部分内容都是ML的敲门砖,吴恩达教授在他的课程中也以此为第一个例子,同时,本篇也参考了许多吴教授的内容。
在这里,我简单把自变量称为x,因变量称为y。在单变量线性回归中,x是一个一维的连续值。
单变量线性回归即是为所给数据,拟合一个最优方程,也就是划出一条最符合原始数据的线(通常要求数据为连续值)。
在本篇,我们将用梯度下降的方法,拟合出一条与原始数据最接近的直线,换言之,找到拟合效果最好的直线方程。
假设设直线方程如下:
![]() (θ0即是常数项,或者说是一个常数偏移值)
(θ0即是常数项,或者说是一个常数偏移值)
在学习梯度下降法之前,我们还需要了解一些前缀知识,包括但不限于:
-
归一化(数据预处理)
归一化公式:
归一化是一种把数据映射到[0, 1]区间内的预处理,在本例中,这样处理主要是为了提高梯度下降收敛的速度。
-
cost 函数
cost函数(function)是一个评估回归模型是否拟合得好的函数,cost越低的函数,说明模型拟合数据集越好。
在本例中,采用了比较常用的方差,即
-
梯度 (gradient)以及迭代项的推导
梯度是函数在变化最快的方向上的方向导数,它是偏导的一种应用(这部分知识可参考微积分或高等数学内容,虽然即使不了解也可直接使用推论,但如果想深入学习的话还是吃透为好)。按梯度的定义可知:
这部分是对θ1的偏导,对θ0的偏导可自行推导,与以上差别不大。若有疑惑(为什么对cost 函数求偏导?),请往下看。
了解完以上内容后,我们知道,对于给定的θ1和θ0,我们凭借cost 函数就能评估出他们的好坏(cost越小,拟合越好)。同时,我们知道不论对于θ1/0来说,必然存在某个最准确、拟合效果最好的值,一旦偏离这个值,偏离得越远,拟合效果就越差,cost 函数的值也就越大。
假设θ0恒为0,那么cost关于θ1的函数的图像应当为一个类似山谷的形状,如下图:
最低点即使拟合最好的θ1(cost最小)。
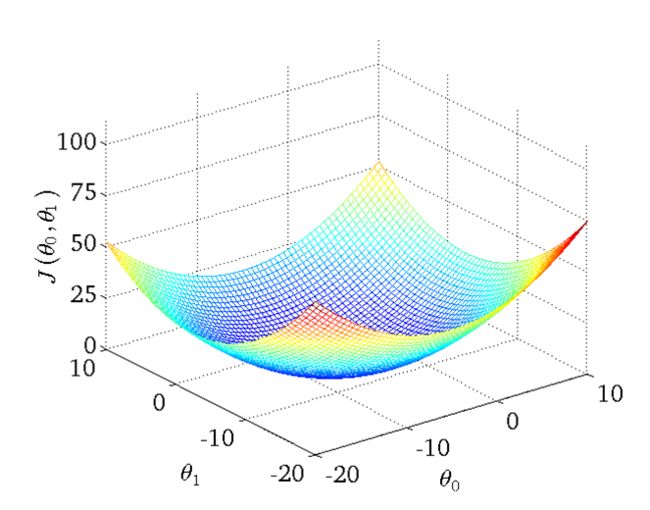
同理,假设θ0不恒定,那么图像将有两个自变量,形状大致像一个碗,如下图:
易得,在‘碗’的最低点(θ0', θ1')即是拟合效果最好的θ0与θ1,那么如何找到这个最低点呢?
梯度下降是这么认为的,首先随机取一个点,然后按梯度方向去迭代点,让点越来越趋近、直至收敛于最低点。
原理很简单,但是这个迭代公式该如何求呢?
答案也不难,就是按照梯度的概念来:
几何意义大抵是点(θ0,θ1)以α为速率,梯度为步长,按梯度方向(函数变化最快的方向)向最低点移动。
伪代码:
① 随机初始化点
② 按照一定的比例/步伐(学习率),往梯度向下的方向迭代
③ 收敛或精度足够时停止
可能有的人不太懂收敛的原因,这部分涉及到微积分的知识,大致是这样:
当点越趋近最低点时,偏导会越来越小,直至为0,此时收敛。可以认为在接近最低点的过程中,切向量的值逐渐减小(碗状曲面逐渐平缓),抵达最低点时,切平面平行于xoy面,切向量为0,此时不论如何迭代,θ的值都不再变化。
我们知道,前面的原理部分并没有涉及到α学习率(learning rate)这个概念,那么这个东西是要干什么呢?
看过吴教授课程的同学可能知道,在下降的过程中,如果步伐太大的话,是无法收敛到最低点的,如果不加上α来控制步伐大小,在很多情况下,都可能导致无法找到最低点。
为了解决这个问题,梯度下降引入了α来控制下降的步伐大小,确保能够收敛。但同时,α太小的话,也会导致收敛过慢。
需要着重说明的是θ1和θ2应该严格同步更新,按我的理解来,这是因为梯度是基于当前点的最大变化值,如果异步更新的话,比方说我们先更新θ1,然后再遍历更新θ0,此时更新θ0是基于新的θ1,所以不满足梯度的要求。
顺带一提,梯度下降总会收敛于局部最小值。不过在单变量线性回归中,局部最小值即是全局最小值。
以上就是单变量线性回归的内容,接下来我们将尝试应用于数据集:
给出一个数据集(工作经验与年薪)如下:
YearsExperience |
Salary |
1.1 |
39343.00 |
1.3 |
46205.00 |
1.5 |
37731.00 |
| .... | .... |
文末将给出下载地址。
首先对数据进行归一化,提高收敛速度。然后我们简单地设置θ初始值为(0,0),α为0.01,精度为1e-4,最大迭代次数为1e4。
拟合效果如下:
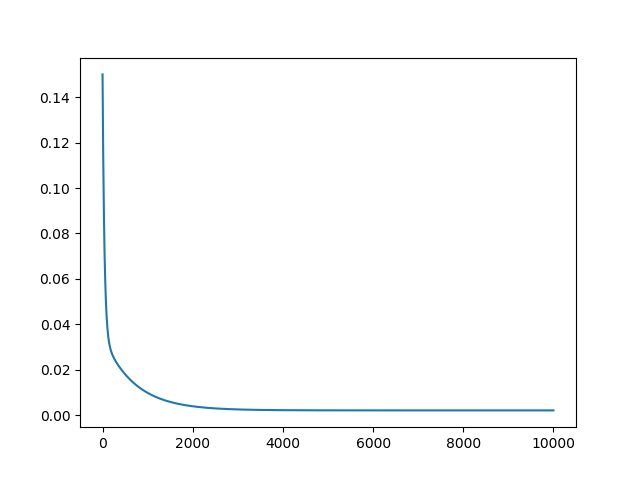
可以看到效果还是比较理想的,接下来是cost的变化图像:
可以看到大致迭代3000次的时候基本收敛了,由于收敛值大于精度,所以迭代次数为设置的最大次数。
总结:
这部分内容应该说相当好上手,主要把握好梯度这个概念,理解好迭代(逐渐趋于cost局部最小),之后就都不难了。并且梯度下降在机器学习中有比较广泛的应用,所以对它的学习必不可少。
数据集和代码我都推到github上了,有需要请点击:https://github.com/foolishkylin/workspace/tree/master/machine_learning/getting_started/gradient_descent/liner_regression_single