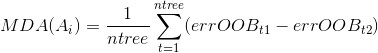用通俗易懂的方式剖析随机森林
0.引言
随机森林是现在比较流行的一个算法。对于回归和分类问题有很好的效果,它的内在的机理到底是什么呢?接下来将会用通俗易懂的方式讲一讲随机森林。
1.什么是随机森林
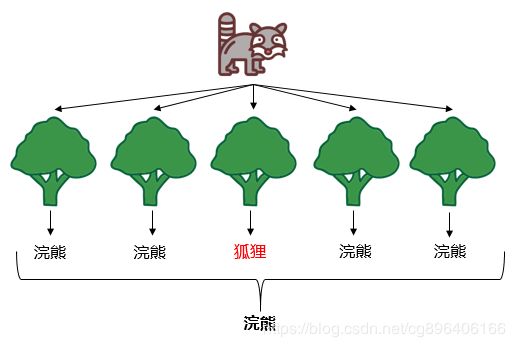
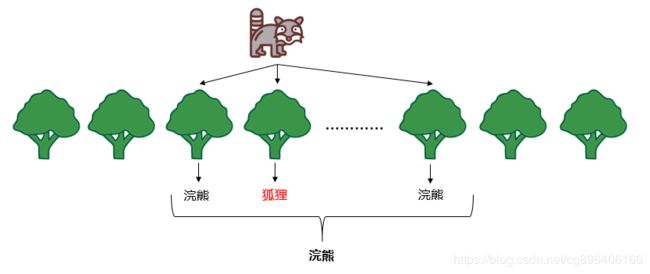
随机森林分解开来就是“随机”和“森林”。“随机”的含义我们之后讲,我们先说“森林”,森林是由很多棵树组成的,因此随机森林的结果是依赖于多棵决策树的结果,这是一种集成学习的思想。森林里新来了一只动物,森林举办森林大会,判断这到底是什么动物,每棵树都必须发表意见,票数最多的结果将是最终的结果。随机森林最终的模型见下图示:
森林中的每棵树是怎么构建出来的,是不是每棵树都是判断正确的树,这是我们需要考虑的一些问题。接下来我们就来看一看森林中的每棵树是怎么来的?怎么选出“优秀”的树?
1.如何构建一棵树
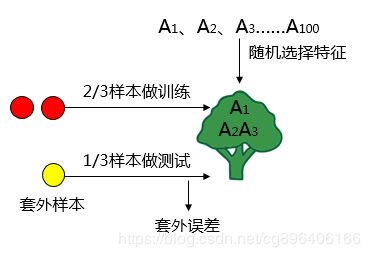
假设共有个样本,M个特征。 这里我们讲“随机”的含义。对于每棵树都有放回的随机抽取训练样本,这里抽取随机抽取的样本作为训练集,再有放回的随机选取个特征作为这棵树的分枝的依据,这里要注意。这就是“随机”两层含义,一个是随机选取样本,一个是随机选取特征。这样就构建出了一棵树,需要注意的是这里生成的树都是完全生长的树(关于为什么是要完全生长的树,我认为的原因是便于计算每个特征的重要程度,剪枝的话将无法进行计算,一棵树的构建方式如下图所示:
按照这种方法,可以构建出很多棵树,那么这么多棵树综合评判的结果可以作为最后的结果吗?
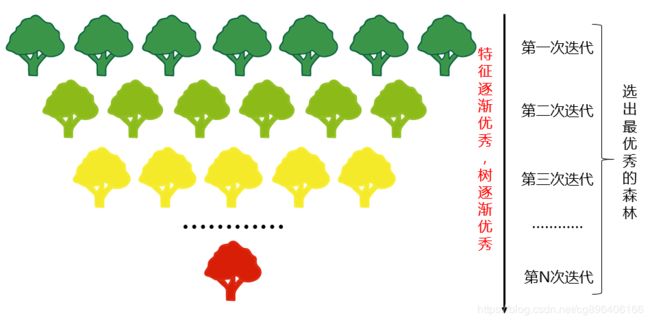
当然不是的,随机森林真正厉害的地方不在于它通过多棵树进行综合得出最终结果,而是在于通过迭代使得森林中的树不断变得优秀(森林中的树选用更好的特征进行分枝)。上面的一个森林相当于第一次迭代得到的森林。那么随机森林是怎么往后迭代的呢?
2.如何选出优秀的特征
随机森林的思想是构建出优秀的树,优秀的树需要优秀的特征。那我们需要知道各个特征的重要程度。 对于每一棵树都有个特征,要知道某个特征在这个树中是否起到了作用,可以随机改变这个特征的值,使得“这棵树中有没有这个特征都无所谓”,之后比较改变前后的测试集误差率,误差率的差距作为该特征在该树中的重要程度,测试集即为该树抽取样本之后剩余的样本(袋外样本)(由袋外样本做测试集造成的误差称为袋外误差)。 在一棵树中对于个特征都计算一次,就可以算法个特征在该树中的重要程度。我们可以计算出所有树中的特征在各自树中的重要程度。但这只能代表这些特征在树中的重要程度不能代表特征在整个森林中的重要程度。那我们怎么计算各特征在森林中的重要程度呢?每个特征在多棵数中出现,取这个特征值在多棵树中的重要程度的均值即为该特征在森林中的重要程度。如下式:
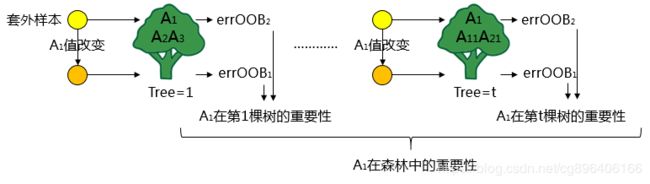
其中表示特征在森林中出现的次数。表示第棵树中属性值改变之后的袋外误差,表示第棵树中正常值的袋外误差。可以用下图来表示:
这样就得到了所有特征在森林中的重要程度。将所有的特征按照重要程度排序,去除森林中重要程度低的部分特征,得到新的特征集。这时相当于我们回到了原点,这算是真正意义上完成了一次迭代。
3.如何选出最优秀的森林
按照上面的步骤迭代多次,逐步去除相对较差的特征,每次都会生成新的森林,直到剩余的特征数为为止。最后再从所有迭代的森林中选出最好的森林。迭代的过程如下图所示:
得到了每次迭代出的森林之后,我们需要选择出最优秀的森林(随机森林毕竟是集成学习,所以最后的森林不一定是最优的。
那么我们怎么比较这些森林的好坏呢?这时我们需要引入一个指标来评价一个森林的好坏,上面的用于评价套外样本在树中的误差率,这里的评价套外样本在森林中的误差率。(因为都是利用套外样本,所以名字都是(out-of-bag)) 每个样本在多棵树中是套外样本,通过多棵树的预测这个样本的结果。预测方式如下图所示:
预测出所有所有样本的结果之后与真实值进行比较,就可以得到这个森林的套外误差率。
选择套外误差率最小的森林作为最终的随机森林模型。
以上就是我对随机森林的理解,希望可以帮助到大家。