NBER:一个简单的计划隔离问题 | 唧唧堂论文解析
picture from Internet
专栏介绍
![]()
长按二维码直接进入专栏
本文为唧唧堂《新冠病毒主题论文导读专栏》内一篇论文解析,唧唧堂将在本专栏收录发布所有新冠病毒主题的经济金融社会心理等社科类论文解析导读,同时也或将收录部分医学论文。
本专栏论文收录无截止时限,现已有超100篇NBER工作论文解析中,未来唧唧堂将源源不断把发现的新冠病毒主题论文放入本专栏,期待各位研究人的关注与订阅。点击了解专栏!
唧唧堂现招募更多经济金融研究人加入写作小组,以更快完成本专栏内容的解析产出,解析作者在获得固定稿费同时,还将获得付费阅读收入的部分提成。点击加入写作小组!
本文是针对工作论文《A Simple Planning Problem for COVID-19 Lockdown(一个简单的计划隔离问题)》的一篇解析(NBER Working Paper 26981)。该论文作者是Fernando E. Alvarez, David Argente,和Francesco Lippi。该论文基于广泛采用的传染病模型(SIR),站在社会计划者(social planner)的角度,试图在隔离的成本与(可能发生的)患病死亡造成的损失之间做出权衡,以探索一条最优的隔离-时间路径。
研究背景与问题
生命诚可贵,工作价更高?今年COVID-19在世界范围的爆发使得我们观察到了各国政府采取的不同应对策略及其迥然不同的疫情发展。当各国政府在制定譬如隔离(social distancing)或封城(lockdown)策略时,无外乎是在“工作”和“生命”之间做出权衡。换言之,其实是在两种经济成本之间做出权衡:一方面隔离的严厉程度与生产部门受到的影响正相关,从而产生经济成本;另一方面,隔离的严厉程度又跟疫情的发展密切相关,尤其是易感人群(the Susceptible,简称S)未来患病的可能性——一旦患病,易感人群则会遭受患病(或死亡)造成的(数学期望意义上的)经济损失。因此,社会计划者必须通过为疫情中的每个时间点选择合适的隔离程度,从而最大化未来所有效用(比如GDP)的现值。笔者认为,此论文的主要贡献在于考虑了内生康复率和康复者的可识别性。
模型
要解决上述问题,必须要找到社会计划者的目标函数;要写出该目标函数,就必须搞清楚疫情传播的动态。因此本文的模型分为两部分,一是用于研究疫情传播动态的传染病模型,二是权衡隔离成本与感染损失的目标函数。
1、传染病模型(Susceptible-Infected-Recovered, SIR)
传染病模型虽然是研究此类问题的经典范式,但实际构建则要依赖于目标函数的具体要求。比如此论文将隔离成本定为被隔离的那部分人“本来可以”生产的产出价值(output);患病损失定义为患病死亡的那些人未来“(一辈子)本来可以”生产的总产出的现值。因此,在传统的易感(S)-患病(I)-康复(R)三状态划分人群的基础上,此模型还需要考虑死亡(D),也就是说随着疫情传播,总人数会减少。
和传统类似,本文中疫情的动态变化也可以表示为一个微分方程组,如下所示:
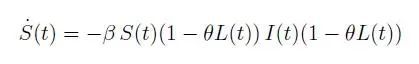
其中,S是易感人群,I是患病人群,D是死亡人群(都以比例来表示),N(t) = S(t) + I(t) + R(t),也就是系统生存者的比例。这三行方程依次表示S、I、N(或D)的动态变化,而由于R在这个模型中不太重要,并且其变化可以由N-S-I来说明,故略去。直观来说,S通过在系统中与I自由接触而感染,感染速率为β,而L(t)表示t时刻的隔离程度(此模型中表示选择L比例的人群来绝对隔离,例如,L=0.6表示随机选择总人群N中60%的人来隔离),介于0和1之间——如果完全不隔离,S减少(感染)的速率即为βSI,相当于感染速率乘以系统中S和I碰面的几率。此处θ是隔离的“效果”,也就是说隔离政策降低S与I接触的程度,介于0和1之间——如果θ=1,则隔离是完全有效的,被隔离的人完全不能与被感染者接触;然而,θ<1更符合现实情况。
S被感染之后(减少)就变成了I(增加),这也就解释了I动态变化(第二行方程)中的第一项。至于第二项-γI,则是单位时间由患病转为康复的人群,γ是康复速率。然而实际上I的动态变化的最后应该加上一项 “-Φ(I(t))I(t)”,这部分是单位时间由患病而死亡的人群,其中Φ(I(t))是一个与I有关的死亡速率。至此,也就不难看出为什么第三行方程写作上述形式了。给定一组合理的初值(N(0)=1, S(0), I(0)),给定一个合理的隔离路径L(t),这个传染病模型就能输出整个疫情中各状态人群的动态变化。
此处作者将死亡速率Φ(I(t))内生化(在解模型的过程中被作者简化为Φ(I)=+κI ,关于I线性),其实是一个颇为合理的假设。在疫情期间,我们往往看见很多国家和地区的医疗资源发生“挤兑”现象,即I越大,医疗资源不足的风险就越高,从而导致患病者得不到救治,即死亡率越高。虽然此处死亡速率与I的关系应该比线性更高阶(有可能是指数关系),但即便是线性的关系,作者也发现了内生和外生死亡率所造成的显著不同,也不失为一个有效的尝试。
2、目标函数及其组成部分
假设疫情系统中处于生存状态且没有被隔离的人单位时间内能产生w的产出价值,并且假设每个人的寿命是无限的,除非她因感染而死亡。除此之外,假设计划者的折现率为r,而ν为每一时间点特效药和疫苗一起出现的概率(一旦出现,则所有感染者I都被治愈,而所有易感者S都产生免疫)。至此,社会计划者想要最大化的目标函数可以被表示如下:
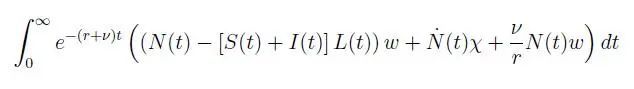
而社会计划者的控制量只有L(t)。这个目标函数相当于是未来所有时期社会总产出的现值。从大括号里的第一项可以看出,在某个时期t,如果L(t) = 0 (完全不隔离),社会总产出为N(t)w;否则,隔离的那部分人的产出将被减少(基准情形中,假设康复人群R完全免疫且永远不会被隔离)。第一项除了表示产出价值之外,实际上也隐含了死亡的机会成本——如果有一定比例的人死亡,N(t)会变小,从而社会在某一时刻所能达到的总产出也会变小。大括号里的第二项是对死亡成本的进一步校正,因为人死亡对社会产生的代价可能远不只是她这辈子少赚了那么多钱而已。最后一项表示每一时刻都有ν的概率让疫情瞬间结束,自那以后所有人都可以出来正常工作所带来的总收益的现值。
以上,我们已经正式建立了整个模型,而解这个模型不过是一个最优控制问题——控制L(t)使得目标函数最大化,而目标函数里面的状态量服从SIR传染病模型的动态变化。
其他假设
为了使模型更贴近现实或使模型更易于驾驭,作者们采取了其他一些重要假设:
(1) 假设隔离程度的上限小于或等于1——实际上即使最严厉的隔离措施也必须要维持一些重要部门的运转,比如医疗健康、食物生产、交通运输等。
(2) 基准情形考虑隔离效果θ= 0.5,且能够识别康复者R(τ=1,从而不用对R进行无谓的隔离)。但后面的比较分析中探究了不能识别康复者R(τ=0)的情况。
(3) 假设感染状态且没有被隔离的人群仍能按原来的效率w来生产产出(不太现实)。
