[请参阅http://zh.wikipedia.org/wiki/%E6%AD%A3%E4%BA%A4%E5%9D%90%E6%A8%99%E7%B3%BB,如果没有被墙的话……]
直角坐标、极坐标、柱坐标和球坐标这几种坐标系都是正交坐标系,证明似乎并不麻烦(没证明过,想象了一下);当我们将直角坐标系下的积分变换到其他坐标(或者更灵活一点,随便变来变去),并将其他坐标也画成正交的形式(比如极坐标的r和Θ),那么经过变换后的图形是不一样的。例如直角坐标下圆心在原点的圆弧变换到极坐标下就变成了线段(r固定)。由此可以想象,当进行积分运算的时候,大概就要对被积函数乘以一个因子,这个因子就是雅克比行列式的绝对值。
直角坐标下,梯度grad(f)=df/dxax+df/dyay+df/dzaz
df=df/dx·dx+df/dy·dy+df/dz·dz=grad(f)·dl
圆柱坐标下,可以用类似的方法得到梯度表达式:
df=df/dr·dr+df/dφ·dφ+df/dz·dz=grad(f)·dl
dl=drar+rdφaφ+dzaz
于是grad(f)就有了。
圆柱和球坐标下的散度和旋度:使用向量运算恒等式将散度和旋度转换为梯度运算。见第一行。
梯度场的旋度为0;
旋度场的散度为0。
梯度场总是指向函数增长最快的方向。
旋度的散度为零,意味着一个散度场任意叠加上一个有旋场不会改变其散度,也就是说光凭矢量场的散度无法唯一地确定这个矢量场。而光凭矢量场的旋度也无法唯一地确定这个矢量,这是因为有旋场可以叠加上这么一个矢量场而不改变其旋度,而这个矢量场是一个标量函数的梯度。
向量旋度并*不*表示向量“”形态”是否是“旋转”的。例如,无限长直导线周围*不*包含导线的区域形态似乎是“旋转”的,但其旋度为0。(不过从另一个角度来说,只要所取区域不包含导线,沿磁力线方向就没办法从起点旋转回来。因此,具有旋转形态但旋不回来的向量旋度为0?)
旋度是环量(矢量场绕闭合路径的线积分)的度量。仍以无限长直导线周围的磁场为例,空间任一点磁通密度沿周围的无限小闭合路径的线积分为0:设该闭合路径垂直于z轴,四边分别沿ρ和φ,那么两条沿ρ的边积分为0,两条沿φ的边积分反向所以和为0。
在计算向量场的散度或旋度时,将x,y,z看做独立变量:因为在向量场的表达式中它们就是独立变量啊。
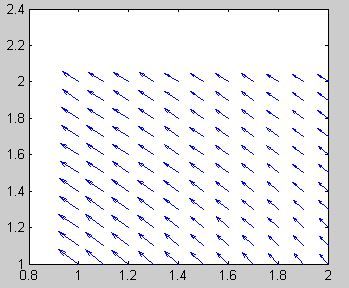
下面演示使用Matlab画出一个向量场M=-y/(x2+y2),N=x/(x2+y2)
>> [x,y]=meshgrid(1 : .1 : 2 , 1 : .1 : 2);
>> M=-y./(x.*x+y.*y);
>> N=x./(x.*x+y.*x);
>> quiver(x,y,M,N);
这是一个无旋场。
如果你想看有旋场,可以用下面这个向量:
M=-y
N=x