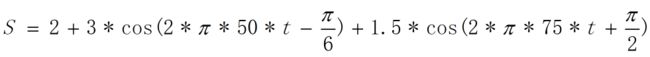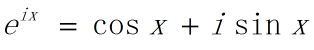2019独角兽企业重金招聘Python工程师标准>>> ![]()
一. 简介
离散傅里叶变换(Discrete Fourier Transform, DFT)是数字信号处理最重要的基石之一,也是对信号进行分析和处理时最常用的工具之一。在200多年前法国数学家、物理学家傅里叶提出后来以他名字命名的傅里叶级数之后,用DFT这个工具来分析信号就已经为人们所知。但在很长时间内,这种分析方法并没有引起更多的重视,最主要的原因在于这种方法运算量比较大。
快速傅里叶变换(Fast Fourier Transform, FFT)是1965年由库利(T.W.Cooley)和图基(J.W.Tukey)共同提出的一种快速计算DFT的方法。这种方法充分利用了DFT运算中的对称性和周期性,从而将DFT运算量从N2减少到N*log2N。当N比较小时,FFT优势并不明显。但当N大于32开始,点数越大,FFT对运算量的改善越明显。比如当N为1024时,FFT的运算效率比DFT提高了100倍。
在库利和图基提出的FFT算法中,其基本原理是先将一个N点时域序列的DFT分解为N个1点序列的DFT,然后将这样计算出来的N个1点序列DFT的结果进行组合,得到最初的N点时域序列的DFT值。实际上,这种基本的思想很早就由德国伟大的数学家高斯(1777年4月30日-1855年2月23日)提出过,只是由于当时尚欠东风——计算机还没发明。在20世纪60年代,伴随着计算机的发展和成熟,库利和图基的成果掀起了数字信号处理的革命,因而FFT发明者的桂冠才落在他们头上。
库利和图基的FFT算法的最基本运算为蝶形运算,每个蝶形运算包括两个输入点,因而也称为基-2算法。在这之后,又有一些新的算法,进一步提高了FFT的运算效率,比如基-4算法、分裂基算法等。这些新算法对FFT运算效率的提高一般在50%以内,远远不如FFT对DFT运算的提高幅度。从这个意义上说,FFT算法是里程碑式的。可以说,正是计算机技术的发展和FFT的出现,才使得数字信号处理迎来了一个崭新的时代。
只有周期信号可以通过傅里叶变换分解,随机信号、无规则信号是不能分解的。
二. FFT(Matlab角度分析)
现举例:
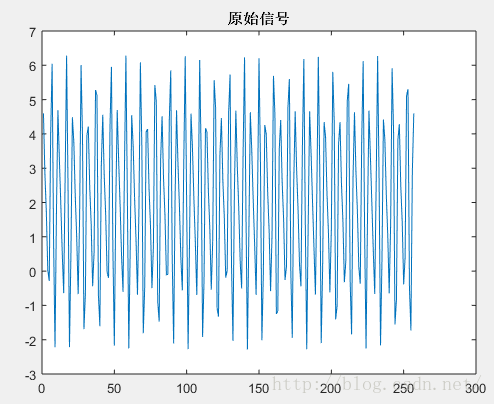
假设我们有一个信号(如图一所示),它是一个与时间无关的常数。
它含有
①2V的直流分量(注:信号的直流分量就是信号的平均值),
②频率为50Hz、相位为-30度、幅度为3V的交流信号,
以及一个
③频率为75Hz、相位为90度、幅度为1.5V的交流信号。
用数学表达式就是如下:
![]()
式中cos参数的单位为弧度,所以-30度和90度要分别换算成弧度,即各除以180。换算后,是:
拓展:
傅里叶级数的物理意义很明确:把一个周期信号表示为一系列不同频率的复指数信号的线性组合。上公示:
注意,这个公式的最小组成单位是复指数(复数指数)信号,也就是这个:
(
拓展:欧拉公式,对任意实数x,都存在
其中e是自然对数的底数,i是虚数单位,而cos和sin则是余弦、正弦对应的三角函数,参数x则以弧度为单位。
)
我们知道,复指数信号不是实信号,它在现实中是不存在的,因为它带有虚部i。
那如何用复指数信号合成实信号呢?
答案很简单:只要两个复数共轭就好,实部相加,虚部相抵。也就是欧拉公式:

所以我们在用傅里叶级数分析信号的时候,频谱绝对是对称的,用很多对指数相反的复指数信号,就可以合成实信号,也就是说:有k,则必然有-k,否则无法合成实信号。
综上,出现负频率的根本原因就是傅里叶级数(变换)的最小单位是复指数信号,如果用傅里叶级数的另一种形式,把信号表示为一系列正余弦信号的组合,就不存在负频率了。
至于形象的理解,可以看那个帖子的第一页,有图很容易理解。
倍频?
这个解释起来比较简单,采样的过程其实就是周期采样信号乘以模拟信号。
最终采样之后的信号的频谱就是这样,形成了频谱的延拓,这就是题主说的倍频吧。
例子:
图一
式中cos参数为弧度,所以-30度和90度要分别换算成弧度。我们以256Hz的采样(频)率对这个信号进行采样,总共采样256点。按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第n个点的频率就是n-1。我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第51个点、第76个点上出现峰值,其它各点应该接近0。实际情况如何呢?我们来看看FFT的结果的模值如图所示。
图二 FFT结果
从图中我们可以看到,在第1个采样点、第51个采样点、和第76个采样点附近有比较大的值。我们分别将这三个点附近的数据拿上来细看:
1点: 512+0i
2点: -2.6195E-14 - 1.4162E-13i
3点: -2.8586E-14 - 1.1898E-13i
50点:-6.2076E-13 - 2.1713E-12i
51点:332.55 - 192i
52点:-1.6707E-12 - 1.5241E-12i
75点:-2.2199E-13 -1.0076E-12i
76点:3.4315E-12 + 192i
77点:-3.0263E-14 +7.5609E-13i
很明显,1点、51点、76点的值都比较大,它附近的点值都很小,可以认为是0,即在那些频率点上的信号幅度为0。接着,我们来计算各点的幅度值。分别计算这三个点的模值,结果如下:
1点: 512
51点:384
76点:192
按照公式,可以计算出:
直流分量为:512/N=512/256=2;
50Hz信号的幅度为:384/(N/2)=384/(256/2)=3;
75Hz信号的幅度为192/(N/2)=192/(256/2)=1.5。
可见,从频谱分析出来的幅度是正确的。
然后再来计算相位信息。直流信号没有相位可言,不用管它。先计算50Hz信号的相位,atan2(-192, 332.55)=-0.5236,结果是弧度,换算为角度就是180*-0.5236)/pi=-30.0001。再计算75Hz信号的相位,atan2(192, 3.4315E-12)=1.5708弧度,换算成角度就是180*1.5708/pi=90.0002。可见,相位也是对的。根据FFT结果以及上面的分析计算,我们就可以写出信号的表达式了,它就是我们开始提供的信号。
总结:假设采样频率为Fs,采样点数为N,做FFT之后,某一点n(n从1开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以N/2就是对应该频率下的信号的幅度(对于直流信号是除以N);该点的相位即是对应该频率下的信号的相位。相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi到pi。要精确到xHz,则需要采样长度为1/x秒的信号,并做FFT。要提高频率分辨率,就需要增加采样点数,这在一些实际的应用中是不现实的,需要在较短的时间内完成分析。解决这个问题的方法有频率细分法,比较简单的方法是采样比较短时间的信号,然后在后面补充一定数量的0,使其长度达到需要的点数,再做FFT,这在一定程度上能够提高频率分辨力。具体的频率细分法可参考相关文献。
[附录:本测试数据使用的matlab程序]
close all; % 先关闭所有图片
Adc=2; % 直流分量幅度
A1=3; % 频率F1信号的幅度
A2=1.5; % 频率F2信号的幅度
F1=50; % 信号1频率(Hz)
F2=75; % 信号2频率(Hz)
Fs=256; % 采样频率(Hz)
P1=-30; % 信号1相位(度)
P2=90; % 信号2相位(度)
N=256; % 采样点数
t=[0:1/Fs:N/Fs]; % 采样时刻
% 信号
S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180);
% 显示原始信号
plot(S);
title('原始信号');
figure;
Y = fft(S,N); % 做FFT变换
Ayy = (abs(Y)); % 取模
plot(Ayy(1:N)); % 显示原始的FFT模值结果
title('FFT 模值');
figure;
Ayy=Ayy/(N/2); % 换算成实际的幅度
Ayy(1)=Ayy(1)/2;
F=([1:N]-1)*Fs/N; % 换算成实际的频率值
plot(F(1:N/2),Ayy(1:N/2)); % 显示换算后的FFT模值结果
title('幅度-频率曲线图');
figure;
Pyy=[1:N/2];
for i=[1:N/2]
Pyy(i)=phase(Y(i)); % 计算相位
Pyy(i)=Pyy(i)*180/pi; % 换算为角度
end;
plot(F(1:N/2),Pyy(1:N/2)); % 显示相位图
title('相位-频率曲线图');Matlab的实验结果如下:
看完这个你就明白谐波分析了。
三. FFT(数学角度分析)
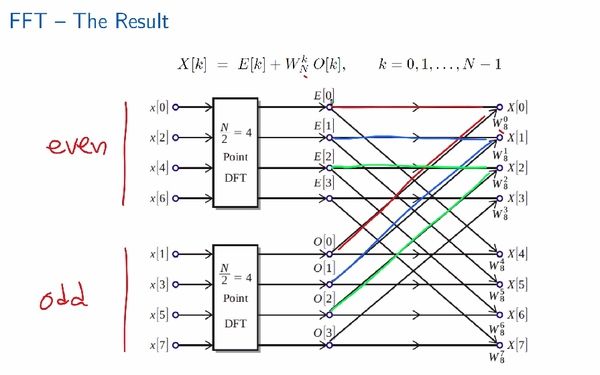
FFT的具体计算过程可以通过蝶形图可视化:
第一次分解:
第二次分解:
第三次分解:
FFT与DFT的性能比较:
除了运算效率的大幅度提高外,FFT还大大降低了DFT运算带来的累计量化误差,这点常为人们所忽略。