机器学习——模型评估

前言

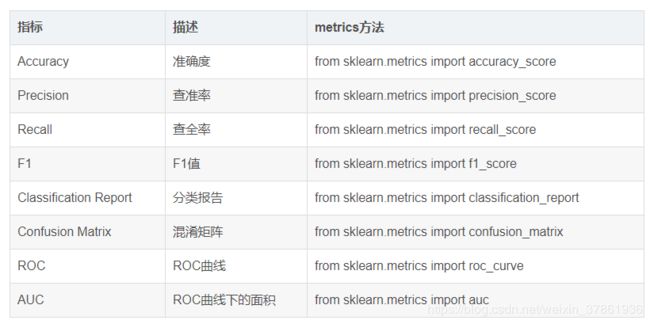
当创建好一个机器学习模型之后，我们需要评估这个模型的性能好坏，以确定模型是否可用，在sklearn中的metrics模块提供了各种模型评估方法。
对分类模型和回归模型，我们需要使用不同的方法对模型进行评估。

1、分类模型评估

对于分类模型，主要有以下几种评估指标：

• 准确率（accuracy）

正确分类的样本数占所有样本数的比例
$$accuracy=\frac{n_{correct}}{n_{total}}$$
$n_{correct}$:被正确分类的样本个数
$n_{total}$:总样本的个数
准确率的局限性:
准确率是分类问题中最简单也是最直观的评价指标，但存在明显的缺陷，当不同种类的样本比例非常不均衡时，占比大的类别往往成为影响准确率的最主要因素。比如：当负样本占99%,分类器把所有样本都预测为负样本也可以得到99%的准确率，换句话说总体准确率高，并不代表类别比例小的准确率高。
代码展示：

from sklearn.metrics import accuracy_score
y_true = [0, 1, 1, 1, 1]
y_pred = [0, 0, 1, 1, 1]
accuracy_score(y_true=y_true,y_pred=y_pred)

运行结果为：0.8

• 查准率（precision）和查全率（recall）
  
  图片来源于：https://www.jianshu.com/p/4434ea11c16c

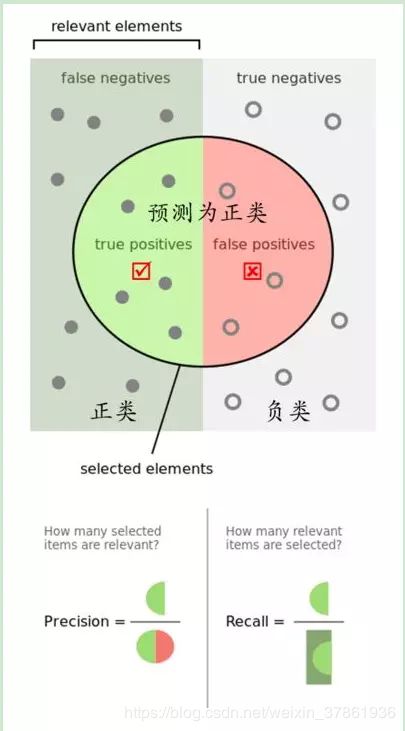
查准率是指正确分类的正样本个数占分类器判定为正样本的样本个数的比例
$$precison=\frac{TP}{TP+FP}$$
查全率是指正确分类的正样本个数占真正的正样本数的比例
$$recall=\frac{TP}{TP+FN}$$

代码展示：

from sklearn.metrics import precision_score,recall_score
print(precision_score(y_true=y_true,y_pred=y_pred))
print(recall_score(y_true=y_true,y_pred=y_pred))

运行结果1.0 #查准率 0.75#查全率

• F1值（F1_score）

从数学上来看，F1值其实是查准率与查全率的调和平均数，综合考虑了查全率和查准率，是一个比较好的评估指标

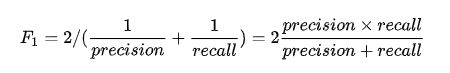
代码展示：

from sklearn.metrics import f1_score
f1_score(y_true=y_true,y_pred=y_pred)

运行结果：0.8571428571428571

• 分类报告（classification Report）

综合提供了查准率（precision）、查全率（recall）和F1值三种评估指标

代码展示

from sklearn.metrics import classification_report
print(classification_report(y_true=y_true,y_pred=y_pred))

运行结果：

                precision    recall  f1-score   support

           0       0.50      1.00      0.67         1
           1       1.00      0.75      0.86         4

    accuracy                           0.80         5
   macro avg       0.75      0.88      0.76         5
weighted avg       0.90      0.80      0.82         5

• 混淆矩阵（Confusion Metrics）

混淆矩阵是一个N X N矩阵，N为分类的标签个数。假如我们面对的是一个二分类问题，则N＝2，我们就得到一个2 X 2矩阵。

代码展示：

from sklearn.metrics import confusion_matrix
print(confusion_matrix(y_true=y_true,y_pred=y_pred))

运行结果为：

[[1 0]
 [1 3]]

• ROC曲线

ROC曲线其实就是从混淆矩阵衍生出来的图形，其横坐标为Specificity，纵坐标为Sensitivity。
Specificity=FPR(False positive rate)，即假正类率，预测为正但实际为负的样本占所有负例样本的比例。
Sensitivity=TPR(True positive rate)，即是真正类率，预测为正且实际为正的样本占所有正例样本的比例。
如下是一个ROC曲线示例：

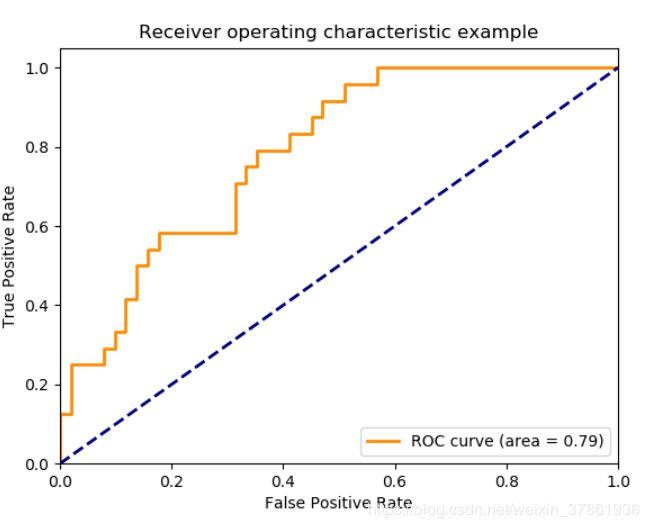
在一个二分类模型中，假设采用逻辑回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如0.6，概率大于等于0.6的为正类，小于0.6的为负类。对应的可以算出一组(FPR,TPR)，在平面中得到对应坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。阈值最大时，对应坐标点为(0,0)，阈值最小时，对应坐标点(1,1)。

理想目标：TPR=1，FPR=0，即图中(0,1)点，故ROC曲线越靠拢(0,1)点，越偏离45度对角线越好。

• AUC

AUC (Area Under Curve) 被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围一般在0.5和1之间。

使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，AUC越大，分类器效果更好。

使用AUC判断分类器优劣的标准：

1. AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
2. 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
3. AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
4. AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

为什么要使用ROC曲线和AUC？
当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。在这种情况下，查全率和查准率会有较大的波动。

2、回归模型评估

对于回归模型，主要有以下几种评估指标：

指标	描述	sklearn 函数
Mean Square Error (MSE, RMSE)	平均方差、均方根误差	from sklearn.metrics import mean_squared_error
Absolute Error (MAE, RAE)	绝对误差	from sklearn.metrics import mean_absolute_error, median_absolute_error
R-Squared	R平方值	from sklearn.metrics import r2_score

• 平均方差MSE

计算公式：$MSE=\frac{1}{m}\sum _{i=1}^m({\hat{y}}_i-y_i{)}^2$
线性回归的损失函数,是最常用的回归模型评估指标

• 均方根误差RMSE

计算公式:$RMSE=\sqrt{MSE}$
RMSE能够很好地反映回归模型预测值与真实值的偏离程度

• 绝对误差MAE

是绝对误差的平均值，能更好地反映预测值误差的实际情况
计算公式：$MSE=\frac{1}{m}\sum _{i=1}^m|{\hat{y}}_i-y_i|$

• R平方值
  计算公式：
  $$R^2=1-\frac{\sum _{i=1}^m(\widehat{y_i}-y_i{)}^2}{\sum _{i=1}^m(y_i-\bar{y}{)}^2}$$
  残差平方和：$\sum _{i=1}^m(\widehat{y_i}-y_i{)}^2$
  方差：$\sum _{i=1}^m(y_i-\bar{y}{)}^2$

当$R^2$越接近1，我们认为模型拟合效果越好

参考链接：
https://www.jianshu.com/p/c61ae11cc5f6
https://www.jianshu.com/p/c4e24a6a9633
https://www.cnblogs.com/zingp/p/10612558.html#_label14