(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks
计划完成深度学习入门的126篇论文第二十一篇,DeepMind研究一种新的生成模型。
ABSTRACT&INTRODUCTION
摘要
自然图像的分布建模是无监督学习中的一个标志性问题。该任务需要一个同时具有表现力、可处理性和可伸缩性的图像模型。我们提出了一种深度神经网络,它能在两个空间维度上连续预测图像中的像素。我们的方法对原始像素值的离散概率建模,并对图像中的完整依赖关系进行编码。我们的结构创新包括快速的二维递归层和在深层递归网络中有效利用剩余连接(ResNet)。我们在自然图像上实现了对数似然评分,这大大优于以前的技术水平。我们的主要结果还提供了对不同ImageNet数据集的基准测试。从模型中生成的样本看起来清晰、多样且具有全局一致性。
介绍
生成图像建模是无监督学习中的一个核心问题。概率密度模型可用于各种各样的任务,从图像压缩到图像inpainting(如图1所示)和去模糊等重建形式,再到生成新图像。当模型以外部信息为条件时,可能的应用程序还包括基于文本描述创建图像或在规划任务中模拟未来帧。生成式建模的一大优点是,实际上有无穷无尽的图像数据可供学习。然而,由于图像的高维性和高度结构化,估计自然图像的分布是非常具有挑战性的。
生成模型中最重要的障碍之一是构建复杂而富有表现力的模型,这些模型也易于处理和扩展。这权衡导致了大量的生成模型,每个模型都有自己的优势。大部分工作集中于VAE s等随机潜在变量模型(Rezende et al., 2014; Kingma & Welling, 2013)这种方法旨在提取有意义的表征,但往往伴随着一个棘手的推理步骤,可能会阻碍它们的表现。
对图像中像素的联合分布进行可跟踪建模的一种有效方法是将其转换为条件分布的乘积;该方法已应用于NADE (Larochelle & Murray, 2011)和全可见神经网络(Neal, 1992; Bengio, 2000)。因子分解将联合建模问题转化为序列问题,在序列问题中,我们学习预测给定所有先前生成的像素的下一个像素。但是,要对像素与由此产生的复杂条件分布之间的高度非线性和长期相关性进行建模,就必须建立一个具有高度表达性的序列模型。
递归神经网络(RNN)是一种功能强大的模型,它提供了一系列条件分布的紧凑、共享参数化。从笔迹生成(Graves, 2013)到字符预测(Sutskever et al., 2011)再到机器翻译(Kalchbrenner & Blunsom, 2013)。二维RNN在灰度图像和纹理(Theis &Bethge,2015)。
在本文中,我们提出了二维RNNs和应用他们在大规模的自然图像模型。由此产生的像素网络由多达12个快速二维长短时记忆(LSTM)层组成。这些层在它们的状态下使用LSTM单元((Hochreiter & Schmidhuber, 1997; Graves & Schmidhuber, 2009)和采用卷积计算沿数据的空间维度之一的所有状态一次。我们设计了两种类型的图层。第一类是行LSTM层,其中沿每一行应用卷积;类似的技术描述在(Stollenga et al., 2015)。第二种类型是对角BiLSTM层,在该层中,卷积以一种新颖的方式沿图像对角线应用。网络还包括LSTM层周围的剩余连接(He et al., 2015);我们观察到这有助于训练PixelRNN达到12层的深度。
我们还考虑了第二个简化的体系结构,它与PixelRNN具有相同的核心组件。我们观察到,卷积神经网络(CNN)也可以使用掩码卷积作为具有固定依赖范围的序列模型。PixelCNN体系结构是一个完全卷积的网络,由15层组成,它保留了整个层的输入空间分辨率,并在每个位置输出一个条件分布。
PixelRNN和PixelCNN都捕捉了像素间依赖关系的全面性,而没有引入像潜在变量模型那样的独立性假设。每个像素内的RGB颜色值之间也保持依赖关系。此外,与以前将像素建模为连续值的方法(例如Theis & Bethge (2015); Gregor et al. (2014)),我们使用一个简单的softmax层实现的多项分布将像素建模为离散值。我们注意到这种方法为我们的模型提供了代表性和训练优势。
本文的贡献如下。在第三节中,我们设计了两种对应于这两种LSTM层的像素rns;我们描述了纯卷积像素cnn,这是我们最快的架构;并设计了一个多尺度的PixelRNN。在第5节中,我们展示了在我们的模型中使用离散的softmax分布和对LSTM层采用剩余连接的相对好处。接下来,我们在MNIST和CIFAR-10上对模型进行了测试,结果表明,它们获得的对数似然分数比之前的结果好得多。我们还提供了大规模的ImageNet数据集的结果调整为32 32和64 64像素;据我们所知,来自生成模型的似然值以前从未在这个数据集上报告过。最后,对像素网络生成的样本进行了定性评价。
2. Model
我们的目标是估计自然图像上的分布,该分布可用于可跟踪地计算图像的可能性,并生成新的图像。网络每次扫描一行图像,每次扫描一行中的一个像素。对于每个像素,它预测给定扫描上下文的可能像素值的条件分布。图2说明了这个过程。将图像像素上的联合分布分解为条件分布的乘积。预测中使用的参数在图像中的所有像素位置上共享。
为了捕捉生成的过程,他们需要Theis & Bethge (2015)提出使用二维LSTM网络(Graves & Schmidhuber, 2009)从左上角的像素开始,一直到右下角的像素。LSTM网络的优势在于它能够有效地处理对对象和场景理解至关重要的长期依赖关系。这种二维结构确保了信号在从左到右和从上到下的方向上都能很好地传播。
在本节中,我们首先关注分布的形式,而下一节将专门描述PixelRNN中的架构创新。
2.1. Generating an Image Pixel by Pixel
目标是为每个由n x n个像素组成的图像x分配一个概率p(x)。我们可以把图像x写成一维序列![]() 像素是逐行从图像中提取的。为了估计联合分布p(x)我们把它写成条件分布在像素上的乘积
像素是逐行从图像中提取的。为了估计联合分布p(x)我们把它写成条件分布在像素上的乘积
值![]() 为给定所有像素
为给定所有像素![]() 的第i个像素习的概率
的第i个像素习的概率![]() 。生成逐行逐像素地进行。图2(左)说明了条件设置方案。每个像素习依次由三个值共同确定,每个值对应于红色、绿色和蓝色(RGB)的颜色通道。我们将分布
。生成逐行逐像素地进行。图2(左)说明了条件设置方案。每个像素习依次由三个值共同确定,每个值对应于红色、绿色和蓝色(RGB)的颜色通道。我们将分布![]() 重写为以下公式
重写为以下公式
![]()
因此,每种颜色都取决于其他通道以及之前生成的所有像素。注意,在训练和评估过程中,像素值的分布是并行计算的,而图像的生成是顺序的。
2.2. Pixels as Discrete Variables
之前的方法对图像中的像素值采用连续分布(如Theis & Bethge (2015); Uria et al. (2014))。相比之下,我们将p(x)模型化为离散分布,方程2中的每个条件分布都是一个多项式,用softmax层建模。每个通道变量习;在这里输入256个不同的值。离散分布具有简单的表征性,并且具有任意多模态且形状无先验的优点(见图6)。实验中我们还发现,与连续分布相比,离散分布更易于学习,且具有更好的性能(第5节)。
3. Pixel Recurrent Neural Networks
在本节中,我们将描述构成PixelRNN的体系结构组件。在3.1和3.2节中,我们描述了两种类型的LSTM层,它们使用卷积来同时计算空间维度上的状态。在3.3节中,我们描述了如何结合剩余连接来改进具有多个LSTM层的PixelRNN的训练。在第3.4节中,我们描述了计算颜色离散联合分布的softmax层和确保适当调节方案的掩蔽技术。在3.5节中,我们将描述PixelCNN架构。最后,在第3.6节中,我们描述了多尺度体系结构。
3.1. Row LSTM
Row LSTM是一种单向层,它对整行图像进行从上到下的逐行处理,同时处理整行计算特性;计算是用一维卷积来完成的。对于像素![]() ,层捕获像素上方的大致三角形上下文,如图4(中心)所示。一维卷积的Kernel大小是
,层捕获像素上方的大致三角形上下文,如图4(中心)所示。一维卷积的Kernel大小是![]() 其中
其中![]() ;k的值越大,所捕获的上下文范围就越大。卷积中的权值共享保证了计算特征沿每一行的平移不变性。计算过程如下。LSTM层有一个输入到状态组件和一个重复的状态到状态组件,它们共同决定LSTM内核中的四个门。为了增强Row LSTM的并行性,首先对整个二维输入映射计算输入状态分量;对于这种情况,使用
;k的值越大,所捕获的上下文范围就越大。卷积中的权值共享保证了计算特征沿每一行的平移不变性。计算过程如下。LSTM层有一个输入到状态组件和一个重复的状态到状态组件,它们共同决定LSTM内核中的四个门。为了增强Row LSTM的并行性,首先对整个二维输入映射计算输入状态分量;对于这种情况,使用![]() 卷积来跟踪LSTM本身的行方向。卷积被屏蔽,只包含有效的上下文(见3.4节),并生成一个大小为
卷积来跟踪LSTM本身的行方向。卷积被屏蔽,只包含有效的上下文(见3.4节),并生成一个大小为![]() 的张量,表示输入映射中每个位置的四个门向量,其中h是输出特征映射的数量。为了计算LSTM层的状态到状态组件的一个步骤,我们给出了之前隐藏的和单元格状态
的张量,表示输入映射中每个位置的四个门向量,其中h是输出特征映射的数量。为了计算LSTM层的状态到状态组件的一个步骤,我们给出了之前隐藏的和单元格状态![]() ,每个状态的大小都是
,每个状态的大小都是![]() 。得到新的隐藏状态和细胞状态
。得到新的隐藏状态和细胞状态![]() :
:
其中![]() 大小为输入图的第i行
大小为输入图的第i行![]() ,
,![]() 表示卷积运算和元素相乘。权重
表示卷积运算和元素相乘。权重![]() 是状态到状态和输入到状态组件的内核权值,后者按照上面描述的方式预先计算。在输出的情况下,忘记门和输入门
是状态到状态和输入到状态组件的内核权值,后者按照上面描述的方式预先计算。在输出的情况下,忘记门和输入门![]()
![]() ,激活函数σ是logistic sigmoid函数,而对于内容门
,激活函数σ是logistic sigmoid函数,而对于内容门![]() 是双曲正切函数。每一步都立即计算输入映射的整个行的新状态。因为Row LSTM有一个三角形的接受域(图4),所以它无法捕获整个可用上下文。
是双曲正切函数。每一步都立即计算输入映射的整个行的新状态。因为Row LSTM有一个三角形的接受域(图4),所以它无法捕获整个可用上下文。
3.2. Diagonal BiLSTM
Diagonal BiLSTM设计用于并行化计算,并捕获任何图像大小的整个可用上下文。该层的两个方向以对角线的方式扫描图像,从顶部的一个角开始,到达底部的另一个角。计算中的每一步都是沿着图像中的对角线立即计算LSTM状态。图4(右)说明了计算结果和最终的接受域。
对角线的计算过程如下。我们首先将输入映射倾斜到一个空间中,这样就可以很容易地沿着对角线应用卷积。倾斜操作将输入映射的每一行相对于前一行偏移一个位置,如图3所示;
这就得到了一个大小为![]() 的映射,此时我们可以计算对角BiLSTM的输入到状态和状态到状态的分量。对于这两个方向的每一个,输入到状态的分量就是一个卷积K它构成了LSTM核心的四个门;这个运算生成一个
的映射,此时我们可以计算对角BiLSTM的输入到状态和状态到状态的分量。对于这两个方向的每一个,输入到状态的分量就是一个卷积K它构成了LSTM核心的四个门;这个运算生成一个![]() 张量。然后用一个列向卷积
张量。然后用一个列向卷积![]() 计算状态到状态的递归分量,该卷积的核大小为2x1。该步骤采用前面的隐藏状态和单元状态,结合input-to-state组件的贡献,并生成下一个隐藏状态和单元状态,如公式3所定义。然后,通过删除偏移位置,将输出特征映射倾斜回一个n n映射。这个计算在两个方向上都是重复的。给定两个输出映射,为了防止层看到未来的像素,右输出映射将向下移动一行并添加到左输出映射。
计算状态到状态的递归分量,该卷积的核大小为2x1。该步骤采用前面的隐藏状态和单元状态,结合input-to-state组件的贡献,并生成下一个隐藏状态和单元状态,如公式3所定义。然后,通过删除偏移位置,将输出特征映射倾斜回一个n n映射。这个计算在两个方向上都是重复的。给定两个输出映射,为了防止层看到未来的像素,右输出映射将向下移动一行并添加到左输出映射。
除了达到完全依赖域外,对角BiLSTM还有一个额外的优势,它使用一个卷积核,其大小为2x1,在每一步处理最少的信息,生成一个高度非线性的计算。大于2x1的内核大小并不是特别有用,因为它们没有扩展Diagonal BiLSTM的全局接受域。
3.3. Residual Connections
我们训练高达12层深度的像素。为了提高收敛速度和更直接地在网络中传播信号,我们部署了从一个LSTM层到下一个LSTM层的剩余连接residual connections(He et al., 2015)。图5显示了剩余块的关系图。PixelRNN LSTM层的输入映射具有2h特征。输入状态组件通过为每个门生成h个特征来减少特征的数量。应用递归层后,通过11 - 1卷积将输出映射上采样到每个位置的2h特征,并将输入映射添加到输出映射中。该方法与之前使用门控沿递归网络深度的方法有关(Kalchbrenner et al., 2015; Zhang et al., 2016),但其优势是不需要额外的门。除了剩余连接之外,还可以使用从每一层到输出的可学习的跳过连接。在实验中,我们评估了剩余连接和层到输出连接的相对有效性。
3.4. Masked Convolution
网络中每一层每个输入位置的h特征被分成三个部分,每个部分对应一个RGB通道。当预测当前像素![]() 的R通道时,只能使用生成
的R通道时,只能使用生成![]() 的左上方像素作为上下文。在预测G通道时,除了前面生成的像素外,R通道的值还可以用作上下文。同样,对于B通道,可以使用R和G通道的值。为了将网络中的连接限制为这些依赖项,我们对输入状态卷积和PixelRNN中的其他纯卷积层应用了一个Mask。
的左上方像素作为上下文。在预测G通道时,除了前面生成的像素外,R通道的值还可以用作上下文。同样,对于B通道,可以使用R和G通道的值。为了将网络中的连接限制为这些依赖项,我们对输入状态卷积和PixelRNN中的其他纯卷积层应用了一个Mask。
我们使用两种类型的Mask,用Mask A和Mask B表示,如图2(右)所示。Mask A只应用于PixelRNN中的第一个卷积层,限制与相邻像素和当前像素中已经预测的颜色的连接。另一方面,将Mask B应用于所有后续的input-to-state convolutional transition,并通过允许颜色到自身的连接,来放松Mask A的限制。通过在每次更新之后对输入到状态的卷积中的相应权重进行归零,可以很容易地实现Mask。Mask也用于变分自编码器。
3.5. PixelCNN
Row and Diagonal LSTM层在它们的接受域内有一个潜在的无限依赖范围。这伴随着计算成本,因为每个状态都需要按顺序计算。一个简单的解决方法是使接受域变大,但不是无限制的。我们可以使用标准的卷积层来捕获一个有界的接收域,并同时计算所有像素位置的特征。PixelCNN使用多个卷积层来保持空间分辨率;不使用池层。在卷积中采用Mask,以避免看到未来的上下文;Mask以前也被用于非卷积模型,如MADE (Germain et al., 2015)。注意,PixelCNN相对于PixelRNN的并行化优势只存在于训练或测试图像评估期间。这两种网络的图像生成过程都是连续的,因为每个采样的像素都需要作为输入返回到网络中
3.6. Multi-Scale PixelRNN
Multi-Scale PixelRNN由unconditional PixelRNN和一个或多个conditional PixelRNNs组成。unconditional PixelRNN首先以标准方式生成一个较小的s x s图像,该图像是从原始图像中进行子采样的。然后,条件网络将s x s图像作为额外的输入,生成一个更大的n x n图像,如图2(中间)所示。条件网络类似于标准的PixelRNN,但是它的每一层都带有小s x s图像的上采样版本。上采样和偏置过程定义如下。在上采样过程中,利用卷积网络的反卷积层构造一个尺寸为c x n x n的放大feature map,其中c是上采样网络输出map中feature的个数。然后,在偏置过程中,对于条件PixelRNN中的每一层,简单地将c x n x n条件映射为4h x n x n映射,并将其添加到相应层的输入状态映射中;这是使用一个1x1反掩码卷积来实现的。然后像往常一样生成更大的n x n图像。
4. Specifications of Models
在这一部分中,我们给出了实验中使用的像素网络的规格。我们有四种网络:基于Row LSTM的PixelRNN、基于Diagonal BiLSTM的PixelRNN、全卷积的PixelRNN和Multi-Scale PixelRNN。
表1指定了单尺度网络中的每一层。第一层是一个使用a型掩码的7 x 7卷积。这两种类型的LSTM网络然后使用可变数量的递归层。该层中的输入到状态卷积使用B类型的掩码,而状态到状态卷积没有掩码。PixelCNN使用了大小为33的卷积和类型为b的掩码。然后,顶部的feature map通过由一个经过校正的线性单元(ReLU)和一个1x1个卷积组成的几层。
在CIFAR-10和ImageNet实验中,这些层有1024个特征图;对于MNIST实验,这些层有32个特征图。剩余连接和层到输出连接跨所有三个网络的层使用。实验中使用的网络具有以下超参数。对于MNIST,我们使用一个对角线BiLSTM,它有7层,值h = 16(第3.3节和图5右侧)。对于CIFAR-10,行和对角BiLSTMs有12层,h = 128个单元。PixelCNN有15层,h = 128。对于32 x 32 ImageNet,我们采用12层行LSTM, h = 384个单元;对于64 x 64 ImageNet,我们使用4层行LSTM, h = 512个单元;后一种模型不使用剩余连接。
5. Experiments
在本节中,我们将描述我们的实验和结果。我们从描述评估和比较结果的方式开始。在5.2节中,我们给出了关于训练的详细信息。然后给出了体系结构组件的相对有效性的结果,以及MNIST、CIFAR-10和ImageNet数据集上的最佳结果。
5.1. Evaluation
所有的模型都是基于离散分布的对数似然损失函数进行训练和评估的。虽然自然图像数据通常使用密度函数进行连续分布建模,但是我们可以用以下方法将我们的结果与之前的技术进行比较。
在文献中,目前最好的做法是在像素值中加入重值噪声,在使用密度函数时对数据进行去量化(Uria et al., 2013)。当加入均匀噪声(取值区间为[0,1])时,连续和离散模型的对数似然性是直接可比的(Theis et al., 2015)。在本例中,我们可以将离散分布的值作为分段均匀连续函数使用,对于每个区间![]() 。当前位置当前位置这个对应的分布将具有与原始离散分布相同的对数似然(对添加噪声的数据)。对于MNIST,我们报道了nats中的负对数可能性,因为这在文献中很常见。对于CIFAR-10和ImageNet,我们报告了每维位的负对数概率。总离散对数似然通过图像的维数进行归一化(例如,CIFAR-10的32 x 32 x 3 = 3072)。这些数字可以解释为基于该模型的压缩方案压缩每个RGB颜色值(van den Oord & Schrauwen, 2014b; Theis et al., 2015);在实践中,由于算术编码也有一个小的开销。
。当前位置当前位置这个对应的分布将具有与原始离散分布相同的对数似然(对添加噪声的数据)。对于MNIST,我们报道了nats中的负对数可能性,因为这在文献中很常见。对于CIFAR-10和ImageNet,我们报告了每维位的负对数概率。总离散对数似然通过图像的维数进行归一化(例如,CIFAR-10的32 x 32 x 3 = 3072)。这些数字可以解释为基于该模型的压缩方案压缩每个RGB颜色值(van den Oord & Schrauwen, 2014b; Theis et al., 2015);在实践中,由于算术编码也有一个小的开销。
5.2. Training Details
我们的模型使用Torch工具箱在gpu上进行培训。从所尝试的不同参数更新规则来看,RMSProp具有最佳的收敛性能,适用于所有的实验。每个数据集的学习速率表都被手动设置为允许快速收敛的最大值。批处理大小也因不同的数据集而异。对于较小的数据集,如MNIST和CIFAR-10,我们使用16幅图像的较小批处理大小,因为这似乎使模型规范化。对于ImageNet,我们使用GPU内存允许的最大批处理大小;这对应于32 x 32 ImageNet的64张图片/批处理,以及64 x 64 ImageNet的32张图片/批处理。除了在网络输入处缩放和居中图像外,我们不使用任何其他预处理或增强。对于多项式损失函数,我们使用原始像素颜色值作为类别。对于所有的PixelRNN模型,我们学习了网络的初始递归状态。
5.3. Discrete Softmax Distribution
除了直观和易于实现外,我们发现在离散像素值上使用softmax而不是在连续像素值上使用混合密度方法可以得到更好的结果。对于具有软最大输出分布的行LSTM模型,我们在CIFAR- 10验证集上得到3.06位/dim。我们得到3.22位/dim。
在图6中,我们展示了来自模型的几个softmax激活。虽然我们没有嵌入256个颜色类别的意义或关系的先验信息,例如像素值51和52是相邻的,但是模型预测的分布是有意义的,可以是多模态的、倾斜的、峰值的或长尾的。还要注意,值0和255的概率通常要高得多,因为它们出现的频率更高。离散分布的另一个优点是,我们不用担心分布质量位于区间[0,255]之外的部分,而这通常发生在连续分布中。
5.4. Residual Connections
网络的另一个核心组件是剩余连接。在表2中,我们展示了在12层CIFAR-10 Row LSTM模型中具有剩余连接、具有标准跳过连接或同时具有这两种连接的结果。我们看到,使用剩余连接与使用跳过连接一样有效;同时使用这两种方法也是有效的,并保留了优势。
当同时使用剩余连接和跳过连接时,我们在表3中看到,Row LSTM的性能随着深度的增加而提高。这适用于我们尝试的12个LSTM层。
5.5. MNIST
尽管我们工作的目标是大规模的自然图像模型,我们也尝试过我们的模型的二进制版本(Salakhutdinov &Murray,2008) MNIST (LeCunet al ., 1998),因为它是一个很好的完整性检查和以前有很多艺术在这个数据集比较。在表4中,我们报告了对角BiLSTM模型的性能和以前发表的结果。据我们所知,这是迄今为止MNIST上报道的最好的结果。
5.6. CIFAR-10
接下来,我们在CIFAR-10数据集上测试我们的模型(Krizhevsky, 2009)。表5列出了我们的模型和以前发布的方法的结果。我们所有的结果都是在没有增加数据的情况下得到的。对于所提出的网络,对角BiLSTM的性能最好,其次是行LSTM和PixelCNN。这与各自接受域的大小一致:对角线BiLSTM具有全局视图,行LSTM具有部分遮挡视图,PixelCNN在上下文中看到的像素最少。这表明有效地捕捉一个大的接受域是很重要的。图7(左)Diagonal BiLSTM.显示了生成的CIFAR-10示例。
5.7. ImageNet
虽然据我们所知,ILSVRC ImageNet数据集(Russakovsky et al., 2015)上还没有发表过我们可以用来比较模型的结果,但我们给出了ImageNet log-likelihood表现(不增加数据)。
在ImageNet上,当前的pixelrns并没有出现过拟合,因为我们看到它们的验证性能随着大小和深度的增加而提高。模型大小的主要限制是当前的计算时间和GPU内存。注意,ImageNet模型通常比CIFAR-10图像的可压缩性更差。ImageNet图像种类较多,CIFAR-10图像最多可能使用与我们在ImageNet图像中使用的算法不同的算法来调整大小。ImageNet图像的模糊程度较低,这意味着相邻像素之间的相关性较低,因此较难预测。由于下采样方法会影响压缩性能,因此我们使用了常用的下采样图像。
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第1张图片](http://img.e-com-net.com/image/info8/4cc3e0e0fbb44460a1e70448c3ef4b2f.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第2张图片](http://img.e-com-net.com/image/info8/86f9831635034362b3eec385d0770b38.jpg)
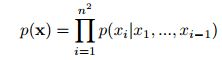
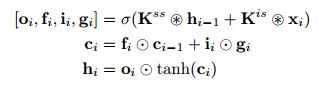
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第3张图片](http://img.e-com-net.com/image/info8/b9eb248f40224522b68d5402c1b8f913.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第4张图片](http://img.e-com-net.com/image/info8/082ad941da294117b811dc8dd6365712.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第5张图片](http://img.e-com-net.com/image/info8/d6d5ab2269804fe68db3468fbf3a5d66.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第6张图片](http://img.e-com-net.com/image/info8/d5f070a6c76948bd859f906925b4fb04.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第7张图片](http://img.e-com-net.com/image/info8/24fbcaa436d64b49b63bad6e1eb48178.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第8张图片](http://img.e-com-net.com/image/info8/bed879ec5f7b406ba73c96ab60b24224.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第9张图片](http://img.e-com-net.com/image/info8/0a64e171edd34c25902e62c7e23c1e18.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第10张图片](http://img.e-com-net.com/image/info8/dac88e273e8546b0af212a36ae1567ea.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第11张图片](http://img.e-com-net.com/image/info8/ca32eae506af424b82558010825c33aa.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第12张图片](http://img.e-com-net.com/image/info8/9540229509e747f2bbc5b71e1143136c.jpg)
![(21)[ICML16] PixelRNN:Pixel Recurrent Neural Networks_第13张图片](http://img.e-com-net.com/image/info8/2263286507744bae84b522a7d0d3fb30.jpg)