通俗理解:Logistic Regression【学习笔记】
1、提出问题
比如
- 问题1,在信用评分模型中,如何判断某个人的违约概率
- 问题2,在图像识别领域,如何判断一张图片的动物是不是猫
- 问题3,给定某个人的体重、年龄,判断其体脂高低
- 问题4,在物品详情页,线上一个用户点击进来了,如何给出推荐列表,即找到ta最可能点击哪些商品。CTR
- 问题5,通过一个人的年龄、性别、血压、胆固醇水平、体重等,想知道这个人患心脏病的概率
- …等等
以问题3为例:已收集到样本(X,Y)
- X = ( x 1 , x 2 , x 3 , . . . , x n ) X=(x_1, x_2, x_3, ..., x_n) X=(x1,x2,x3,...,xn)
- Y = ( y 1 , y 2 , y 3 , . . . , y n ) , y i ∈ ( 0 或 1 ) Y=(y_1, y_2, y_3, ..., y_n), y_i\in(0或1) Y=(y1,y2,y3,...,yn),yi∈(0或1)
- w = ( w 1 , w 2 , w 3 , . . . , w n ) w=(w_1, w_2, w_3, ..., w_n) w=(w1,w2,w3,...,wn) 是 X X X的权重值
现在给一个人的体重(weight)、年龄(age),如何判断其体脂高低?
我们需要得到一个预测函数 s ( X T w ) s(X^Tw) s(XTw)(线性模型),在输入样本 X X X过程中,不断尝试不同的 w w w(学习过程),输出样本:
- Y = 1 Y=1 Y=1的概率为 p p p( Y = 0 Y=0 Y=0的概率为 1 − p 1-p 1−p),从而判断这个人体脂高低:
- s ≥ 0.5 s≥0.5 s≥0.5,体脂高,正样本,标记为1;
- s < 0.5 s<0.5 s<0.5,体脂低,负样本,标记为0;
得出: p = s ( X T w ) p=s(X^Tw) p=s(XTw)
一个事情(如体脂【高】或者【低】)发生的概率 p p p和影响这个事情发生的因素(如身高、年龄)之间存在一种关系。
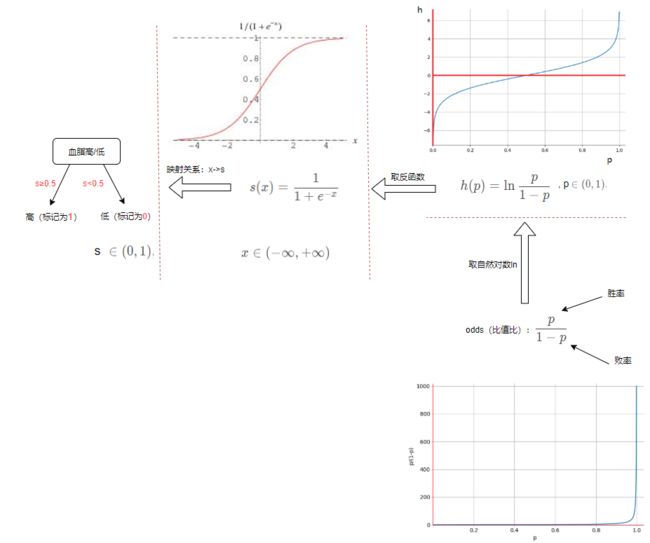
2、现在的问题是: s ( X T w ) s(X^Tw) s(XTw)是什么?
换个思路,得到 s ( x ) s(x) s(x)的反函数 h ( x ) h(x) h(x),于是:
X T w = h ( p ) X^Tw=h(p) XTw=h(p)
如果知道了 h ( p ) h(p) h(p),那么, s ( X T w ) s(X^Tw) s(XTw)就很容易得到了。
3、现在的问题变为: h ( p ) h(p) h(p)怎么得到?
我们需要的 h ( p ) h(p) h(p)函数是这样的:
- h ( p ) h(p) h(p)是一个 p ∈ ( 0 , 1 ) p\in(0,1) p∈(0,1)之间变化一个函数。
- h ( p ) h(p) h(p)是一个在 p = 0 p=0 p=0或 p = 1 p=1 p=1附近, p p p的微小变化,对应 h ( p ) h(p) h(p)(即 X T w X^Tw XTw)的较大变化;同时 h ( p ) h(p) h(p)要足够简单。
于是,从 h ( p ) h(p) h(p)变化入手,想到了求导,寻找到一个符合要求的函数:
d ( h ( p ) ) d ( p ) = 1 1 − p + 1 p \frac{d(h(p))}{d(p)}=\frac{1}{1-p}+\frac{1}{p} d(p)d(h(p))=1−p1+p1
这个式子 1 1 − p + 1 p \frac{1}{1-p}+\frac{1}{p} 1−p1+p1就在 p = 0 p=0 p=0或 p = 1 p=1 p=1附近,数值是接近于 ∞ \infty ∞,也就是变化很大。那么对上述式子积分(即知道了函数的导函数,反求原函数)得到:
h ( p ) = ln p 1 − p h(p)=\ln\frac{p}{1-p} h(p)=ln1−pp
附 ( u v ) ′ = u ′ v − u v ′ v 2 (\frac{u}{v})^′=\frac{u^′v-uv^′}{v^2} (vu)′=v2u′v−uv′
根据上述的 h ( p ) = X T w h(p)=X^Tw h(p)=XTw,因此:
ln p 1 − p = X T w ⇒ p 1 − p = e X T w ⇒ p = e X T w 1 + e X T w = 1 1 + e − X T w \ln\frac{p}{1-p}=X^Tw \Rightarrow \frac{p}{1-p}=e^{X^Tw} \Rightarrow p=\frac{e^{X^Tw}}{1+e^{X^Tw}} = \frac{1}{1+e^{-X^Tw}} ln1−pp=XTw⇒1−pp=eXTw⇒p=1+eXTweXTw=1+e−XTw1
即结论是: p = 1 1 + e − X T w = s ( X T w ) p = \frac{1}{1+e^{-X^Tw}}=s(X^Tw) p=1+e−XTw1=s(XTw)
得到最终的Logistic函数为:
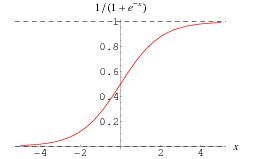
s ( x ) = 1 1 + e − x ∈ ( 0 , 1 ) , x ∈ ( − ∞ , + ∞ ) s(x)=\frac{1}{1+e^{-x}} \in (0, 1), x \in (-\infty, +\infty) s(x)=1+e−x1∈(0,1),x∈(−∞,+∞)
总结:
上述函数 s ( x ) = 1 1 + e − x ∈ ( 0 , 1 ) , x ∈ ( − ∞ , + ∞ ) s(x)=\frac{1}{1+e^{-x}} \in (0, 1), x \in (-\infty, +\infty) s(x)=1+e−x1∈(0,1),x∈(−∞,+∞)称之为Logistic函数(或 Sigmoid函数),用于二元分类(任务)中,输出事件概率:即 当输出满足某一个概率条件时,我们就将其划分为正或负样本。
是机器学习中一个常用的函数,与之类似的有softmax、softplus等函数。最早可追溯到1844年,一个比利时的数学家用于模仿一些情况人口增长的S形曲线,除了应用人类学,还可应用于数学、动物学、机器学习领域。
使用Logistic函数 很容易将预测值 分为两类:
- 将预测概率小于0.5的分为负样本,标记为0;
- 将预测概率大于0.5的分为正样本,标记为1。
而Sigmoid函数对输入超出一定范围就会不敏感(从图像可知 x x x趋向于正负无穷大时)。
所以,Logistic Regression最常见的应用场景是:预测概率。
从【国内】翻译角度理解(不推荐):Logistic Regression
Logistic Regression(简写 LR),逻辑回归 或逻辑斯蒂回归。
从单词(词根)的角度
logistic adj.逻辑的;n.数理(符号)逻辑,逻辑斯蒂
↓
logic 译为 n.逻辑 adj.逻辑的,这词是个舶来品,是音译
在本文的【逻辑回归算法】中的【逻辑】不是中文常说的【逻辑思维】这种逻辑。或译成:逻辑斯蒂回归。以避免误导性。
logistic指的是 logistic函数
-------------------------------------------------------------
regression = re + gress + sion
↓ ↓ ↓
回/向后/相反 | to go/walk行走,来自拉丁语 | 名词后缀
=>翻译:向后走
根据上述推导过程,最准确的翻译应该是:对数几率回归