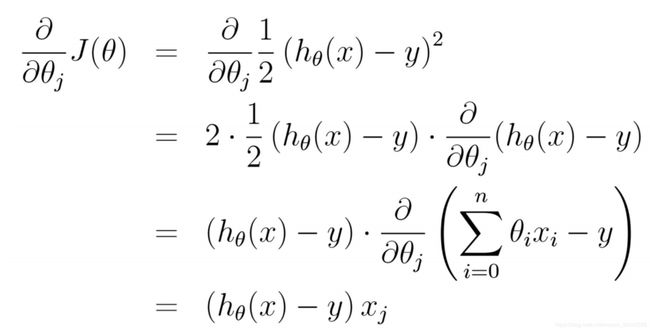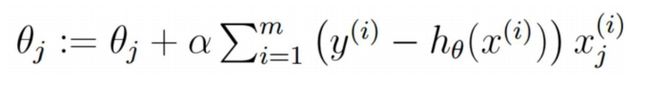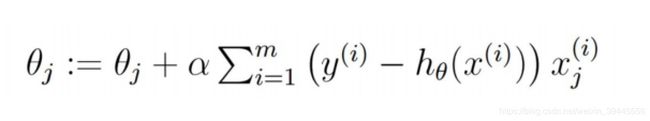梯度下降与随机梯度下降概念及推导过程
接前一章:常用算法一 多元线性回归详解2(求解过程)
同这一章的梯度下降部分加起来,才是我们要讲的如何求解多元线性回归.如果写在一章中,内容过长,担心有的同学会看不完,所以拆分成两章.[坏笑]
上一章中有提到利用解析解求解多元线性回归,虽然看起来很方便,但是在解析解求解的过程中会涉及到矩阵求逆的步骤.随着维度的增多,矩阵求逆的代价会越来越大(时间/空间),而且有些矩阵没有逆矩阵,这个时候就需要用近似矩阵,影响精度.所以本章我们一起来学习求解多元线性回归最常用的,也是后边可能会讲的深度学习最常用的求解办法:梯度下降与随机梯度下降.
其实随机梯度下降才是咱们最常用的求解办法,但是不知道梯度下降,理解随机梯度下降就有些直接盖二楼的感觉了(我的意思是空中楼阁).那什么是梯度下降呢?
从字面意思上,我们就可以get到他最重要的点--梯度.所以首先我们来看梯度的概念.(事先声明,好多概念纯粹为了方便理解)
什么是梯度:
1-先看官方解释:
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
2-通俗理解:
我们对一个多元函数求偏导,会得到多个偏导函数.这些导函数组成的向量,就是梯度.
这里需要开拓一下你聪明的头脑.一元函数的梯度是什么?思考一下.它的梯度可以理解为就是它的导数.
我们求解一元函数的时候有一种办法是对函数求导得到导函数,令导函数为零得到这个函数的解析解.那我们可不可以理解为求解一元函数时利用让一元函数的梯度变为0的时候,梯度所在的位置就是函数的最优解呢? (稍稍有点偷天换日,但是在一元函数中梯度和导数并无区别,这块一定要理解)
梯度中元素(导函数)的个数的个数同未知数的个数是对应,每一个未知数都可以像求解一元一次函数一样,通过它所对应的梯度求得最优解.其实求解多元函数和一元函数的道理是一样的,只不过函数是一元的时候,梯度中只有一个导函数,函数时多元的时候,梯度中有多个导函数.
当我们把梯度中的所有偏导函数都变为0的时候,就可以找到每个未知数的对应解?(事实证明是这样的)
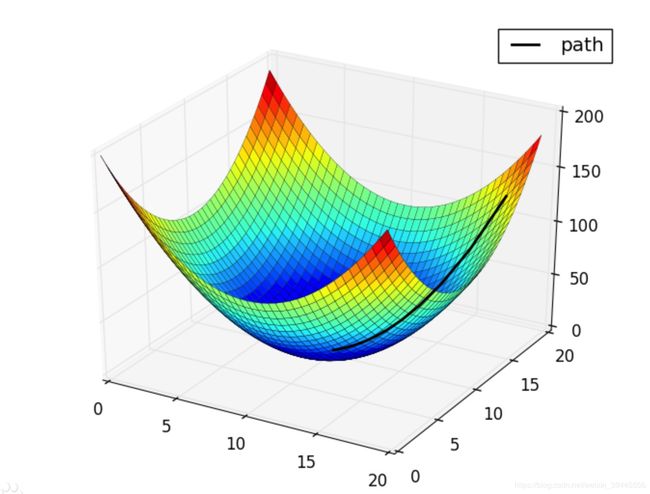
附上一张梯度的图
假设这个曲面是一个多元函数,我们可以把这个曲面看成是由无数条曲线组成,每条曲线代表了多元函数的一个维度,当所有维度都下降到梯度为0的点,是不是这个点就是多元函数的解的那个点呢?
什么是梯度下降:
1-还是按照惯例,先看官方解释.
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是解析解。
上一段来源于网络,对于咱们要理解的内容来看,上边一段等于没说.
2-通俗讲
梯度下降就是让梯度中所有偏导函数都下降到最低点的过程.(划重点:下降)
都下降到最低点了,那每个未知数(或者叫维度)的最优解就得到了,所以他是解决函数最优化问题的算法
这里需要注意一点,梯度是对所有未知数求偏导,所得偏导函数组成的向量.在多元线性回归中,谁才是未知数呢?我们使用梯度下降法的目的是求解多元线性回归中的最小二乘函数的,在最小二乘函数中,已拥有的条件是一些样本点和样本点的结果,就是矩阵X和每一条X样本的lable值y.X是矩阵,y是向量.
所以我们要知道,梯度下降中求偏导数的未知数不是x和y,而是x的参数W或者叫![]() (就是个名字,只不过常用这两个字母表示).
(就是个名字,只不过常用这两个字母表示).
数据集中数据是固定的,结果是固定的,我们要找到的是数据中样本与结果的对应规律.所以求得![]() 才是我们的目的.我们梯度下降,下降的也是
才是我们的目的.我们梯度下降,下降的也是![]() 而不是X.
而不是X.
怎样理解下降:
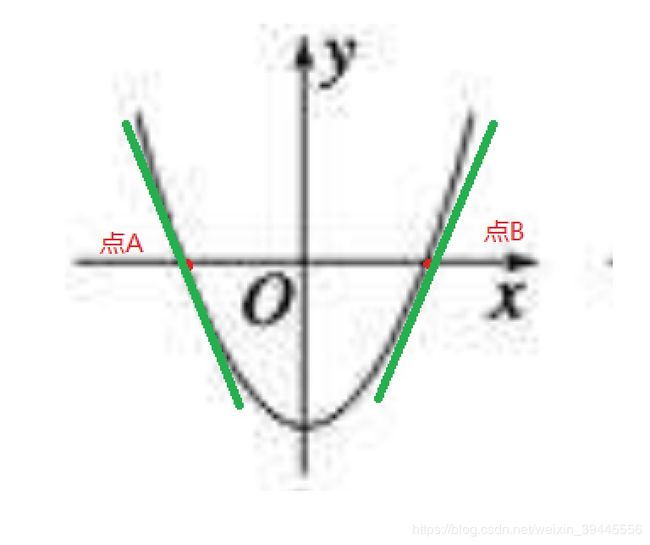
梯度下降中的下降,意思是让函数的未知数随着梯度的方向运动.什么是梯度的方向呢?把这一点带入到梯度函数中,结果为正,那我们就把这一点的值变小一些,同时就是让梯度变小些;当这一点带入梯度函数中的结果为负的时候,就给这一点的值增大一些.
如上图,点A的导函数(此时把导函数看作梯度)为负,就让点A沿着函数轨迹往右移动一点,点B的导数为正,就让点B往左移动一点,这个移动的过程中,点A和店B的高度都在慢慢下降,所以这个过程叫做梯度下降.
在这个下降的过程中.因为我们并不知道哪一个点才是最低点,也没有办法来预测下降多少次才能到最低点.这里梯度下降给出的办法是:先随便蒙一个点出来,然后根据这个点每次下降以丢丢.什么时候下降得到的值(点带入偏导函数得到的)和上一次的值基本基本一样也就是相差特别特别小的时候,我们认为就到了最低点.
当然这里有两个问题:
1-这个值并不是完全准确:
我们并不需要一个完完全全准确的值来当做函数的解,因为多元线性回归构的理念中就讲了,我们是用一条回归线来预测未来结果,本身我们预测出的这个结果就存在一个误差,所以梯度下降的结果是否完全准确并不特别重要.
2-如果函数图像是一个波浪形,我们只能找到其中一个浪谷的最低点,这个点可能不是所有浪谷最低点中的最小值.
我们初始点的位置是随机蒙出来的造成了这种情况,多次随机可以有效解决解决这个问题.
如果我们多次有规律的随机都没有采集到的最低点,可能是因为这个最低点造成的原因是出现了某个离群值.(这句话不用理解,你就记得其实是不是最小值也并不是特别重要就行了.)
函数在点![]() 或
或![]() 的移动过程如何用公式来表达呢?公式如下:
的移动过程如何用公式来表达呢?公式如下:
![]() (公式一)
(公式一)
公式中,![]() 为当前时刻的
为当前时刻的![]() 值,
值,![]() 为下一时刻的
为下一时刻的![]() 值.g为梯度.
值.g为梯度.![]() 是一个正数,我们先不看他.
是一个正数,我们先不看他.
此时我们随机一个点,将这个点叫做k+1点,如果它的梯度为正,那么按照公式一,我们会将这个给它的梯度减去一个正数,得到一个k+1点梯度更小的梯度的点k;如果k+1的梯度像图一的点B一样梯度为负数,此时我们减去一个负数,就等于给他加了一个正数,得到的k点的梯度要比原来k+1点的梯度大.
所以,按照公式一,无论k+1点的梯度是正还是负,我们都可以让他沿着函数图像向比原来更低的方向运动.
![]() 是什么:是学习率
是什么:是学习率
我们把公式一中的![]() 叫做学习率.
叫做学习率.
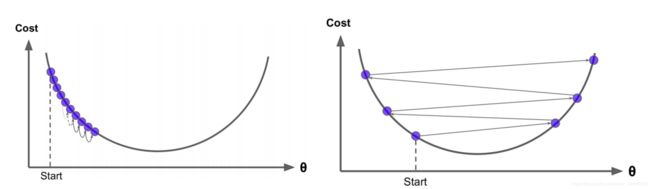
让点沿着梯度方向下降慢慢求得最优解的过程我们叫做学习,学习率就是用来限制他每次学习别太过"用功"的,因为机器学习也存在书呆子[奸笑].请看下图:
图二中,左图是我们所期望的,一个点按照梯度方向下降,慢慢逼近最低点,右图中展示的就是那个书呆子.模型每次下降都是减去梯度的值,当这个梯度值过大的时候,点下降的step就过大了,一次性迈过了最低点,导致函数无法找到最优解.
![]() 就是来限制这种情况的.我们让梯度乘以一个很小的数,虽然增加了它到达最低点的step数,但是可以让图二这种情况发生概率降低.
就是来限制这种情况的.我们让梯度乘以一个很小的数,虽然增加了它到达最低点的step数,但是可以让图二这种情况发生概率降低.
到现在,我们知道了梯度下降法到底是什么,也知道了每一步是如何下降的,按照这个方法一次一次迭代下降就可以得到函数的最优解.但是还有很重要的一点:如何求梯度.
重复一下:梯度就是对一个多元函数的未知数求偏导,得到的偏导函数构成的向量就叫梯度.那我们要求解的多元函数是哪个?
是最小二乘函数:
![]() (公式二)
(公式二)
求导过程如下:
公式三种,![]() 是
是![]() ,y所有样本点的lable值向量y.得到的公式(
,y所有样本点的lable值向量y.得到的公式(![]() )
)![]() 中,
中,![]() 是一个维度的所有数据,(
是一个维度的所有数据,(![]() )
)![]() 本身是对这个维度的所有数据求梯度的和.所以我们得到梯度下降中的梯度g:
本身是对这个维度的所有数据求梯度的和.所以我们得到梯度下降中的梯度g:
g=![]() 1/m x (
1/m x (![]() )
)![]() . m为样本点的个数.
. m为样本点的个数.
公式的另一种表达形式:
到这里,梯度下降就讲解完毕了.梯度下降又叫做批量梯度下降,简称BGD.
(休息两分钟)
下面我们来看随机梯度下降(SGD):
批量梯度下降是,求出一个维度中所有的数据,取个平均来当做每一次梯度下降的step.这样做虽然准确,但是每次要计算一个维度的所有数据的梯度,花费资源较大.所以才有了随机梯度下降的思想:每次只随机取一个维度中的一条数据求梯度,来当做这个维度梯度下降的step.公式如下:
可以看出,随机梯度下降和梯度下降公式的区别就是,里边的x由矩阵x变成了x的分量![]()
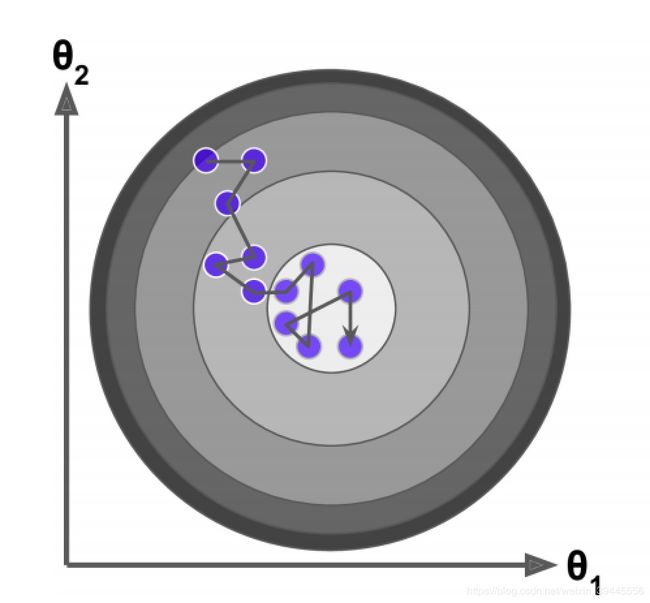
为了更好的让大家理解梯度下降和随机梯度下降的区别,看下图:
途中,蓝色点为两个![]() 的取值,圆形越靠近里边表示误差越小.
的取值,圆形越靠近里边表示误差越小.
BGD总是综合所有数据的梯度,取到的下降至一直很平滑,SGD随机抽取一条数据作为参数,步子很不稳定.但是最终都可以到达函数的最优解位置.虽然看起来SGD比BGD的误差要大一些,但是SGD随着迭代次数的增加,误差会越来越小.
最后,SGD因为每次只随机抽取一条数据来做梯度下降,计算代价比SGD小的不是一点半点.所有后边无论机器学习还是深度学习,对SGD的应用是非常非常广泛的.
在SGD和BGD中间,还有一个集合了两种下降法的有点的办法:mini-bach-GD,你猜一猜他是啥?对了,是随机抽取小批量数据来做下降,但是用的并不多.
利用梯度下降法求解梯度的过程:
一般情况下分为三步:
1-随机一个初始值,在多元线性回归中,我们随机一组w,带入到损失函数中,得到一个初始点.
2-让这个点按照负梯度的方向运动,就是我们前边讲的 ![]() ,梯度的计算如上文所述.
,梯度的计算如上文所述.
3-迭代第二步,当迭代此处达到某一个数,或者上一步和这一步的结果误差小于某个数,就认为是最优解了,停止迭代.迭代次数和最小误差值都是可以设置的.
通过第三步,我们就可以得到一个我们想要的最优解.
最后补充一点,梯度下降的公式![]() (公式一)看起来好像开玩笑一样就定下来了,没有任何依据,其实不是这样的,它背后的理论依据是泰勒展开式.这里不再过多赘述了.文章就到这里,请大家帮忙勘误.
(公式一)看起来好像开玩笑一样就定下来了,没有任何依据,其实不是这样的,它背后的理论依据是泰勒展开式.这里不再过多赘述了.文章就到这里,请大家帮忙勘误.
(写文章很耗神,如果对您有帮助,欢迎点赞和评论)
下一篇:零基础理解 逻辑回归(logistics regression)