三、回归——logistic回归二分类的python实现

一、训练算法：使用梯度上升找到最佳参数

1.使用Logistic回归梯度上升优化算法

       每次更新回归系数都要遍历整个数据集，该算法在处理100左右各样本时还可以，但是如果有数十亿样本或者成千上万的特征，那么该算法就太过于复杂了。

import os
from numpy import *

os.chdir("E:\python learning\Machine Learning in Action\machinelearninginaction\Ch05")  #设置路径
#打开文件并逐行读取,每行的前两个值是特征值X1,X2，第3列是数据对应的标签
def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()  #去掉头尾的空格，并以空白字符为分隔符进行分割
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])   #并将dataMat矩阵的第一列设置为1
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat   #输出特征矩阵和标签矩阵
dataArr,labelMat = loadDataSet()

#定义sigmoid函数
def sigmoid(inX):
    return 1.0/(1+exp(-inX))

#定义梯度上升算法函数，其中dataMatIn参数为2维numpy数组，每列代表不同的特征，每行代表一个训练样本，labelMat为标签分类
def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)             #convert to NumPy matrix
    labelMat = mat(classLabels).transpose() #convert to NumPy matrix
    m,n = shape(dataMatrix)                 #获取矩阵的行和列
  
    alpha = 0.001
    maxCycles = 500
    weights = ones((n,1))   #n为矩阵dataMatIn的列数，也就是变量的个数
    for k in range(maxCycles):              #heavy on matrix operations
        h = sigmoid(dataMatrix*weights)     #matrix mult,计算z值
        error = (labelMat - h)              #vector subtraction，计算预测值域实际值的偏差
        weights = weights + alpha * dataMatrix.transpose()* error #matrix mult  #梯度下降算法，找出最佳的参数
    return weights

#计算参数
weights = gradAscent(dataArr,labelMat)

2.分析数据：画出决策边界

#画出决策边界：画出数据集和logistic回归最佳拟合直线的函数
def plotBestFit(wei):
    import matplotlib.pyplot as plt
    dataMat,labelMat=loadDataSet()  #导入数据
    dataArr = array(dataMat)        #dataMat转换为数组
    n = shape(dataArr)[0]           
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    
    #将数据按类别分类
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(-3.0, 3.0, 0.1)
    y = (-wei[0]-wei[1]*x)/wei[2]
    ax.plot(x, y)
    plt.xlabel('X1'); plt.ylabel('X2');
    plt.show()

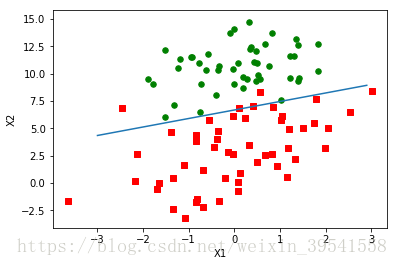
plotBestFit(weights.getA())

最后的分类结果如下，从图中看只错分了两到四个点，但是这个例子所需要的计算量非常大，下面会对这一算法进行改进。

二、训练算法：随机梯度上升

      由于梯度上升算法只适合100左右各样本的数据集的计算，在样本量大时该方法就会变得太过于复杂。一种改进的方法就是一次只使用一个样本点来更新回归系数，该方法就称为随机梯度上升算法。由于随机梯度上升算法可以在新样本点到来时对分类器进行增量式更新，因此随机梯度上升是一个在线学习的算法。与“在线学习”相对应的是一次性处理所有样本，称为“批处理”。

随机梯度上升算法可以写成以下的伪代码：

所有回归系数初始化为1

对数据集中每个样本

                计算该样本的梯度

                使用alpha * gradient更新回归系数值

返回回归系数值

1.随机梯度上升算法

#随机梯度上升算法没有矩阵的转换过程，所有变量的数据类型都是Numpy数组。前面的梯度上升算法有矩阵的转换过程
#随机梯度上升算法的变量h和误差error都是数值，梯度上升算法的为向量
def stocGradAscent0(dataMatrix, classLabels):
    m,n = shape(dataMatrix)  #计算数组的形状
    alpha = 0.01
    weights = ones(n)   #initialize to all ones
    for i in range(m):  #m为样本量
        h = sigmoid(sum(dataMatrix[i]*weights))   #每次值计算一个样本点
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights

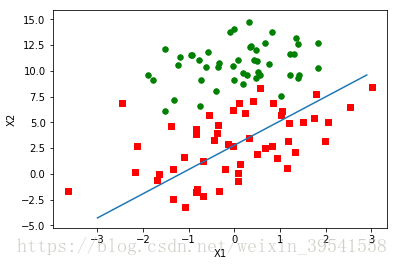
dataArr,labelMat = loadDataSet()
weights1 = stocGradAscent0(array(dataArr),labelMat)
plotBestFit(weights1)

2.改进的随机梯度上升算法

（1）改进一：alpha在每次迭代中都会调整，在一定程度上可以缓解数据波动或高频波动，虽然alpha会随每次迭代次数不断减小，但是永远不会减小到0，必须这样做的原因是为了保证在多次迭代之后新数据仍然具有一定的影响，如果要处理的问题是动态变化的，name可以适当加上常数项，来确保新的值可以获得更大的回归系数

（2）改进二：这里通过随机选取样本来更新回归系数，这种方法将减少周期性的波动。

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = shape(dataMatrix)
    weights = ones(n)   #initialize to all ones
    for j in range(numIter):   #增加迭代次数
        dataIndex = list(range(m))     #这里应该修改
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.0001    #alpha在每次迭代中都会减小，但是不会为0，这样保证在多次迭代之后新数据仍然对参数有影响
            randIndex = int(random.uniform(0,len(dataIndex))) #随机抽取样本来更新参数
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

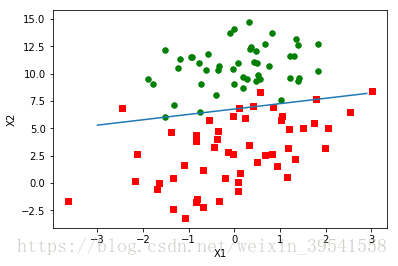
dataArr,labelMat = loadDataSet()
weights2 = stocGradAscent1(array(dataArr),labelMat)
plotBestFit(weights2)

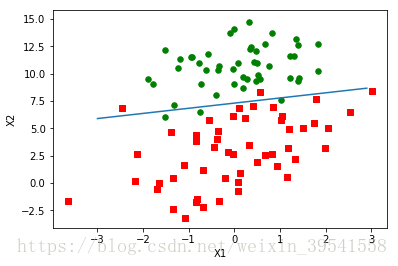
#默认的迭代次数是150次，可以更改为500
weights3 = stocGradAscent1(array(dataArr),labelMat,500)
plotBestFit(weights3)

默认的迭代次数是150次，这里可以更改为500次来看效果

三、示例：从疝气病症预测病马的死亡率

1.使用logistic回归估计马疝病的死亡率(从疝气病症预测病马的死亡率).步骤：

（1）收集数据：给定数据文件
（2）准备数据：用python解析文本文件并填充缺失值
（3）分析数据：可视化并观察数据
（4）训练算法：使用优化算法，找到最佳的系统
（5）测试算法：为了量化回归的效果，需要观察错误率。根据错误率决定是否回退到训练阶段，通过改变迭代的次数和步长等参数来得到更好的回归系数

（6）使用算法：实现一个简单的命令行程序来收集马的症状并输出预测结果。

2.代码实现：

#classifyVector的第一个参数为回归系数,weight为特征向量，这里将输入这两个参数来计算sigmoid值，如果只大于0.5，则返回1，否则返回0.
def classifyVector(inX, weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5: return 1.0    #如果不想得到分类，则直接返回prob概率
    else: return 0.0

#打开数据集并对数据集进行处理
def colicTest():
    frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt')
    trainingSet = []; trainingLabels = []
    
    #获取训练集的数据，并将其存放在list中
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr =[]            #用于存放每一行的数据
        for i in range(21):    #这里的range(21)是为了循环每一列的值，总共有22列
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))    
    trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000)   #用改进的随机梯度算法计算回归系数
   
    #计算测试集的错误率
    errorCount = 0; numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
            #如果预测值和实际值不相同，则令错误个数加1
        if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]):
            errorCount += 1
    errorRate = (float(errorCount)/numTestVec)    #最后计算总的错误率
    print ("the error rate of this test is: %f" % errorRate)
    return errorRate

#调用coicTest函数10次并求平均值
def multiTest():
    numTests = 10; errorSum=0.0
    for k in range(numTests):
        errorSum += colicTest()
    print ("after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests)))

multiTest()

返回值如下：
multiTest()
__main__:2: RuntimeWarning: overflow encountered in exp
the error rate of this test is: 0.358209
the error rate of this test is: 0.313433
the error rate of this test is: 0.417910
the error rate of this test is: 0.358209
the error rate of this test is: 0.373134
the error rate of this test is: 0.328358
the error rate of this test is: 0.328358
the error rate of this test is: 0.298507
the error rate of this test is: 0.343284
the error rate of this test is: 0.328358

after 10 iterations the average error rate is: 0.344776

源数据下载：https://download.csdn.net/download/weixin_39541558/10467472

本文为作者原创，如要转载，请注明出处，谢谢！！