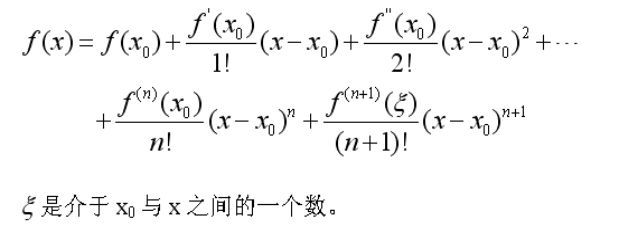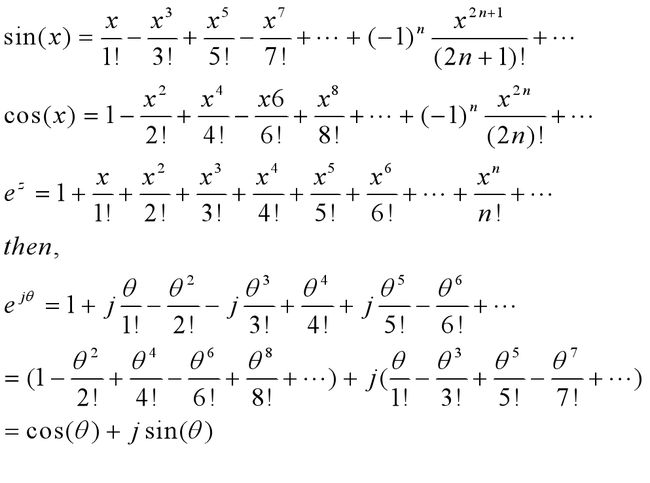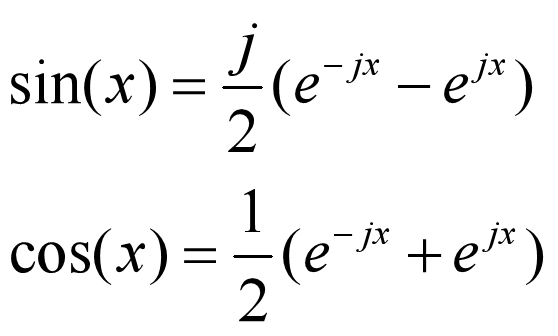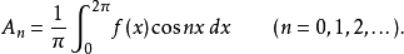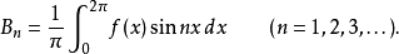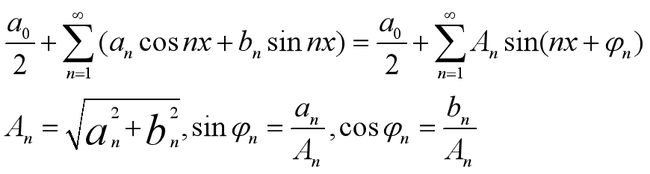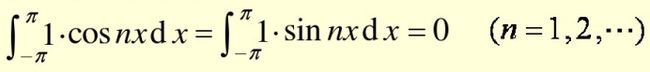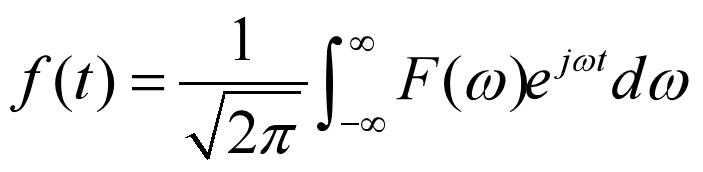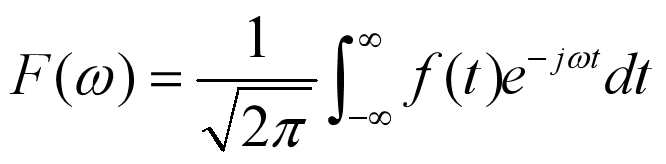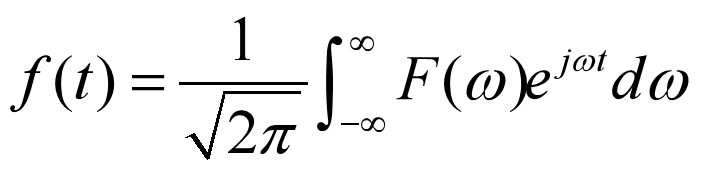《数字图像处理》第5讲——傅里叶变换
虽然写这个博客主要目的是为了给我自己做一个思路记忆录,但是如果你恰好点了进来,那么先对你说一声欢迎。我并不是什么大触,只是一个菜菜的学生,如果您发现了什么错误或者您对于某些地方有更好的意见,非常欢迎您的斧正!
目录
楔子
①傅里叶变换的作用
②知识储备
1、泰勒级数
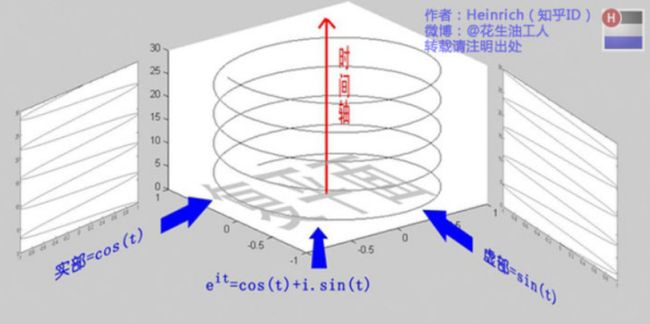
2、欧拉公式(真正的宇宙第一公式)
3、三角级数
4、三角函数系的正交性
③傅里叶变换对
④傅立叶变换的相关概念
⑤一维傅立叶逆变换
⑥傅立叶谱的平移
⑦傅立叶变换频谱
⑧二维Fourier变换的应用
1、Fourier变换在图像滤波中的应用
2、Fourier变换在图像压缩中的应用
3、Fourier变换在卷积中的应用
楔子
之前就已经总结过一次,但是我觉得真的写的晦涩难懂,都是公式,让我感觉哪怕以后自己再看这篇文章,连自己都不会有勇气去读完它。于是只好破釜沉舟,重新学习傅里叶!(其实我已经学过这个了,现在学习这个数字图像处理,竟然又遇到了傅里叶,不得不感慨,它真的无所不在!大学里总是伴随着泰勒、拉格朗日、柯西、傅里叶,但是不得不承认,傅里叶变换真的很牛!)我不是知识的讲述者,我只是一个大佬们对这些知识的理解的搬运工。
强烈推荐两篇文章:
傅里叶分析之掐死教程(完整版)
https://zhuanlan.zhihu.com/p/19763358
欧拉公式——真正的宇宙第一公式
http://k.sina.com.cn/article_6385529085_17c9b70fd001006gjp.html?from=science
以下就是正文部分了。
①傅里叶变换的作用
首先你搜索“傅里叶变换”,你将得到一个公式:
你会想,它的意义是什么呢?我要这个公式有何用!
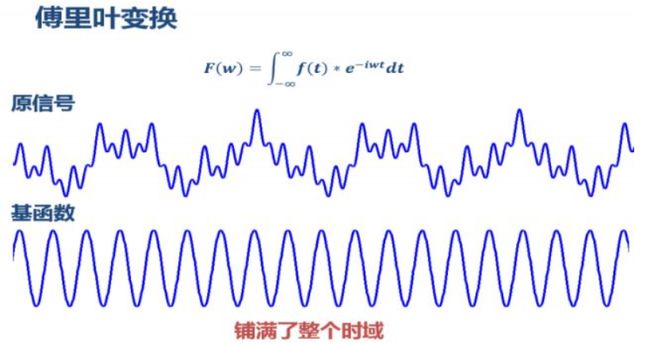
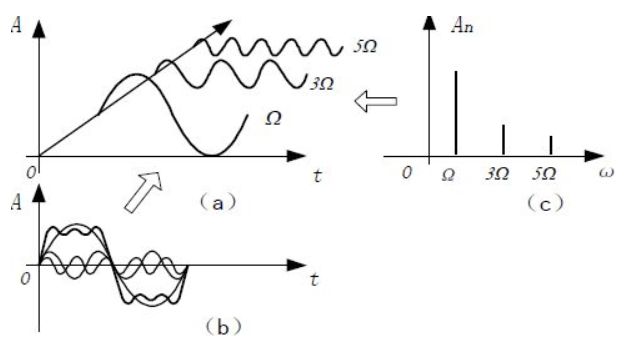
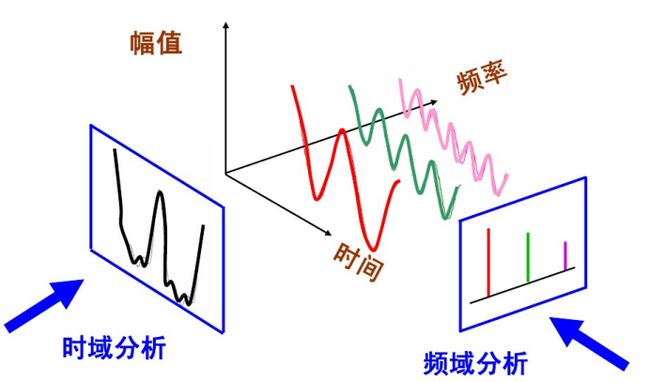
我们不难发现,傅里叶变换总是伴随着“信号”,看一下下图中这个原信号,是不是晦涩难懂,而傅里叶变换的作用,就是将这样一个复杂的波形拆分成简单的正弦波或余弦波的叠加。(任何连续周期信号可以由一组适当的正弦曲线组合而成)
就像这样:从b->a->c的巨大演变,只需要一个傅里叶!
②知识储备
1、泰勒级数
这又是一个麻烦的东西,泰勒级数是干什么用的呢?
就是用多项式函数去逼近光滑函数。
(https://www.zhihu.com/question/21149770)
这是我在网上看到的一个解释,我觉得是最贴切的解释了!
还有一幅图可以感受一下,请点击这里。(打不开就用下面的链接)
https://www.matongxue.com/madocs/7.html
接下来看一下它的系统性定义,以及一些常见的泰勒级数,就不多讲了。
泰勒级数:如果函数f(x)在它含点x0的某一区间(a,b)内具有的任何导数都存在,因此对任何正整数n,有下面的n阶泰勒公式成立
2、欧拉公式(真正的宇宙第一公式)
作用:将正弦波统一成了简单的指数形式
![]()
它的图像意义:
3、三角级数
在数学中,三角级数是任何具有下述形式的级数:
当![]() 和
和![]() 具有以下形式时,该级数称为傅立叶级数:
具有以下形式时,该级数称为傅立叶级数:
其中![]() 是可积函数。
是可积函数。
傅里叶级数是一种三角级数,傅里叶级数也常称为三角级数。但并不是所有三角级数都是傅立叶级数。
4、三角函数系的正交性
组成三角级数的函数系:1,cosx,sinx,cos2x,sin2x,...,cosnx,sinnx,...
1)其中任意两个不同的函数之积在[-π,π]上的积分等于0
2)两个相同的函数的乘积在[-π,π]上的积分不等于0
将三角函数展开成傅里叶级数
③傅里叶变换对
④傅立叶变换的相关概念
⑤一维傅立叶逆变换
⑥傅立叶谱的平移
![]()
⑦傅立叶变换频谱
⑧二维Fourier变换的应用
1、Fourier变换在图像滤波中的应用
首先,我们来看Fourier变换后的图像,中间部分为低频部分,越靠外边频率越高。因此,我们可以在Fourier变换图中,选择所需要的高频或是低频滤波。
2、Fourier变换在图像压缩中的应用
变换系数刚好表现的是各个频率点上的幅值。在小波变换没有提出时,用来进行压缩编码。考虑到高频反映细节、低频反映景物概貌的特性。往往认为可将高频系数置为0,骗过人眼。
3、Fourier变换在卷积中的应用
从前面的图像处理算法中知道,如果抽象来看,其实都可以认为是图像信息经过了滤波器的滤波(如:平滑滤波、锐化滤波等 )。 如果滤波器的结构比较复杂时,直接进行时域中的卷积运算是不可思议的。
参考文章(感谢大佬!):
傅里叶分析之掐死教程(完整版)
https://zhuanlan.zhihu.com/p/19763358
欧拉公式——真正的宇宙第一公式
http://k.sina.com.cn/article_6385529085_17c9b70fd001006gjp.html?from=science