SLAM十四讲第五次作业-深蓝学院
void computeAngle(const cv::Mat &image, vector<cv::KeyPoint> &keypoints) {
int half_patch_size = 8;
for(auto &kp : keypoints){
// START YOUR CODE HERE (~7 lines)
//judge if keypoint is on edge
int x=cvRound(kp.pt.x);
int y=cvRound(kp.pt.y);
if( x-half_patch_size<0||x+half_patch_size>image.cols||
y-half_patch_size<0||y+half_patch_size>image.rows)
continue; //结束当前循环,进入到下一次循环
double m01=0,m10=0; //定义变量的时候,要初始化,不然这里第一张图片所有kp.angle=0
for(int i=-half_patch_size;i<half_patch_size;i++){ //-8
for(int j=-half_patch_size;j<half_patch_size;j++){
m01 += j*image.at<uchar>(y+j,x+i); //真实坐标(j,i)+(y,x)
m10 += i*image.at<uchar>(y+j,x+i); //获得单个像素值image.at(y,x)
}
}
kp.angle = atan(m01/m10)*180/pi;
cout<<"m10 = "<<m01<<" "<<"m01 = "<<m10<<" "<<"kp.angle = "<<kp.angle<<endl;
// END YOUR CODE HERE
}
return;
}
- 为什么要有这一步?
为了让描述子面对图像旋转时,仍然有效!
先让p、q按照keypoint的角度进行旋转,使得图像旋转后,p与q的位置相对于keypoint不发生旋转,然后再进行像素大小比较,再进行keypoints匹配。
void computeORBDesc(const cv::Mat &image, vector<cv::KeyPoint> &keypoints, vector<DescType> &desc) {
for (auto &kp: keypoints) {
DescType d(256, false);
for (int i = 0; i < 256; i++) {
// START YOUR CODE HERE (~7 lines)
auto cos_ = float(cos(kp.angle*pi/180)); //将角度转换成弧度再进行cos、sin的计算
auto sin_ = float(sin(kp.angle*pi/180));
//注意pattern中的数如何取
cv::Point2f p_r(cos_*ORB_pattern[4*i]-sin_*ORB_pattern[4*i+1],
sin_*ORB_pattern[4*i]+cos_*ORB_pattern[4*i+1]);
cv::Point2f q_r(cos_*ORB_pattern[4*i+2]-sin_*ORB_pattern[4*i+3],
sin_*ORB_pattern[4*i+2]+cos_*ORB_pattern[4*i+3]);
cv::Point2f p(kp.pt+p_r); //获取p'与q'的真实坐标,才能获得其像素值
cv::Point2f q(kp.pt+q_r);
// if kp goes outside, set d.clear()
if(p.x<0||p.y<0||p.x>image.cols||p.y>image.rows||
q.x<0||q.y<0||q.x>image.cols||q.y>image.rows){
d.clear();
break;
}
//像素值比较
d[i]=image.at<uchar>(p)>image.at<uchar>(q)?0:1; // 这里的“>”不可以替换成“-”,因为用“-”,结果是负数和正数都为真,是0的时候为假。
// END YOUR CODE HERE
}
desc.push_back(d);
}
int bad = 0;
for (auto &d: desc) {
if (d.empty()) bad++;
}
cout << "bad/total: " << bad << "/" << desc.size() << endl;
return;
}
void bfMatch(const vector<DescType> &desc1, const vector<DescType> &desc2, vector<cv::DMatch> &matches) {
int d_max = 50;
// START YOUR CODE HERE (~12 lines)
// find matches between desc1 and desc2.
for(int i=0;i<desc1.size();i++){
if(desc1[i].empty())
continue;
int d_min=256 ,index=-1; //必须定义在这里,每次循环重新初始化
for(int j=0;j<desc2.size();j++){ //这个for循环,取出最小的d_min
if(desc2[j].empty())
continue;
int d=0; //必须定义在这里,每次循环重新初始化
for(int k=0;k<256;k++){
d += desc1[i][k]^desc2[j][k]; //异或:不同为1;
}
if(d<d_min){
d_min=d;
index=j;
}
}
if(d_min<=d_max){
cv::DMatch match(i,index,d_min);
matches.push_back(match);
}
}
// END YOUR CODE HERE
for (auto &m: matches) {
cout <<"queryIdx = "<< m.queryIdx << ", " << "trainIdx = "<<m.trainIdx << ", " << "distance = "<<m.distance << endl;
}
return;
}
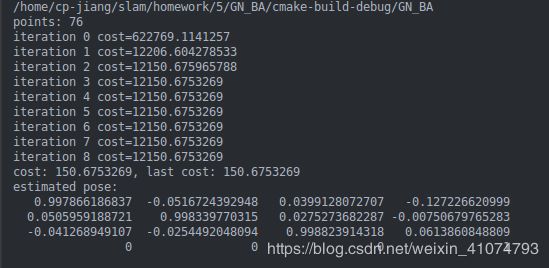
结果截图:


答:
1.因为ORB的描述子采用的是0和1表示。
2.取更大有很多误匹配,取更小匹配的点较少。
3.0.27秒,FLANN可以减少时间。

#include //
// Created by xiang on 12/21/17.
//
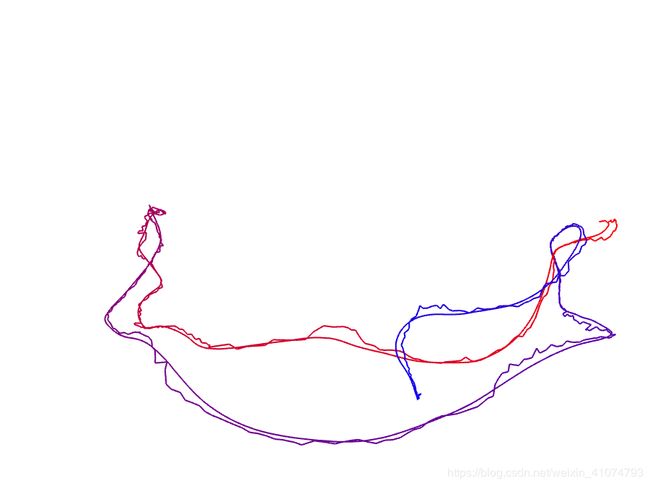
#include //用ICP实现轨迹对齐
//把两条轨迹的平移部分看作点集,然后求点集之间的 ICP,得到两组点之间的变换T_eg
#include