布隆过滤器 原理 应用场景推导及Go实现
Bloom Filter(布隆过滤器)
布隆过滤器是一种多哈希函数映射的快速查找算法,通常应用在一些需要快速判断某个元素是否属于集合,但并不严格要求100%正确的场合。
Bloom算法类似一个hash set,用来判断某个元素(key)是否在某个集合中。
和一般的hash set不同的是,这个算法无需存储key的值,对于每个key,只需要k个比特位,每个存储一个标志,用来判断key是否在集合中。
布隆过滤器可能会出现误判,但不会漏判。即,如果过滤器判断该元素不在集合中,则元素一定不在集合中,但如果过滤器判断该元素在集合中,有一定的概率判断错误(在合适的参数情况下,误判率可以降低到0.000级别甚至更低)。
因此,Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下,Bloom Filter相比于其他常见的算法极大节省了空间(相较于直接存储,可节省上千倍的空间)。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是存在误识别率和删除困难。
优点:
相比于其它的数据结构,布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数。另外, Hash 函数相互之间没有关系,方便由硬件并行实现。布隆过滤器不需要存储元素本身,在某些对保密要求非常严格的场合有优势。
布隆过滤器可以表示全集,其它任何数据结构都不能;
k 和 m 相同,使用同一组 Hash 函数的两个布隆过滤器的交并差运算可以使用位操作进行。
- 不需要存储key,节省空间
缺点:
但是布隆过滤器的缺点和优点一样明显。误算率(False Positive)是其中之一。随着存入的元素数量增加,误算率随之增加。但是如果元素数量太少,则使用散列表足矣。
另外,一般情况下不能从布隆过滤器中删除元素. 我们很容易想到把位列阵变成整数数组,每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。
- 算法判断key在集合中时,有一定的概率key其实不在集合中
- 无法删除
典型的应用场景:
某些存储系统的设计中,会存在空查询缺陷:当查询一个不存在的key时,需要访问慢设备,导致效率低下。
比如一个前端页面的缓存系统,可能这样设计:先查询某个页面在本地是否存在,如果存在就直接返回,如果不存在,就从后端获取。但是当频繁从缓存系统查询一个页面时,缓存系统将会频繁请求后端,把压力导入后端。
这是只要增加一个bloom算法的服务,后端插入一个key时,在这个服务中设置一次
需要查询后端时,先判断key在后端是否存在,这样就能避免后端的压力。
- 网页黑名单
- 垃圾邮件过滤
- 电话黑名单
- url去重
- Redis缓存穿透
- 比特币钱包查询
- 内容推荐等
算法步骤:
- 首先需要k个hash函数,每个函数可以把key散列成为1个整数
- 初始化时,需要一个长度为n比特的数组,每个比特位初始化为0
- 某个key加入集合时,用k个hash函数计算出k个散列值,并把数组中对应的比特位置为1
- 判断某个key是否在集合时,用k个hash函数计算出k个散列值,并查询数组中对应的比特位,如果所有的比特位都是1,认为在集合中。
首先需要用到 bitset? 和计算hash 的2个库。
import(
"github.com/willf/bitset" //bitset
"github.com/spaolacci/murmur3" //hash计算
"math"
)
哈希函数 - Murmur hash3
murmur hash是一种非加密型哈希函数,适用于一般的哈希检索操作。对于规律性较强的key,murmurhash的随机分布特征表现更良好。相比于md5,murmur hash在万次测试中,性能高4-5倍。
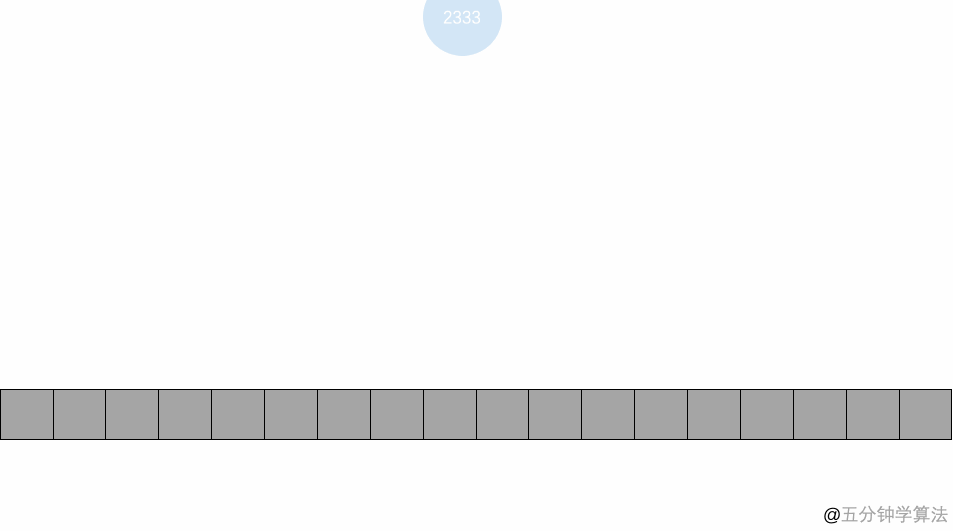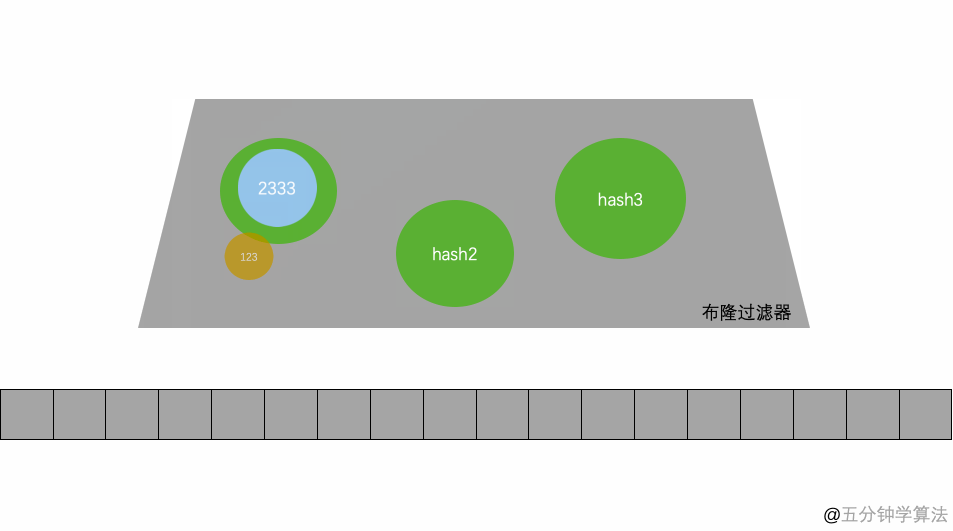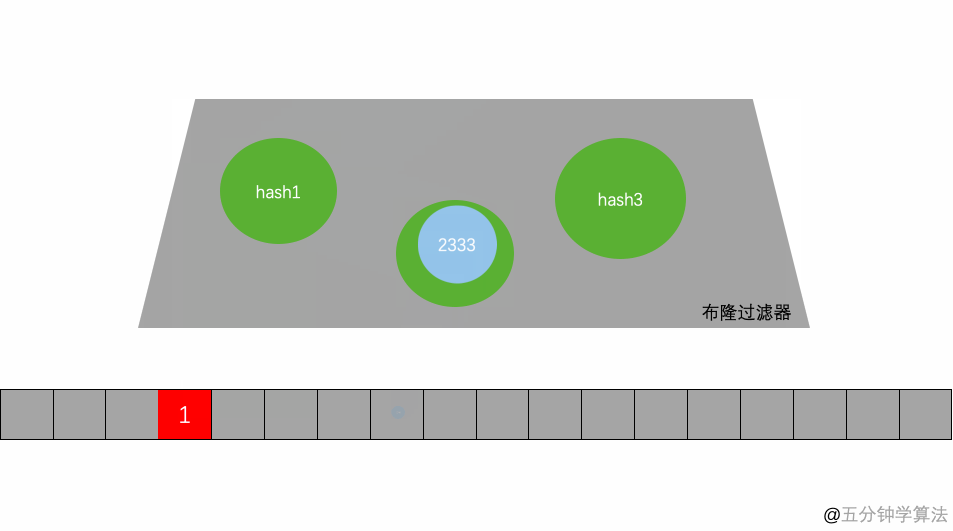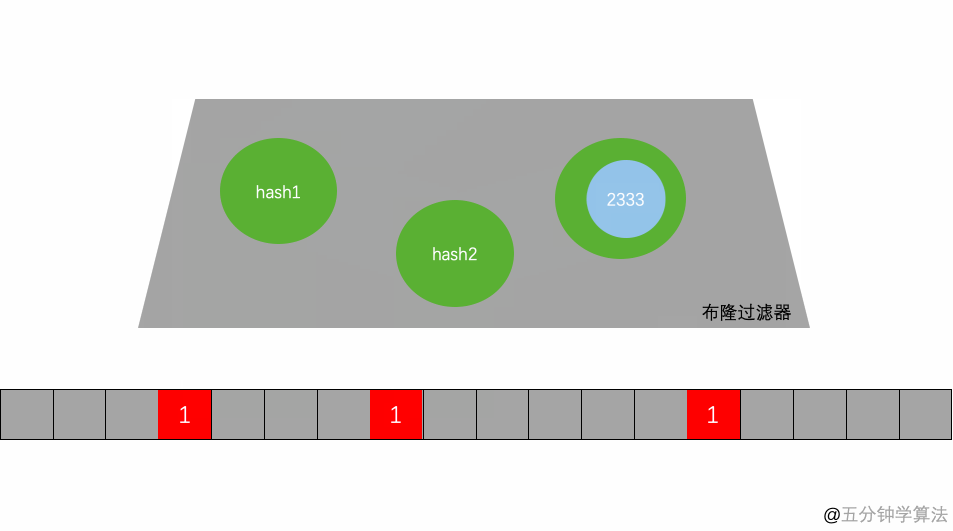
下面定义布隆 过滤器的基础结构。
type BloomFilter struct {
m uint //布隆过滤器key的个数
k uint //hash函数的个数
b *bitset.BitSet //所有value
}
//比大小
func max(x,y uint)uint{
if x > y {
return x
}
return y
}
新建一个布隆 过滤器,mSet 就是 一个存储 10101101 的数组 而 要判断一个键,存在与否就是 找到散列在这个mSet上的值是否都设置为了1,但现实中的数据分布肯恩个会非常不均匀导致有些 位的重复率特别高 这样会影响,查询寻得准确率导致一些没有的键也能被查到,所以需要用到散列函数,将数字或者文本散列在一个列表各个bit上,同时由于文本不能存储在bitset中,所以hash函数还能帮助文本进行 去重。

func NewBloomFilter(m uint,k uint) *BloomFilter{
return &BloomFilter{
m: max(1,m), //最小1个
k: max(1,k),//同理
b: bitset.New(m),//bitmap
}
}
根据数据量新建布隆过滤器,每多加一个数 容量就会添加64.
func From(data []uint,k uint)*BloomFilter{
m := uint(len(data)*64)
return &BloomFilter{
m: m,
k: k,
b: bitset.From(data),
}
}
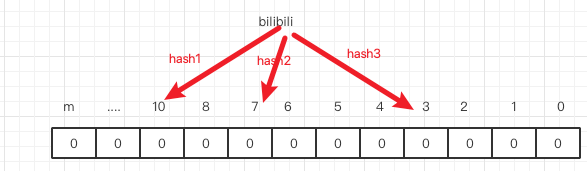
如上图 存放一个字符串 先将字符串hash 成 k = 3 个 hash整数 存在了 HashSet中。这所以用多个Hash 确认一个Key主要是可以减少误判(不存在的Key 判断为了存在)的概率。
给定 数据 返回四个 hash的整数
func bashHashes(data []byte) [4]uint64{
X := []byte{1}
haser := murmur3.New128() //128的hash 2^128
haser.Write(data) //2个整数 1578830625359084202 6865968778589710305
v1,v2 := haser.Sum128()
haser.Write(X)
v3,v4 := haser.Sum128() // 2个整数
return [4]uint64{v1,v2,v3,v4} //返回四个整数
}
下面就是 输入上面生成的四个随机hash整数,然后通过运算可以生成K个整数,用于散列在bitset上。
func (f *BloomFilter) location(h [4]uint64,i uint) uint{
//对计算处的位置 求余 找到 布隆过滤器中的位置
return uint(location(h,i) % uint64(f.m))
}
//
func location(h [4]uint64,i uint) uint64{
ii := uint64(i)
//hash 这个公式 是将 4 个 uint64 和 i 进行计算 传入不同的i 可以算出不同的Hash i是 0 ~ k 个 。
return h[ii %2] + ii*h[2+(((ii+(ii % 2))%4)/2)]
}
重复出现的概率
布隆过滤器出现误判的几率和 他的大小是有关的,假设 布隆过滤器 有 m个元素,n个元素,每个元素散列 k个信息指纹的哈希函数。 每一个 bit位 被置为 1的概率p(a)是一样的: P ( a ) = 1 m P(a) = \frac{1}{m} P(a)=m1,所以每一位上不为0的概率为 1 − p ( a ) = 1 − 1 m 1 - p(a) = 1 - \frac{1}{m} 1−p(a)=1−m1 那么对于散列在HashSet上确定一个key的 K个散列值,不为0的概率为 ( 1 − 1 m ) k (1 - \frac{1}{m})^k (1−m1)k,假设第二个键插入到hashSet中,不重复的概率为 ( 1 − 1 m ) k ⋅ ( 1 − 1 m ) k = ( 1 − 1 m ) 2 k (1 - \frac{1}{m})^k · (1 - \frac{1}{m})^k = (1 - \frac{1}{m})^{2k} (1−m1)k⋅(1−m1)k=(1−m1)2k 同理可得,
如果有N个不同的键通过K个散列Hash插入到大小为M的hashSet中某个位不重复的概率为: ( 1 − 1 m ) k n (1 - \frac{1}{m})^{kn} (1−m1)kn,
再取反,在插入了N的Key后某一位不重复的概率为: 1 − ( 1 − 1 m ) k n 1-(1- \frac{1}{m})^{kn} 1−(1−m1)kn,
假设来了一个新的Key 要让他误判成Key已经存在,相当于 要让k位hash散列Bit都在已有的表中出现,而某一位重复出现的概率就是上面的公式,那么K位重复的概率就是: ( 1 − ( 1 − 1 m ) k n ) k ≈ ( 1 − e k n m ) k (1-(1- \frac{1}{m})^{kn})^{k} ≈ (1 - e^{\frac{kn}{m}})^k (1−(1−m1)kn)k≈(1−emkn)k,
推理过程为,当n比较大时,
引入一个我们很熟悉的公式: ( 1 − 1 m ) − m ≈ e (1 - \frac{1}{m})^{-m} ≈ e (1−m1)−m≈e 大学都应该有学过。
所以可以变形为:
( 1 − e − k n m ) k (1 - e ^{\frac{-kn}{m}})^k (1−em−kn)k。
接下来 假设错误率 p ( e ) = ( 1 − e − k n m ) k p(e) = (1 - e ^{\frac{-kn}{m}})^k p(e)=(1−em−kn)k
对公示两边取自然对数:
l n p = k l n ( 1 − e − k n m ) lnp = kln(1 - e ^{\frac{-kn}{m}}) lnp=kln(1−em−kn)
然后再进行求导:
= ∂ k l n ( 1 − e − k n m ) ∂ k = \frac{\partial{kln}(1 - e ^{\frac{-kn}{m}})}{\partial{k}} =∂k∂kln(1−em−kn) = l n ( 1 − e − k n m ) + k n m e − k n m 1 − e − k n m ln(1 - e^{\frac{-kn}{m}}) + k\frac{\frac{n}{m}e^{\frac{-kn}{m}}}{1 - e^{\frac{-kn}{m}}} ln(1−em−kn)+k1−em−knmnem−kn
∂ l n p ∂ k = l n ( 1 − x ) − x 1 − x \frac{\partial{lnp}}{\partial{k}} = ln(1 - x) - \frac{x}{1-x} ∂k∂lnp=ln(1−x)−1−xx
设 x = e − k n m x = e ^{\frac{-kn}{m}} x=em−kn $则 k = − m n l n x k = \frac{-m}{n}lnx k=n−mlnx
得 : ∂ l n p ∂ k = l n ( 1 − x ) − x 1 − x ∗ l n x \frac{\partial{lnp}}{\partial{k}} = ln(1 -x) - \frac{x} {1-x} * lnx ∂k∂lnp=ln(1−x)−1−xx∗lnx
对 ∂ l n p ∂ k \frac{\partial{lnp}}{\partial{k}} ∂k∂lnp 取极限0, x = 1 2 x = \frac{1}{2} x=21 最后解得 k 为: m n l n 2 \frac{m}{n}ln2 nmln2
当hash函数个数 k = ln2 * m / n 时错误率最小。
以下是 不同m/n 情况下 不同多个k 出现误判的几率:

布隆过滤器论文
对于给定 错误率 p,如何选择最优的位数的数组大小呢?
m = − n l n p ( l n 2 ) 2 m = -\frac{nlnp}{(ln2)^2} m=−(ln2)2nlnp
用来计算最合适的k个hash k = m n l n 2 k=\frac{m}{n}ln2 k=nmln2
假设 有 10 亿数据 错误率 0.01% 那要多少空间呢?
让我们来算一算 下面是python代码:
import math
n = 1000000000
p = 0.0001
m = -(n *math.log(p,math.e)/(math.log(2,math.e ) ** 2))
k = m/n * math.log(2,math.e )
m = m / 8 / 1024 /1024 / 1024
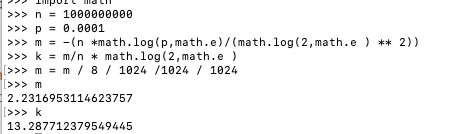
计算结果为 M为 2 .2 个G 左右 K 为 13 。这种情况下 10亿个数据也就会 误判1万个左右而且只用了 2个G 还是可以接受的。
下面用Go实现这两个公式,用来估计假阳性(不存在但查出来是存在)的概率和 用k个Hash 来存储一个key k的取值最合适的值。
func EStamatewithParameters(n uint,p float64) (m uint,k uint){
m = uint(math.Ceil( -1 * float64(n) * math.Log(p)) / math.Pow(math.Log(2),2))
k = uint(math.Ceil(math.Log(2) * float64(m)/float64(n)))
return m,k
}
//得到 多少蛇值多少个hash
func (f *BloomFilter)K()uint{
return f.k //hash
}
//包含的key大小
func (f *BloomFilter)Cap()uint{
return f.m//布隆过滤器存放的数据量
}
func (f *BloomFilter)Add(data []byte)*BloomFilter{
h := bashHashes(data)//计算哈希
for i:= uint(0);i<f.k;i++{
f.b.Set(f.location(h,i)) //设置数据
}
return f
}
//新建一个布隆过滤器,预估数据规模
func NewwithEstimates(n uint,p float64) *BloomFilter{
m,k := EStamatewithParameters(n,p)
return NewBloomFilter(m,k)
}
下面的代码 通过循环K次,通过f.location这个Hash计算函数计算出 f.k 个位置,设置到 bitset中。
func (f *BloomFilter)Add(data []byte)*BloomFilter{
//生成hash
h := bashHashes(data)
//循环k 次生成hash
for i:= uint(0);i<f.k;i++{
//把hash函数映射到对应的位置
f.b.Set(f.location(h,i))
}
return f
}
合并 就是 把 2 个 bitSet 合在一起,其实也就是执行或操作。
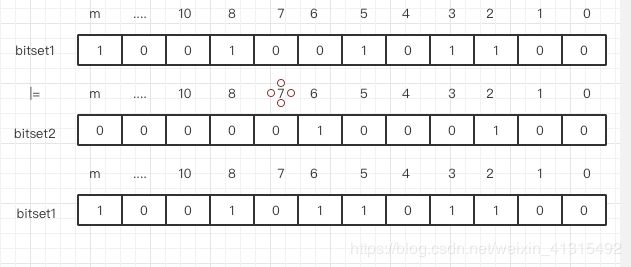
func (f *BloomFilter) Merge(g *BloomFilter)error{
if f.m != g.m{
return fmt.Errorf("大小不一样!")
}
if f.k != g.k{
return fmt.Errorf("Key不一样!")
}
f.b.InPlaceUnion(g.b) //归并 bitset
return nil
}
完整版:
type BloomFilter struct {
m uint //容量
k uint //hash函数个数
b *bitset.BitSet
}
func max(x,y uint)uint{
if x > y {
return x
}
return y
}
//新建一个布隆 过滤器
func NewBloomFilter(m uint,k uint) *BloomFilter{
return &BloomFilter{
m: max(1,m),
k: max(1,k),
b: bitset.New(m),
}
}
//根据数据量新建布隆过滤器
func From(data []uint64,k uint)*BloomFilter{
m := uint(len(data)*64)
return &BloomFilter{
m: m,
k: k,
b: bitset.From(data),
}
}
//对字符串进行hash
func bashHashes(data []byte) [4]uint64{
X := []byte{1}
haser := murmur3.New128() //128的hash 2^128
haser.Write(data)
v1,v2 := haser.Sum128()
haser.Write(X)
v3,v4 := haser.Sum128()
return [4]uint64{v1,v2,v3,v4}
}
func location(h [4]uint64,i uint) uint64{
ii := uint64(i)
return h[ii %2] + ii*h[2+(((ii+(ii % 2))%4)/2)]
}
func (f *BloomFilter) location(h [4]uint64,i uint) uint{
return uint(location(h,i) % uint64(f.m))
}
func EStamatewithParameters(n uint,p float64) (m uint,k uint){
m = uint(math.Ceil( -1 * float64(n) * math.Log(p)) / math.Pow(math.Log(2),2))
k = uint(math.Ceil(math.Log(2) * float64(m)/float64(n)))
return m,k
}
//新建一个布隆过滤器,预估数据规模
func NewwithEstimates(n uint,p float64) *BloomFilter{
m,k := EStamatewithParameters(n,p)
return NewBloomFilter(m,k)
}
func (f *BloomFilter)K()uint{
return f.k //hash
}
func (f *BloomFilter)Cap()uint{
return f.m//数量
}
func (f *BloomFilter)Add(data []byte)*BloomFilter{
h := bashHashes(data)
for i:= uint(0);i<f.k;i++{
f.b.Set(f.location(h,i))
}
return f
}
func (f *BloomFilter) Merge(g *BloomFilter)error{
if f.m != g.m{
return fmt.Errorf("大小不一样!")
}
if f.k != g.k{
return fmt.Errorf("Key不一样!")
}
f.b.InPlaceUnion(g.b) //归并 bitset
return nil
}
//拷贝新建一个布隆过滤器
func (f *BloomFilter)Copy() *BloomFilter{
fc := NewBloomFilter(f.m,f.k)
fc.Merge(f)
return fc
}
func (f *BloomFilter)AddString(data string)*BloomFilter{
return f.Add([]byte(data))
}
func (f *BloomFilter)Test(data []byte) bool{
h := bashHashes(data)
for i:= uint(0);i < f.k;i++{
if !f.b.Test(f.location(h,i)){
return false
}
}
return true
}
func (f *BloomFilter)TestString(data []byte) bool{
return f.Test([]byte(data))
}
//测试整数 是否存在
func (f *BloomFilter)TestLocations(locs []uint64) bool{
for i := 0;i<len(locs);i++{
if !f.b.Test(uint(locs[i] % uint64(f.m))){
return false
}
}
return true
}
//测试是否存在,存在就更新
func (f *BloomFilter)TestAndAdd(data []byte) bool{
isin := true
h := bashHashes(data)
for i := uint(0);i<f.k;i++{
if !f.b.Test(f.location(h,i)){
isin = false
}
f.b.Set(1)
}
return isin
}
//布隆过滤器的
type BloomFilterJson struct{
M uint `json:"m"`
K uint `json:"k"`
B *bitset.BitSet `json:"b"`
}
//字节转对象
func (f *BloomFilter)MarshaJson() ([]byte,error){
return json.Marshal(BloomFilterJson{f.m,f.k,f.b})
}
//字节转对象
func (f *BloomFilter)UnMarshaJson(data []byte) (error){
var j BloomFilterJson
err := json.Unmarshal(data,&j)
if err != nil{
return err
}
f.m = j.M
f.k = j.K
f.b = j.B
return nil
}
func (f *BloomFilter)Writeto(stream io.Writer)(int64,error){
err := binary.Write(stream,binary.BigEndian,uint64(f.m))
if err != nil{
return 0,err
}
err = binary.Write(stream,binary.BigEndian,uint64(f.k))
if err != nil{
return 0,err
}
bumbytes ,err := f.b.WriteTo(stream)
return bumbytes + int64(2 * binary.Size(uint64(0))),err
}
func (f *BloomFilter)Readfrom(stream io.Reader)(int64,error){
var m,k uint64
err := binary.Read(stream,binary.BigEndian,&m)
if err != nil{
return 0,err
}
err = binary.Read(stream,binary.BigEndian,&k)
if err != nil{
return 0,err
}
b := &bitset.BitSet{}
f.m = uint(m)
f.k = uint(k)
f.b = b
numbyte,err := b.ReadFrom(stream)
return numbyte + int64(2 *binary.Size(uint64(0))),err
}
func (f *BloomFilter) GoDecode(data []byte) (error){
buf := bytes.NewBuffer(data)
_,err := f.Readfrom(buf)
return err
}
func (f *BloomFilter) GoEncode() ([]byte,error){
var buf bytes.Buffer
_,err := f.Writeto(&buf)
if err != nil{
return nil,err
}
return buf.Bytes(),nil
}
func locations(data []byte,k uint) []uint64{
locs := make([]uint64,k)
h := bashHashes(data)
for i:= uint(0);i<k;i++{
locs[i] = location(h,i)
}
return locs
}
//判断布隆过滤器是否相等
func (f *BloomFilter) Equal (g *BloomFilter) bool{
return f.m == g.m && f.k == g.k && f.b.Equal(g.b)
}
//测试是否存在,存在就更新
func (f *BloomFilter)TestAndAddString(data []byte) bool{
return f.TestAndAdd([]byte(data))
}
//清空布隆过滤器
func (f *BloomFilter)Clear() *BloomFilter{
f.b.ClearAll()
return f
}
//测试正确率
func (f*BloomFilter)EstimateFalsePositiveRate(n uint,rounds uint32)(fpRate float64){
f.Clear()
n1:=make([]byte,4)//开辟字节数组
for i:=uint32(0);i<uint32(n);i++{
binary.BigEndian.PutUint32(n1,i)
f.Add(n1)//循环n次生成字节加入 布隆过滤器
}
fp:=0
for i:=uint32(0);i<rounds;i++{ //这里生成 数据测试 是不是在布隆过滤器里
binary.BigEndian.PutUint32(n1,i+uint32(n)+1)
if f.Test(n1) {
fp++
}
}
fpRate=float64(fp)/float64(rounds)//正确率
f.Clear()
return
}
测试代码:
f:=NewwithEstimates(100000000,0.001) //计算 1亿个数据 错误率为 0.001的情况下 m 和 k的值 并创建布隆过滤器
n1:=[]byte("123123")
n2:=[]byte("sdfsdf")
n3:=[]byte("dsfsdf")
n4:=[]byte("caomaoboy7777")
n5:=[]byte("helloworld")
f.Add(n1)
f.Add(n2)
f.Add(n3)
//这里测试序列化
data,_ := f.MarshaJson()
var g BloomFilter
err := g.UnMarshaJson(data)
if err != nil{
fmt.Println("error!")
}
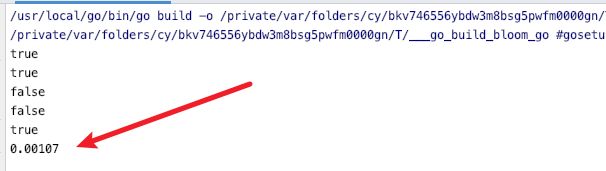
fmt.Println(f.Test(n1))
fmt.Println(f.Test(n3))
fmt.Println(f.Test(n4))
fmt.Println(f.Test(n5))
fmt.Println(f.Test(n3))
f.Clear()
fmt.Println(f.EstimateFalsePositiveRate(100000000)) //测试 插入100000000 如果正确的话 会输出 0.001左右的值
---------
参考:
吴军 – 《数学之美》
详解布隆过滤器(Bloomfilter)+scrapy分布式持久化去重 ----https://www.jianshu.com/p/e4773b69319d
详解布隆过滤器的原理、使用场景和注意事项 ----- https://www.jianshu.com/p/2104d11ee0a2
[算法系列之十]大数据量处理利器:布隆过滤器 -------https://yq.aliyun.com/articles/3607
Google算法工程师尹成带你深度学习数据结构与算法导论-----https://edu.51cto.com/course/20394.html?source=so