软件工程基础-个人项目-数独

个人项目–数独

1 项目地址

GitHub地址：https://github.com/Anne416wu/Sudoku

项目下载：git clone https://github.com/Anne416wu/Sudoku.git

• 需求：实现一个能够生成数独终局并且能求解数独问题的控制台程序
  • 生成数独终局
    1. sudoku -c N 生成N（ $1\le N\le 100000$ )个数独终局到文件sudoku.txt
    2. 对于sudoku -c abc 等异常输入能正确处理
    3. 数独矩阵左上角的第一个数为学号后两位对9的余数加1，对于2149，即$(4+9)\mathrm{m}\mathrm{o}\mathrm{d}9+1=5$
  • 生成数独问题
    1. sudoku -p N 生成sudoku.txt中N个数独终局对应的数独问题到文件ques.txt，挖空的数字用0代替
  • 求解数独
    1. sudoku -s absolute_pate_of_puzzle 从给出的文件路径（ques.txt）中读取数独问题，并将求解的结果输出到文件sudoku.txt
  • （附加题目）GUI界面
    • 生成任意数量的数独题目并将初始数独棋局依次显示。初始数独棋盘需要挖空，99棋盘上挖空不少于30个，不多于60个。每个33的小棋盘中挖空不少于2个
    • 用户可以在界面上通过点击或输入完成数独题目
    • 用户完成数独题目后可以得到反馈，知道自己的题目是否正确
• 作业要求
  1. 阅读PSP的相关资料
  2. 选择语言：C++
  3. 代码质量分析并消除所有警告：Clang-Tidy
  4. 完成项目的首个版本后。使用性能分析工具找出性能瓶颈并进行改进：
  5. 单元测试，查看测试分支覆盖率等指标，至少10个测试用例确保正确
  6. 使用GitHub托管源代码和测试用例
  7. 发布博客

2 PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	1	1
Estimate	估计项目总共需要时间	1	1
Development	开发	24	19
Analysis	需求分析	3	1
Design Spec	生成设计文档	1	1
Design Review	设计复审	1	1
Coding Standard	代码规范	1	2
Design	具体设计	3	2
Coding	编写代码	10	5
Code Review	代码复审	2	2
Testing	测试	2	5
Reporting	报告	5	7
Test Report	测试报告	2	3
Size Measurement	计算工作量	2	1
Postmortem & Process Improvement Plan	事后总结，提出改进计划	1	3
	Sum	30	27

3 思路描述

3.1 数独终局生成

数独终局规则：在一个9x9的数字表格中，每一行、每一列、每一个$3 \times 3 $的方块中，都包括数字1～9且不重复。

3.1.1. 暴力法

一种较为简单的数独终局生成方法。对于数独终局每一个格，通过随机数逐步产生数字，每次生成后检查一遍全局，复杂度为$O(n^2)$，效率较低。在需要生成

3.1.2. 全排列及行变换

一种较为普遍的数独终局生成方法。对于一个数独终局，在第一行固定的情况下，从第二行开始，每行在第一行的基础上，依次左移3、6、1、4、7、2、5、8格，就可以生成一个新的数独终局。假设数独终局的第一个数字固定为5，所以通过对第一行进行全排列的方式就可以产生$8!=40320$种终局。在每一个终局的基础上，通过任意交换2、3行，4、5、6行，7、8、9行，就可以产生新的终局。由此总共可以产生$40320\times 2!\times 3!\times 3!=2903040$种不同的终局，可以满足题目要求的$10^6$种

3.2 功能实现思路

3.2.1. 数独终局的生成

sudoku_generate(number)

使用3.1.2的方法：

1. 首先确定数独第一行，按照题目要求，以5开始，因此设置首行序列为5,1,2,3,4,6,7,8,9
2. 通过依次左移3、6、1、4、7、2、5、8格产生后八行，生成一个数独终局
3. 依次调换第一个数独终局2、3行，4、5、6行，7、8、9行的输出顺序，可生成$2!\times 3!\times 3!=72$个不同数独终局
4. 对第一行的序列使用next_permutation(first, last) 函数进行1～9进行全排列，每次设置first为第一行第一格数字，last为第一行最后一格数字，共$8!=40320$种结果，生成的结果作为新数独终局的第一行，重复上述流程

3.2.2. 数独问题的生成

ques_generate(ques_number)

题目生成的要求：

1. 棋盘上挖空不少于30个，不多于60个
2. 每个$3\times 3$棋盘中挖空不少于2个

通过3.2.1中生成的数独终局，使用随机挖空实现题目的生成：

1. 在每个$3\times 3$的方块中随机删除2个数字，以满足要求2，总共可以挖空18个
2. 生成一个12-42之间的随机数N作为剩余的挖空数量，继续从9x9的棋盘中不断挖空（与1中不重复）直到总挖空数量达到N

3.2.3 数独问题的解决

1. 使用深度优先搜索并结合剪枝：

2. 选定空位，遍历其所在行、所在列、所在$3\times 3$ 方格中的数字，排除不符合条件的数字

3. 数独终局的每一个位置，都代表递归过程中的一层，每次确定当前位置的数字之前，遍历当前行、当前列、以及当前3*3网格中的数字，排除不符合条件的数字，从而达到剪枝的目的

4. 剪枝的过程即对当前数独的合法性检查的过程，完成剪枝后继续对下一个位置进行检查直到完成

4 设计实现过程：

4.1 代码组织

4.1.1 类之间的关系

classDiagram
Sudoku --|> Solution
Sudoku --|> Question
Sudoku: str[] char     //一个数独终局或数独问题的输出字符串
Sudoku: str_board[][] char //一个数独问题的字符串二维数组
Question: Settle_ques() 
Solution: line[] char    //数独的第一行
Solution: final[][] char //输出的字符数组
Solution: sudoku_generate()
Question: ques_generate()

4.1.2 关键函数流程图

sudoku -c N

sudoku -p N

sudoku -s ques.txt

illegle input

N > 1

!N

N = 1

N > 1

!N

flag =EOF

flag !=EOF

main

sudoku_generate

ques_generate

settle_ques

Usage help

N--

!N

next_permutation

return

fputs

OUTPUT

N--

!N

fputs2

flag = fgetc

flag

return

DFS_settle

4.2 关键代码

4.2.1 数独终局的生成

static char AbsolutePath[100] = { 0 };	// 文件的相对路径
static char ques_board[10][20];	// 
static char buf[MAX]; // 输出
class Solution{
private:
    char line[9]={ '5','1','2','3','4','6','7','8','9' };
    char final[10][19];
    char str[200];
public:
    void sudoku_generate(int n){
        int cot = n，bit = 0;
        buf[0] = '\0';
        
        //char str[30];
        char line1[19] = { '5',' ','1', ' ' ,'2', ' ','3',' ','4', ' ','6',' ','7',' ','8',' ','9','\n','\0' };
        int shift[9] = { 0,6,12,2,8,14,4,10,16 };

        int pos1[6][3] = { { 3,4,5 },{ 3,5,4 },{ 4,5,3 },{ 4,3,5 },{ 5,4,3 },{ 5,3,4 } };
        int pos2[6][3] = { { 6,7,8 },{ 6,8,7 },{ 7,6,8 },{ 7,8,6 },{ 8,6,7 },{ 8,7,6 } };

        int flag = 0;
        int i,j,k;

        //初始值置空格和\0
        for (i = 0; i < 9; i++){
            for (j = 0; j < 17; j++){
                final[i][j] = ' ';
            }
            final[i][17] = '\n';
            final[i][18] = '\0';
        }
        final[9][0] = '\n';//第10行只有一个空行
        final[9][1] = '\0';

        FILE *fp = fopen(SUDOKUPATH, "w");
        //生成第一行
        do{
            for (i = 0; i < 9; i++){
                line1[2 * i] = line[i];
            }
            memcpy(final[0], line1, sizeof(line1));
            //以第一行为基础，生成一个终局
            for (i = 1; i < 9; i++){
                for (j = 0; j < 18; j += 2){
                    final[i][j] = line1[(j + shift[i]) % 18];
                }
            }
            //在一个终局的基础上改变4-6,7-9行的输出顺序即可
            for (i = 0; i < 6; i++){
                for (j = 0; j < 6; j++){
                    str[0] = '\0';
                    flag++;
                    //前三行
                    for (k = 0; k < 3; k++){
                        strcpy(buf + bit, final[k]);
                        bit += 18;
                    }
                    //3 4 5行
                    for (k = 0; k < 3; k++){
                        strcpy(buf + bit, final[pos1[i][k]]);
                        bit += 18;
                    }
                    //6 7 8行
                    for (k = 0; k < 3; k++){
                        strcpy(buf + bit, final[pos2[j][k]]);
                        bit += 18;
                    }
                    strcpy(buf + bit, "\n");
                    bit++;
                    if (n == 1){
                        buf[163 * (cot - 1) + 161] = '\0';
                        fputs(buf, fp);
                    }
                    n--;
                    if (!n) { fclose(fp); return; }
                }
            }

        }
        while (next_permutation(line + 1, line + 9));
    };
};

4.2.2 数独问题的生成

class Question{
private:
    char str[200];
public:
    void ques_generate(int ques_num){
        std::random_device rd;
        std::default_random_engine randomEngine(rd());
        std::uniform_int_distribution dis1(1,100);
        FILE *fpQues1;
        FILE *fpBase1;
        int num = 0;

        fpBase1 = fopen(SUDOKUPATH, "r");
        fpQues1 = fopen(QUESPATH, "w");
        ques_board[9][0] = '\n';
        ques_board[9][1] = '\0';
        while (ques_num--){
            str[0] = '\0';
            for (int i = 0; i < 9; i++){
                fgets(ques_board[i], 20, fpBase1);
            }
            if(fgetc(fpBase1) == -1){
                break;
            }
            //int base[9] = { 0,3,6,27,30,33,54,57,60 };
            int base[9] = { 0,6,12,54,60,66,108,114,120 };
            //int plus[9] = { 0,1,2,9,10,11,18,19,20 };
            int plus[9] = { 0,2,4,18,20,22,36,38,40 };
            //每个3*3随机掏空2个
            for (int k : base){
                int i, j, hole[2];//3*3里面掏的位置
                hole[0] = dis1(randomEngine)%9;
                hole[1] = dis1(randomEngine)%9;
                //防止重复
                while (hole[0] == hole[1]){
                    hole[1] = dis1(randomEngine) % 9;
                }
                for (int t : hole) {
                    int dot;
                    dot = k + plus[t];
                    i = dot / 18;
                    j = dot % 18;
                    ques_board[i][j] = '0';
                }
            }

            //已经掏空了18个
            int others;
            others = 12 + dis1(randomEngine) % 31;//再掏12-41个就可以了
            while (others--){
                int k = dis1(randomEngine) % 81;
                int i = k / 9;
                int j = k % 9;

                j *= 2;
                if (ques_board[i][j] != '0')
                    ques_board[i][j] = '0';
                else others++;
            }
            for (auto & i : ques_board){
                strcat(str, i);
            }
            if (!ques_num)
                str[161] = '\0';
            fputs(str, fpQues1);
        }
        fclose(fpBase1);
        fclose(fpQues1);
    }
};

4.2.3 数独问题的解决

void settle(int pos);
void settle_ques();
void prune(int i, int j, bool point[10]);

4.3 代码质量分析

代码质量分析工具：Clion集成基于clang的静态代码分析框架Clang-Tidy

4.3.1 使用

• 选择代码检查工具
  

• 设置代码检查范围
  

• 选择代码检查范围
  

• 代码检查结果
  

• 进行改进后，代码分析结果，显示没有错误

  

5 程序性能分析

程序性能分析工具：macOS（DTrace）上，Clion与CPU性能分析器集成

5.1 程序性能分析工具使用

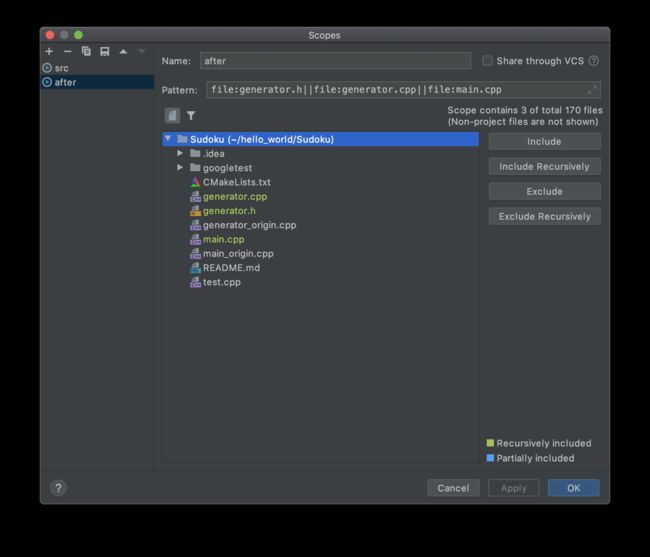
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0NKW45KT-1579447928427)(https://www.jetbrains.com/clion/features/img/2018.3/dynamic-analysis/profile_run.png)]

5.2 程序性能分析结果

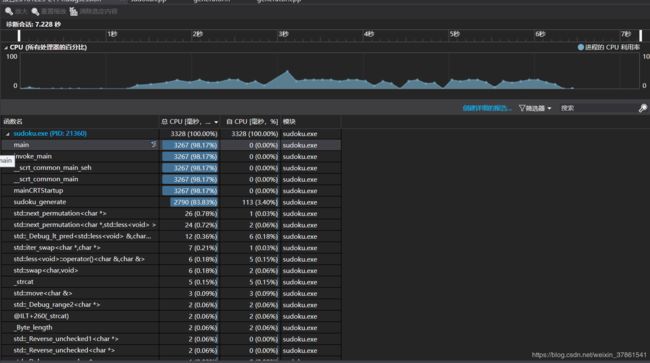
通过观察分析图可以发现，整个运行过程中，全排列占用的时间仅为0.78%，用于字符串连接的实践也仅有0.15%，说明大部分时间还是消耗在文件输出的过程中，如果要进行下一步的优化，还是应该针对输出部分做改进。

5.3 程序性能改进

5.3.1 针对文件输出的改进

• 通过对性能分析图的观察，发现整个数独生成过程中，全排列消耗的时间不到1%，而整个函数也没有其他多余的部分，说明，95%以上的时间消耗都是在输出过程中。于是，在输出之前，通过字符连接运算将每一个数字字符和空格和回车提前连接成一个字符串，于是一行只需要输出一次，使用freopen()和puts()，一个数独终局只需要输出10次，虽然运算代价稍有增加，程序运行时间仍然大大减少，从28s减少到了8s。性能得到了很大的优化。
• 二维数组存储81个数字，终局生成之后，采用freopen() 结合putchar() 对字符进行一个一个输出，在每个数字之后输出一个’\0’或者’\n’确保输出格式符合题目要求。通过这样的方式，一个数独终局需要输出163次，生成1e6个数独终局的时间为28s
• 继续在输出上做文章，前面的字符串连接主要是空格，但实际上可以把空格提前放入运算的数组中。一开始一位会很麻烦，但只要对代码进行微调就可以了，把循环变量的“i++”改成“i+=2”，同时其余细节进行稍微调整。最终采用freopen()和puts()一次输出一行，不需要进行字符串连接，最终时间是5.5s左右。
• 通过不断尝试，发现使用fopen()函数和fputs()会使得输出的时间稍微有所降低，但是效果不是很明显。
• 终局生成之后，在输出之前将整个熟读终局的所有字符连接成一个长的字符串，于是一个数独终局只需要输出一次。运行时间减少到了3.5s，当电脑状态好的情况下，可以跑进3s
• 在整个改进过程中，发现一个现象，当数组的每一行的所有字符都有效即每一行的末尾都没有’\0’字符的情况下，当用fputs()进行输出时，一次就可以将整个数独终局全部输出。因此有一个设想：使用得当的情况下，不需要进行将163个字符连接成一个长的字符串操作就可以直接输出，预计时间可以节省0.5s左右。但由于代码结构的原因，必须进行较大改动才能实现，故没有尝试。
• 开一个全局数组用于输出，将所有的终局都存进去，在最后需要输出的时候直接一次输出，最终生成1e6终局的时间在2.5s
• 生成1e6的高质量的数独终局10s以内就可以完成。

5.3.2 针对数独求解的性能改进

思路

数独的求解，根据数独终局的特性，最容易想到的就是深度优先搜索的暴力求解，并且代码比较简单，如果采用递归的话。
但很显然，这种解题方式解决少量题目的时候时间上不会有明显的差异。当当解决到1000题的时候，整个过程就会需要20多秒，因此剪枝就很有必要了

剪枝过程
对于数独终局的每一个位置，都代表递归过程中的一层，每次确定当前位置的数字之前，通过遍历当前行、当前列、以及当前3*3网格中的数字，就可以排除不符合条件的数字，从而达到剪枝的目的。
剪枝的过程其实已经完成了对当前数独的合法性的检查

剪枝效果
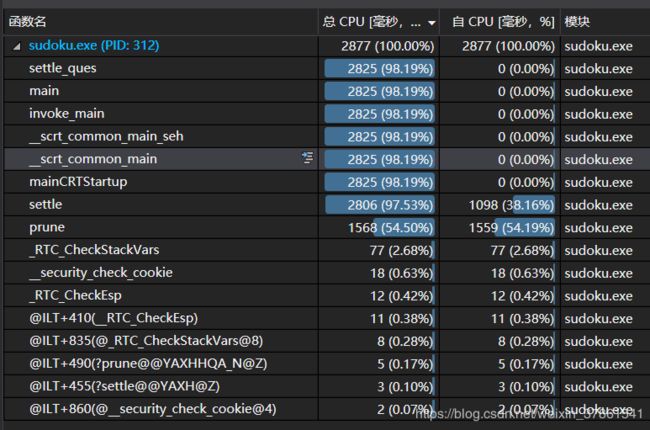
剪枝之后，解决1000题的运行时间减少了三分之二，从20s减少到了7s左右。

整个解题过程中，一半时间都是消耗在了剪枝，另外一半则消耗在深搜的部分。若是要继续优化，需要考虑不同的剪枝策略，在剪枝时间和效率之间取得一个平衡。

6 单元测试

6.1 单元测试设计

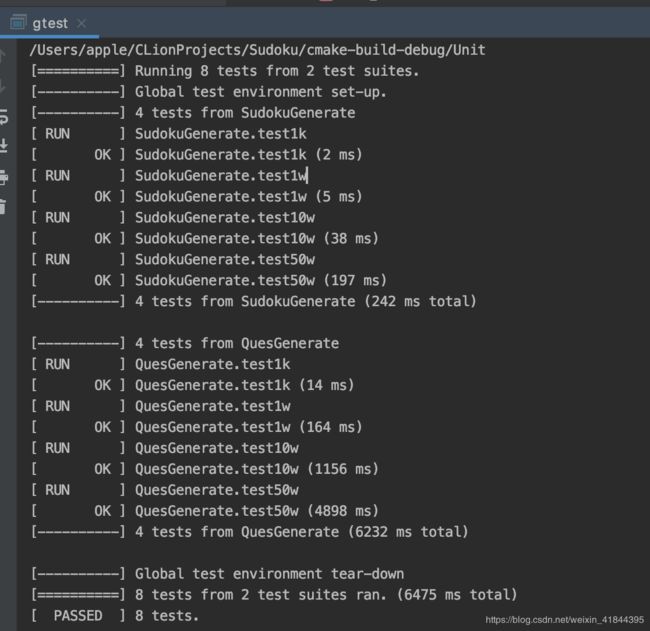
本例中测试目标为在不同规模下对生成数独、生成数独问题、数独问题解决这三个过程的时间进行测试

分别设计规模为1000、10000、100000、500000

6.2 单元测试用例

7 使用的外部库、插件、网址

• 图片超链接转换工具
• GoogleTest导入