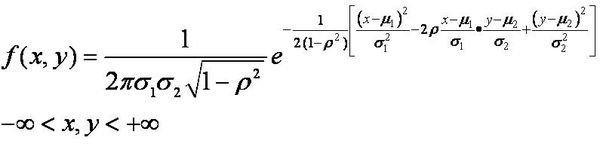【概率/数理统计】简单随机样本,抽样分布;卡方,T,F分布,正态总体的样本均值与方差分布;Γ函数(伽马函数/tao函数)
目录
1. 简单随机样本
2. 抽样分布
2. 正态分布
3. 卡方分布
4. T分布
5. F分布
6. 正态总体的样本均值与样本方差分布
7. 伽马函数
1. 简单随机样本
【简单随机样本】设 X 是具有分布函数 F 的随机变量,若 X1,X2,……Xn 是具有同一分布函数 F,相互独立的随机变量,则称 X1,X2,……Xn 是从分布函数 F (或称总体 F,或者总体 X)得到的容量为 n 的简单随机样本,简称样本。观察值x1,x2,...,xnx1,x2,...,xn称为样本值,也成为X的n个独立的观察值。(出自《概率论与数理统计》浙江大学 第四版)
注:样本,就是指简单随机样本,必满足 ① 与总体同分布,② 相互独立。
详见《总体与样本的理解》:https://blog.csdn.net/u011240016/article/details/52937371
2. 抽样分布
【抽样分布】统计量的分布是抽样分布。如卡方分布、T分布、F分布是几个来自正态总体的统计量的常用分布。
统计量就是不包含总体未知参数的、来自总体的样本的一个函数。
注:上一篇写的是在概率论范围内,离散型和连续型变量的分布,主要用于求分布算概率;这一篇是数理统计领域内(概率论的一个分支),抽样分布的情况,主要用于参数估计和推断统计。
下面首先重新介绍下正态分布。
2. 正态分布
2.1 一维正态分布
随机变量X服从正态分布,X~N(μ,σ^2),则密度函数为:
![]()
若服从标准正态分布,X~N(0,1),则密度函数为:
![]()
2.2 二维正态分布
(X, Y)~![]() ,其中 ρ 是线性相关系数。
,其中 ρ 是线性相关系数。
当X,Y独立时(此条件可退化为 “X, Y不相关” ),ρ=0,此时简化为下式。
注:此时的边缘分布是一维正态分布。
3. 卡方分布
设 X1, X2, ……Xn 是来自总体 N(0, 1) 的样本,则称下面的统计量服从自由度为 n 的卡方分布,即 ![]() 。
。
![]()
性质:
- 可加性:
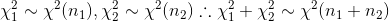
- E(卡方)=n, D(卡方)=2n。
4. T分布
设 X~N(0, 1), Y~X^2(n),且相互独立,则统计量t服从自由度为 n 的 t 分布,记为 t~t(n)。
- 分位点的性质:
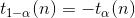
5. F分布
设 U~X^2(n1), V~X^2(n2),且相互独立,则统计量F服从自由度(n1,n2)的F分布,记为 F~F(n1, n2)。
6. 正态总体的样本均值与样本方差分布
设总体X存在均值μ,方差σ^2,不管总体是什么分布,X1,……Xn 是来自X的一个样本,X拔 ,S^2 分别是样本均值和样本方差,则
E(X拔)=μ,D(X拔)=(σ^2)/n,E(S^2)=σ^2
并有如下定理:
7. 伽马函数
卡方分布的概率密度函数和 Γ 分布有关,但是不用掌握,不过需要区分一下两个概念。伽马分布和伽马函数是不同的,伽马函数需要记忆。
相关性质:
- ① Γ(1)=1
- ② Γ(x+1)= x Γ(x)
- ③ Γ(n)=(n-1)!
- ④ Γ(x) Γ(1-x)=pai/sin(pai x)
- ⑤ Γ(1/2)=根号pai
《第八章tao函数》:http://www.doc88.com/p-7856207317036.html
伽马函数也称 tao 函数,具体性质及推导可见此文。
《伽马分布》:http://www.360doc.com/content/18/0315/17/51704_737276354.shtml
这里的伽马分布是与伽马函数不同的,注意区分。文中指出了伽马分布和其他分布的关系,公式有的无法加载。