雷达原理(第五版)常见公式
第 1 章 绪论
1.1.1 雷达回波中的可用信息

R : 斜 距 , 雷 达 到 目 标 的 直 线 距 离 R : 斜距,雷达到目标的直线距离 R:斜距,雷达到目标的直线距离
H : 目 标 距 水 平 面 的 高 度 H : 目标距水平面的高度 H:目标距水平面的高度
D : 水 平 距 离 D : 水平距离 D:水平距离
α : 方 位 角 , 目 标 斜 距 R 在 水 平 面 的 投 影 与 某 一 起 始 方 向 在 水 平 面 的 夹 角 \alpha : 方位角,目标斜距R在水平面的投影与某一起始方向在水平面的夹角 α:方位角,目标斜距R在水平面的投影与某一起始方向在水平面的夹角
β : 仰 角 , 斜 距 与 水 平 面 的 夹 角 \beta : 仰角,斜距与水平面的夹角 β:仰角,斜距与水平面的夹角
D = R cos β H = R sin β α = α \begin{aligned} D&=R\cos\beta\\ H&=R\sin\beta\\ \alpha&=\alpha \end{aligned} DHα=Rcosβ=Rsinβ=α
R : 目 标 到 雷 达 的 单 程 距 离 R : 目标到雷达的单程距离 R:目标到雷达的单程距离
c : 光 速 , ( c = 3 × 1 0 8 ( m / s ) ) c : 光速,(c=3\times10^8(m/s)) c:光速,(c=3×108(m/s))
t r : 电 磁 波 往 返 于 目 标 与 雷 达 之 间 的 时 间 间 隔 , ( 1 μ s = 1 × 1 0 − 6 s ) t_{r} : 电磁波往返于目标与雷达之间的时间间隔,(1\mu s=1\times10^{-6}s) tr:电磁波往返于目标与雷达之间的时间间隔,(1μs=1×10−6s)
R = c t r 2 R=\frac{ct_{r}}{2} R=2ctr
f d : 多 普 勒 频 移 , ( H z ) f_{d} : 多普勒频移,(Hz) fd:多普勒频移,(Hz)
v r : 雷 达 与 目 标 之 间 的 径 向 速 度 , ( m / s ) v_{r} : 雷达与目标之间的径向速度,(m/s) vr:雷达与目标之间的径向速度,(m/s)
λ : 载 波 波 长 , ( m ) \lambda : 载波波长,(m) λ:载波波长,(m)
f d = 2 v r λ = 2 v r cos θ λ ( 有 夹 角 时 ) \begin{aligned} f_{d}&=\frac{2v_{r}}{\lambda}\\ &=\frac{2v_{r}\cos\theta}{\lambda}\qquad(有夹角时) \end{aligned} fd=λ2vr=λ2vrcosθ(有夹角时)
1.1.2 基本雷达方程
P t : 雷 达 发 射 机 功 率 P_{t} : 雷达发射机功率 Pt:雷达发射机功率
G : 天 线 增 益 G : 天线增益 G:天线增益
R : 雷 达 与 目 标 的 距 离 R : 雷达与目标的距离 R:雷达与目标的距离
S 1 : 雷 达 照 射 到 目 标 的 功 率 密 度 S_{1} : 雷达照射到目标的功率密度 S1:雷达照射到目标的功率密度
σ : 雷 达 截 面 积 \sigma : 雷达截面积 σ:雷达截面积
S 2 : 雷 达 照 射 到 目 标 , 反 射 回 雷 达 的 功 率 密 度 S_{2} : 雷达照射到目标,反射回雷达的功率密度 S2:雷达照射到目标,反射回雷达的功率密度
A e : 天 线 的 有 效 接 受 面 积 A_{e} : 天线的有效接受面积 Ae:天线的有效接受面积
λ : 载 波 波 长 , ( m ) \lambda : 载波波长,(m) λ:载波波长,(m)
P r : 回 波 功 率 P_{r} : 回波功率 Pr:回波功率
S m i n : 最 小 可 检 测 信 号 , ( S m i n ∈ P r ) S_{min} : 最小可检测信号,(S_{min} \in P_{r}) Smin:最小可检测信号,(Smin∈Pr)
R m a x : 雷 达 最 大 作 用 距 离 , ( R m a x ∈ R ) R_{max} : 雷达最大作用距离,(R_{max} \in R) Rmax:雷达最大作用距离,(Rmax∈R)
G = 4 π A e λ 2 G=\frac{4\pi A_{e}}{\lambda^2} G=λ24πAe
S 1 = P t 4 π R 2 S 2 = S 1 σ 4 π R 2 = P t 4 π R 2 ⋅ σ 4 π R 2 P r = A e S 2 = P t G A e σ ( 4 π ) 2 R 4 \begin{aligned} S_{1}&=\frac{P_{t}}{4\pi R^2}\\ S_{2}&=S_{1}\frac{\sigma}{4\pi R^2}=\frac{P_{t}}{4\pi R^2}\cdot\frac{\sigma}{4\pi R^2}\\ P_{r}&=A_{e}S_{2}=\frac{P_{t}GA_{e}\sigma}{(4\pi)^2R^4}\\ \end{aligned} S1S2Pr=4πR2Pt=S14πR2σ=4πR2Pt⋅4πR2σ=AeS2=(4π)2R4PtGAeσ
R m a x = [ P t G A e σ ( 4 π ) 2 S m i n ] 1 / 4 ( P r = S m i n ) = [ P t G 2 λ 2 σ ( 4 π ) 3 S m i n ] 1 / 4 ( G = 4 π A e λ 2 ) = [ P t A e 2 σ 4 π λ 2 S m i n ] 1 / 4 ( G = 4 π A e λ 2 ) \begin{aligned} R_{max}&=\left[\frac{P_{t}GA_{e}\sigma}{(4\pi)^2S_{min}}\right]^{1/4}\qquad(P_{r}=S_{min})\\ &=\left[\frac{P_{t}G^2\lambda^2\sigma}{(4\pi)^3S_{min}}\right]^{1/4}\qquad(G=\frac{4\pi A_{e}}{\lambda^2})\\ &=\left[\frac{P_{t}A_{e}^2\sigma}{4\pi\lambda^2S_{min}}\right]^{1/4}\qquad(G=\frac{4\pi A_{e}}{\lambda^2}) \end{aligned} Rmax=[(4π)2SminPtGAeσ]1/4(Pr=Smin)=[(4π)3SminPtG2λ2σ]1/4(G=λ24πAe)=[4πλ2SminPtAe2σ]1/4(G=λ24πAe)
第 2 章 雷达发射机
2.2.2 输出功率
P t : 峰 值 功 率 , 脉 冲 期 间 射 频 振 荡 的 平 均 功 率 P_{t} : 峰值功率,脉冲期间射频振荡的平均功率 Pt:峰值功率,脉冲期间射频振荡的平均功率
P a v : 平 均 功 率 , 脉 冲 重 复 周 期 内 的 输 出 功 率 的 平 均 值 P_{av} : 平均功率,脉冲重复周期内的输出功率的平均值 Pav:平均功率,脉冲重复周期内的输出功率的平均值
f r : 重 复 频 率 f_{r} : 重复频率 fr:重复频率
τ : 脉 冲 宽 度 \tau : 脉冲宽度 τ:脉冲宽度
T r : 脉 冲 重 复 周 期 T_{r} : 脉冲重复周期 Tr:脉冲重复周期
D : 工 作 比 / 占 空 比 D : 工作比/占空比 D:工作比/占空比
f r = 1 T r D = τ T r P a v = P t ⋅ D = P t τ T r \begin{aligned} f_{r}&=\frac{1}{T_{r}}\\ D&=\frac{\tau}{T_{r}}\\ P_{av}&=P_{t} \cdot D=P_{t}\frac{\tau}{T_{r}} \end{aligned} frDPav=Tr1=Trτ=Pt⋅D=PtTrτ
2.2.4 频谱纯度
Δ B : 带 宽 \Delta B : 带宽 ΔB:带宽
L ( f m ) = 10 × lg Δ B 带 宽 内 的 单 边 带 功 率 信 号 功 率 × Δ B L(f_{m})=10\times\lg\frac{\Delta B带宽内的单边带功率}{信号功率 \times \Delta B} L(fm)=10×lg信号功率×ΔBΔB带宽内的单边带功率
第 3 章 雷达接收机
3.2.1 噪声系数和灵敏度
S i : 输 入 信 号 功 率 S_{i} : 输入信号功率 Si:输入信号功率
N i : 输 入 噪 声 功 率 N_{i} : 输入噪声功率 Ni:输入噪声功率
S o : 输 出 信 号 功 率 S_{o} : 输出信号功率 So:输出信号功率
N o : 输 出 噪 声 功 率 N_{o} : 输出噪声功率 No:输出噪声功率
F : 噪 声 系 数 F : 噪声系数 F:噪声系数
F = S i / N i S o / N o F=\frac{S_{i}/N_{i}}{S_{o}/N_{o}} F=So/NoSi/Ni
k : 玻 尔 兹 曼 常 数 , ( k ≈ 1.38 × 1 0 − 23 ) j / K k : 玻尔兹曼常数,(k \approx 1.38 \times 10^{-23})j/K k:玻尔兹曼常数,(k≈1.38×10−23)j/K
T o : 热 力 学 温 度 , T o = 290 K ( 1 7 ∘ C ) T_{o} : 热力学温度,T_{o}=290K(17^\circ C) To:热力学温度,To=290K(17∘C)
B n : 系 统 噪 声 带 宽 B_{n} : 系统噪声带宽 Bn:系统噪声带宽
M : 识 别 系 数 ( 临 界 灵 敏 度 → M = 1 ) M : 识别系数(临界灵敏度 \to M=1) M:识别系数(临界灵敏度→M=1)
S i m i n = k T o B n F M S_{imin}=kT_{o}B_{n}FM Simin=kToBnFM
3.4.2 噪声系数和温度
(1) 噪声系数
G a : 接 收 机 的 额 定 功 率 增 益 G_{a} : 接收机的额定功率增益 Ga:接收机的额定功率增益
Δ N : 接 收 机 内 部 噪 声 在 输 出 端 所 呈 现 的 额 定 噪 声 功 率 \Delta N : 接收机内部噪声在输出端所呈现的额定噪声功率 ΔN:接收机内部噪声在输出端所呈现的额定噪声功率
F = N o N i G a N o = N i G a + Δ N = k T 0 B n G a + Δ N F = 1 + Δ N k T 0 B n G a = 1 G a ( 无 源 或 有 源 四 端 网 络 ) \begin{aligned} F&=\frac{N_{o}}{N_{i}G_{a}}\\ N_{o}&=N_{i}G_{a}+\Delta N=kT_{0}B_{n}G_{a}+\Delta N\\ F&=1+\frac{\Delta N}{kT_{0}B_{n}G_{a}}\\ &=\frac{1}{G_{a}} \qquad (无源或有源四端网络) \end{aligned} FNoF=NiGaNo=NiGa+ΔN=kT0BnGa+ΔN=1+kT0BnGaΔN=Ga1(无源或有源四端网络)
(2) 等效噪声温度
T A : 天 线 噪 声 温 度 T_{A} : 天线噪声温度 TA:天线噪声温度
N A : 接 收 机 外 部 噪 声 的 额 定 功 率 N_{A} : 接收机外部噪声的额定功率 NA:接收机外部噪声的额定功率
T e : 等 效 噪 声 温 度 T_{e} : 等效噪声温度 Te:等效噪声温度
T s : 系 统 噪 声 温 度 T_{s} : 系统噪声温度 Ts:系统噪声温度
N A = k T A B n Δ N = k T e B n G a F = 1 + T e T 0 T e = ( F − 1 ) T 0 = ( F − 1 ) × 290 ( K ) T s = T A + T e \begin{aligned} N_{A}&=kT_{A}B_{n}\\ \Delta N&=kT_{e}B_{n}G_{a}\\ F&=1+\frac{T_{e}}{T_{0}}\\ T_{e}&=(F-1)T_{0}=(F-1) \times 290(K)\\ T_{s}&=T_{A}+T_{e} \end{aligned} NAΔNFTeTs=kTABn=kTeBnGa=1+T0Te=(F−1)T0=(F−1)×290(K)=TA+Te
(3) 相对噪声温度——噪声比
t c = F c k T 0 B n G c k T 0 B n = F c G c t_{c}=\frac{F_{c}kT_{0}B_{n}G_{c}}{kT_{0}B_{n}}=F_{c}G_{c} tc=kT0BnFckT0BnGc=FcGc
3.4.3 级联电路的噪声系数
F 0 : 接 收 机 总 噪 声 系 数 F_{0} : 接收机总噪声系数 F0:接收机总噪声系数
F n : 第 n 级 电 路 的 噪 声 系 数 F_{n} : 第 n 级电路的噪声系数 Fn:第n级电路的噪声系数
G n : 第 n 级 电 路 的 额 定 功 率 增 益 G_{n} : 第 n 级电路的额定功率增益 Gn:第n级电路的额定功率增益
F 0 = F 1 + F 2 − 1 G 1 + F 3 − 1 G 1 G 2 + ⋯ + F n − 1 G 1 G 2 ⋯ G n − 1 F 0 = 1 G f G g G l ( F R + F c − 1 G R + F l − 1 G R G c ) ( 前 三 部 分 F = 1 G ) \begin{aligned} F_{0}&=F_{1}+\frac{F_{2}-1}{G_{1}}+\frac{F_{3}-1}{G_{1}G_{2}}+ \cdots +\frac{F_{n}-1}{G_{1}G_{2} \cdots G_{n-1}}\\ F_{0}&=\frac{1}{G_{f}G_{g}G_{l}}\left(F_{R}+\frac{F_{c}-1}{G_{R}}+\frac{F_{l}-1}{G_{R}G_{c}}\right) \qquad (前三部分 \quad F=\frac{1}{G}) \end{aligned} F0F0=F1+G1F2−1+G1G2F3−1+⋯+G1G2⋯Gn−1Fn−1=GfGgGl1(FR+GRFc−1+GRGcFl−1)(前三部分F=G1)
3.4.4 接收机灵敏度
S i m i n : 接 收 机 灵 敏 度 ( 最 小 可 检 测 信 号 功 率 ) , M = 1 S_{imin} : 接收机灵敏度(最小可检测信号功率),M=1 Simin:接收机灵敏度(最小可检测信号功率),M=1
f r : 重 复 频 率 f_{r} : 重复频率 fr:重复频率
R : 最 大 的 单 值 测 距 范 围 R : 最大的单值测距范围 R:最大的单值测距范围
R = c 2 f r B = 最 佳 带 宽 脉 宽 积 脉 冲 宽 度 S i m i n ( d B m ) = − 114 ( d B ) + 10 lg B n ( M H z ) + 10 lg F ( F : 内 外 噪 声 系 数 ) \begin{aligned} R&=\frac{c}{2f_{r}}\\ B&=\frac{最佳带宽脉宽积}{脉冲宽度}\\ S_{imin}(dBm)&=-114(dB)+10\lg B_{n}(MHz)+10\lg F \qquad (F:内外噪声系数) \end{aligned} RBSimin(dBm)=2frc=脉冲宽度最佳带宽脉宽积=−114(dB)+10lgBn(MHz)+10lgF(F:内外噪声系数)
第 5 章 雷达作用距离
5.1 雷达方程
5.1.1 基本雷达方程
详情请看 1.1.2
5.1.2 目标雷达截面积(RCS)
σ : 目 标 的 雷 达 截 面 积 \sigma: 目标的雷达截面积 σ:目标的雷达截面积
P 2 : 目 标 散 射 的 总 功 率 P_{2}: 目标散射的总功率 P2:目标散射的总功率
S 1 : 照 射 的 功 率 密 度 ( 目 标 处 入 射 的 功 率 密 度 ) S_{1}: 照射的功率密度(目标处入射的功率密度) S1:照射的功率密度(目标处入射的功率密度)
P Δ : 雷 达 接 收 点 处 单 位 立 体 角 内 的 散 射 功 率 P_{\Delta}: 雷达接收点处单位立体角内的散射功率 PΔ:雷达接收点处单位立体角内的散射功率
P Δ = P 2 4 π = S 1 σ 4 π σ = P 2 S 1 = 4 π p Δ S 1 \begin{aligned} P_{\Delta}&=\frac{P_{2}}{4\pi}=S_{1}\frac{\sigma}{4\pi}\\ \sigma&=\frac{P_{2}}{S_{1}}\\ &=4\pi\frac{p_{\Delta}}{S_{1}} \end{aligned} PΔσ=4πP2=S14πσ=S1P2=4πS1pΔ
5.2 最小可检测信号
5.2.1 最小可检测信噪比
G a : 接 收 机 的 功 率 增 益 ( 有 效 增 益 ) G_{a}: 接收机的功率增益(有效增益) Ga:接收机的功率增益(有效增益)
F n : 接 收 机 的 噪 声 系 数 F_{n}: 接收机的噪声系数 Fn:接收机的噪声系数
N : 接 收 机 输 出 的 噪 声 功 率 N: 接收机输出的噪声功率 N:接收机输出的噪声功率
N 0 : 噪 声 功 率 谱 密 度 N_{0}: 噪声功率谱密度 N0:噪声功率谱密度
τ : 波 形 宽 度 \tau: 波形宽度 τ:波形宽度
E r : 接 收 信 号 能 量 E_{r}: 接收信号能量 Er:接收信号能量
D 0 : 检 测 因 子 ( 最 小 输 出 信 噪 比 ) D_{0}: 检测因子(最小输出信噪比) D0:检测因子(最小输出信噪比)
G a = S 0 S i F n = N k T 0 B n G a S N = S N 0 B n = S τ N 0 = E r N 0 ( 简 单 脉 冲 B n ≈ 1 / τ ) D 0 = ( E r N 0 ) o m i n = ( S N ) 0 m i n \begin{aligned} G_{a}&=\frac{S_{0}}{S_{i}}\\ F_{n}&=\frac{N}{kT_{0}B_{n}G_{a}}\\ \frac{S}{N}&=\frac{S}{N_{0}B_{n}}=\frac{S\tau}{N_{0}}=\frac{E_{r}}{N_{0}}\qquad(简单脉冲 B_{n}\approx 1/\tau)\\ D_{0}&=\left(\frac{E_{r}}{N_{0}}\right)_{omin}=\left(\frac{S}{N}\right)_{0 min} \end{aligned} GaFnNSD0=SiS0=kT0BnGaN=N0BnS=N0Sτ=N0Er(简单脉冲Bn≈1/τ)=(N0Er)omin=(NS)0min
5.2.2 门限检测
P d : 发 现 概 率 , 目 标 存 在 且 判 断 有 P_{d}: 发现概率,目标存在且判断有 Pd:发现概率,目标存在且判断有
P l a : 漏 报 概 率 , 目 标 存 在 且 判 断 无 P_{la}: 漏报概率,目标存在且判断无 Pla:漏报概率,目标存在且判断无
P a n : 正 确 不 发 现 概 率 , 目 标 不 存 在 且 判 断 无 P_{an}: 正确不发现概率,目标不存在且判断无 Pan:正确不发现概率,目标不存在且判断无
P f a : 虚 警 概 率 , 目 标 不 存 在 且 判 断 有 P_{fa}: 虚警概率,目标不存在且判断有 Pfa:虚警概率,目标不存在且判断有
P d + P l a = 1 P a n + P f a = 1 \begin{aligned} P_{d}+P_{la}&=1\\ P_{an}+P_{fa}&=1 \end{aligned} Pd+PlaPan+Pfa=1=1
5.2.3 检测性能和信噪比
(1) 虚警概率
U T : 门 限 电 平 U_{T}: 门限电平 UT:门限电平
P f a = exp ( − U T 2 2 σ 2 ) P_{fa}=\exp\left(-\frac{U_{T}^2}{2\sigma^2}\right) Pfa=exp(−2σ2UT2)
(2)发现概率
I 0 : 宗 量 z 的 0 阶 修 正 贝 塞 尔 函 数 I_{0}: 宗量 z 的 0 阶修正贝塞尔函数 I0:宗量z的0阶修正贝塞尔函数
P d = ∫ U T ∞ r σ 2 exp ( − r 2 + A 2 2 σ 2 ) I 0 ( r A σ 2 ) d r P_{d}=\int_{U_{T}}^{\infty}\frac{r}{\sigma^2}\exp\left(-\frac{r^2+A^2}{2\sigma^2}\right)I_{0}\left(\frac{rA}{\sigma^2}\right)dr Pd=∫UT∞σ2rexp(−2σ2r2+A2)I0(σ2rA)dr
A σ = ( 2 S N ) 1 / 2 U T 2 2 σ 2 = ln 1 P f a \begin{aligned} \frac{A}{\sigma}&=\left(\frac{2S}{N}\right)^{1/2}\\ \frac{U_{T}^2}{2\sigma^2}&=\ln\frac{1}{P_{fa}} \end{aligned} σA2σ2UT2=(N2S)1/2=lnPfa1
5.4.5 目标起伏模型
施威林起伏模型(Swerling)
适合大量近似相等单元散射体组成情况
(1) 施威林 I 型,慢起伏,瑞利分布
(2) 施威林 II 型,快起伏,瑞利分布
P ( σ ) = 1 σ ‾ exp ( − σ σ ‾ ) P(\sigma)=\frac{1}{\overline{\sigma}}\exp(-\frac{\sigma}{\overline{\sigma}}) P(σ)=σ1exp(−σσ)
适合较大反射体和许多小反射体合成
(3) 施威林 IIII 型,慢起伏
(4) 施威林 IV 型,慢起伏
P ( σ ) = 4 σ σ ‾ 2 exp ( − 2 σ σ ‾ ) P(\sigma)=\frac{4\sigma}{\overline{\sigma}^2}\exp(-\frac{2\sigma}{\overline{\sigma}}) P(σ)=σ24σexp(−σ2σ)
特别提示: 做题大部分看表和图(P202,P204,P205)
第 6 章 目标距离的测量
R : 目 标 到 雷 达 站 的 距 离 R: 目标到雷达站的距离 R:目标到雷达站的距离
c : 无 线 电 速 度 ( 光 速 c = 3 × 1 0 8 m / s ) c: 无线电速度(光速c=3\times10^8 m/s) c:无线电速度(光速c=3×108m/s)
t R : 往 返 一 次 时 间 t_{R}: 往返一次时间 tR:往返一次时间
t R = 2 R c R = 1 2 c t R \begin{aligned} t_{R}&=\frac{2R}{c}\\ R&=\frac{1}{2}ct_{R} \end{aligned} tRR=c2R=21ctR
第 7 章 角度测量
7.2.1 相位测角
φ = 2 π λ Δ R = 2 π λ d sin θ \varphi=\frac{2\pi}{\lambda}\Delta R=\frac{2\pi}{\lambda}d\sin\theta φ=λ2πΔR=λ2πdsinθ
7.3.2 天线波束的扫描方法
(1)栅瓣条件
d λ < 1 1 + ∣ sin θ 0 ∣ < 1 2 sin θ m a x \begin{aligned} \frac{d}{\lambda}&\lt \frac{1}{1+|\sin\theta_{0}|}\\ &\lt \frac{1}{2\sin\theta_{max}} \end{aligned} λd<1+∣sinθ0∣1<2sinθmax1
θ 0.5 ≈ 0.886 N d λ ( r a d ) ≈ 50.8 N d λ ( ∘ ) \theta_{0.5}\approx \frac{0.886}{Nd}\lambda (rad)\approx\frac{50.8}{Nd}\lambda (^\circ) θ0.5≈Nd0.886λ(rad)≈Nd50.8λ(∘)
7.6 三坐标雷达
V : 雷 达 待 测 空 域 立 体 角 V: 雷达待测空域立体角 V:雷达待测空域立体角
θ : 波 速 宽 度 立 体 角 \theta: 波速宽度立体角 θ:波速宽度立体角
T r : 雷 达 重 复 周 期 T_{r}: 雷达重复周期 Tr:雷达重复周期
f r : 重 复 频 率 f_{r}: 重复频率 fr:重复频率
N : 回 波 脉 冲 数 N: 回波脉冲数 N:回波脉冲数
D : 雷 达 的 数 据 率 D: 雷达的数据率 D:雷达的数据率
T s = V θ N T r = V θ N f r t r m a x = 2 R m a x c D = 1 T s = θ V 1 N T r = θ f r V N \begin{aligned} T_{s}&=\frac{V}{\theta}NT_{r}=\frac{V}{\theta}\frac{N}{f_{r}}\\ t_{rmax}&=\frac{2R_{max}}{c}\\ D&=\frac{1}{T_{s}}=\frac{\theta}{V}\frac{1}{NT_{r}}=\frac{\theta f_{r}}{VN} \end{aligned} TstrmaxD=θVNTr=θVfrN=c2Rmax=Ts1=VθNTr1=VNθfr
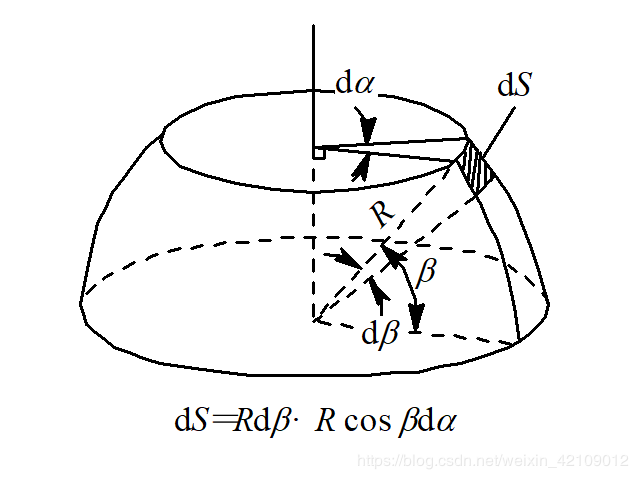
S : 待 测 空 域 所 截 球 面 面 积 S: 待测空域所截球面面积 S:待测空域所截球面面积
R : 球 半 径 R: 球半径 R:球半径
波 速 宽 度 θ α , θ β 不 相 等 ⟹ θ = θ α θ β / 2 波速宽度\theta_{\alpha},\theta_{\beta}不相等\Longrightarrow \theta=\theta_{\alpha}\theta_{\beta}/2 波速宽度θα,θβ不相等⟹θ=θαθβ/2
待 测 空 域 的 方 位 范 围 α 1 ∼ α 2 , 仰 角 范 围 β 1 ∼ β 2 待测空域的方位范围\alpha_{1}\sim\alpha_{2},仰角范围\beta_{1}\sim\beta_{2} 待测空域的方位范围α1∼α2,仰角范围β1∼β2
V = S R 2 = 1 R 2 ∬ d S = 1 R 2 ∫ α 1 α 2 ∫ β 1 β 2 R 2 cos β d α d β = ( α 2 − α 1 ) ( sin β 2 − sin β 1 ) ( r a d ) \begin{aligned} V&=\frac{S}{R^2}=\frac{1}{R^2}\iint dS\\ &=\frac{1}{R^2}\int_{\alpha_{1}}^{\alpha_{2}}\int_{\beta_{1}}^{\beta_{2}}R^2\cos\beta d\alpha d\beta\\ &=(\alpha_{2}-\alpha_{1})(\sin\beta_{2}-\sin\beta_{1}) \qquad(rad) \end{aligned} V=R2S=R21∬dS=R21∫α1α2∫β1β2R2cosβdαdβ=(α2−α1)(sinβ2−sinβ1)(rad)
结语:很杂

