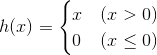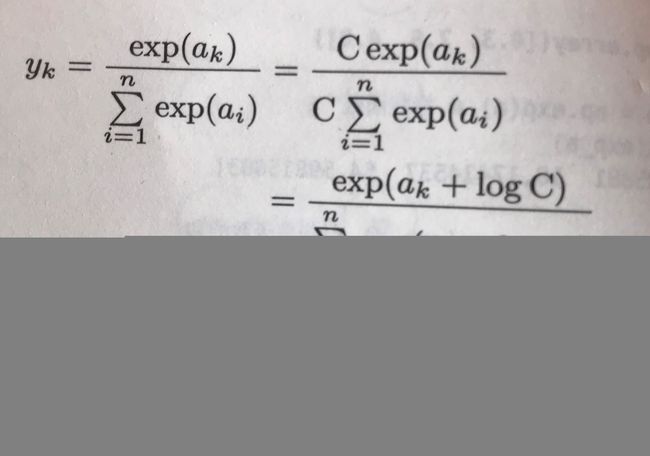第三章神经网络——基于numpy的代码详解

本专栏是书《深度学习入门》的阅读笔记一共八章：

第一章深度学习中的Python基础。主要讲解了深度学习将要用到的python的基础知识以及简单介绍了numpy库和matpoltlib库，本书编写深度学习神经网络代码仅使用Python和numpy库，不使用目前流行的各种深度学习框架，适合入门新手学习理论知识。

第二章感知机。主要介绍了神经网络和深度学习的基本单元感知机。感知机接收多个输入，产生一个输出，单层感知器可以实现与门，或门以及与非门，但是不能实现异或门，异或门的实现需要借助多层感知机，这也就是说，单层感知机只能表示线性空间，而非线性空间的表示需要借助多层感知机。

第三章神经网络

    上一章我们知道了，多层感知机理论上可以表示任何函数，甚至可以实现复杂的计算机，但是，截止目前为止，确定感知机的权重和偏置都是由人工计算得到的，对于多层感知机，人工确定权重和偏置的方法未免也太太太麻烦了，所以，神经网络的作用就是能够让网络自身进行学习权重和偏置，遗憾的是本章不打算介绍神经网络的学习算法，本章主要介绍神经网络的结构，神经网络的学习算法由下一章给出。

3.1激活函数

    感知机与神经网络的区别就在于激活函数，可以说，感知机就是激活函数选用了阶跃函数的神经网络，除了激活函数，其他方面比如神经元的多层连接的构造、信号的传递方法等感知机和神经网络都大致相同。

3.1.1阶跃函数

    用Python实现阶跃函数的代码为：

import numpy as np
def step_function(x):
    y=x>0#对输入的np数组进行不等式运算，得到y是一个布尔型数组
    return y.astype(np.int)#将布尔型数组y转换成int型数组，其中Ture转换为1
    #astype()函数通过参数指定期望的类型

函数图像： 

3.1.2sigmoid函数

sigmoid函数的数学表达式为：

用Python编写sigmoid函数的代码为：

import numpy as np
def sigmoid(x):
    return 1/(1+np.exp(-x))

因为numpy具有广播的作用，所以可以直接输入numpy数组x并产生一个和x同样维度的数组。

函数图像 

3.1.3ReLU函数

ReLU函数的数学表达式为：

ReLU的Python代码为：

import numpy as np
def ReLU(x):
    return np.maximum(0,x)

函数图像：

3.1.4非线性函数

这里强调一点，神经网络的激活函数必须使用非线性函数，因为如果使用线性函数的话，加深网络的意义就消失了。我们用一个简单的例子来说明，假如激活函数,那么一个三层的网络可以写成，而我们可以用来代替c，那么三层网络就失去了层数多的意义。使用线性函数时，无法发挥多层网络带来的优势。因此，为了发挥叠加层所带来的优势，激活函数必须使用非线性函数。

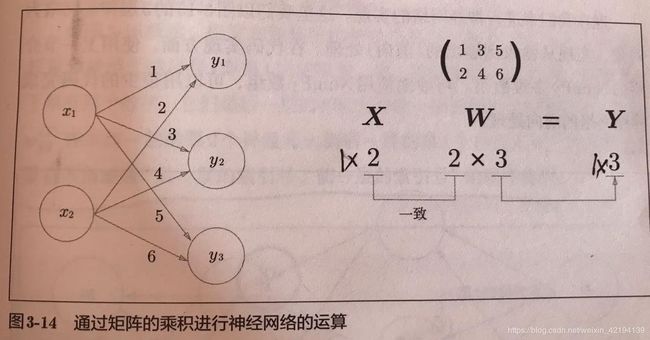
3.2神经网络中的矩阵乘法

    我们用下面的图来表示一层神经网络的计算：

    用Python的实现代码为：

import numpy as np
X=np.array([1,2])
W=np.array([[1,3,5],[2,4,6]])
Y=np.dot(X,W)

3.3 三层神经网络的代码

import numpy as np

def init_network:
    network={}
    #第一层
    network['W1']=np,array([[1,2,3],[4,5,6]])#两个输入，第一层隐藏层有3个神经元
    network['b1']=np,array([1,1,1])#该隐藏层有3个神经元
    #第二层
    network['W2']=np,array([[1,5],[2,6],[3,8]])#第一层隐藏层有3个神经元，该隐藏层有2个神经元
    network['b2']=np,array([2,2])#该隐藏层有2个神经元
    #第三层
    network['W3']=np,array([[1,2],[3,4]])#上一层隐藏层有两个神经元，输出层有两个神经元
    network['b3']=np,array([3,3])#该层有2个神经元
    
    return network

def forword(network,x):
    #提取神经网络参数
    W1=network['W1']
    b1=network['b1']
    W2=network['W2']
    b2=network['b2']
    W3=network['W3']
    b3=network['b3']
    #前向传播
    a1=np.dot(x,W1)+b1#第一个隐藏层
    z1=sigmoid(a1)#第一个隐藏层的激活函数是sigmoid
    a2=np.dot(z1,W2)+b2#第二个隐藏层
    z2=sigmoid(a2)#第二个隐藏层的激活函数是sigmoid
    a3=np.dot(z2,W3)+b3#输出层
    y=a3#输出层激活函数是恒等函数

    return y

network=init_network
x=np.array([1,2])
y=forword(network,x)

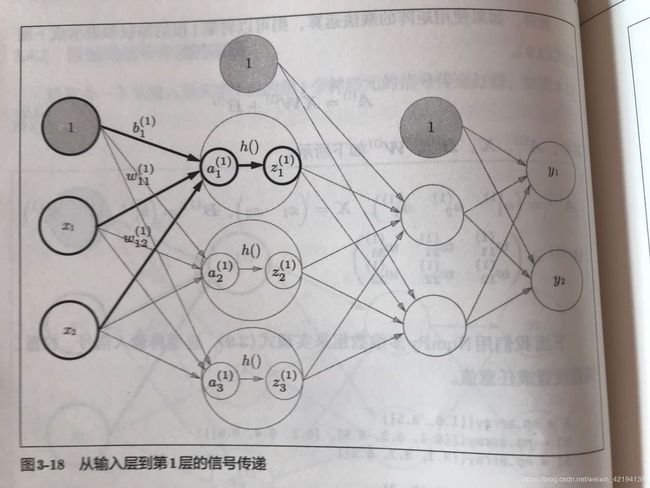
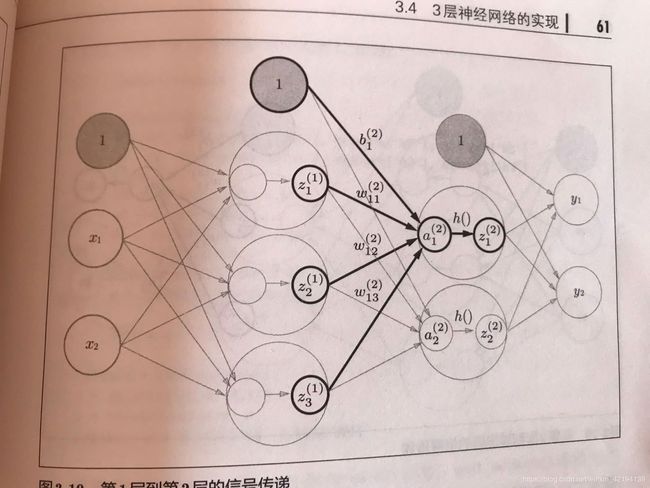
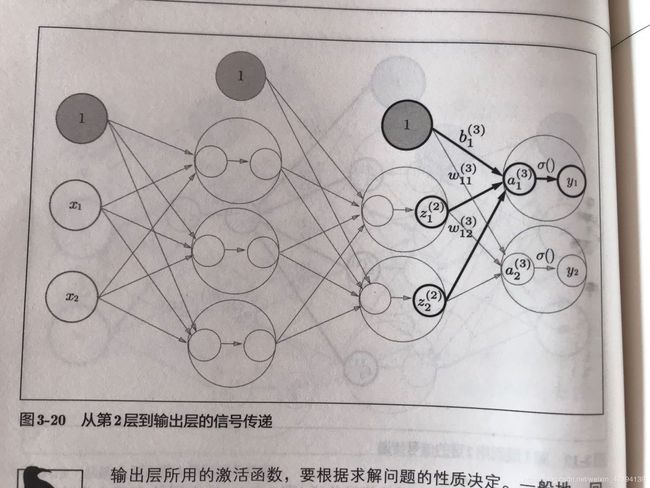
数据在神经网络中流动的示意图为：

这里需要指出一点，激活函数的选择，一般的，回归问题可以使用恒等函数，二分类问题使用sigmoid函数，多分类问题使用softmax函数。

3.4输出层的设计

    神经网络可以用在回归和分类问题上，但是需要根据实际问题修改输出层的激活函数，一般而言，回归问题用恒等函数，输出层使用一个神经元就可以；分类问题用softmax函数，输出层的神经元需要根据分类的总类别进行确定。本小节主要介绍softmax函数。

    假设输出层一共有n个神经元，那么第k个神经元的softmax输出为：。分子是该神经元经过指数函数的值，分母是所有神经元经过指数函数的值的和。softmax函数输出的值在0-1之内，因此可以看作输出“概率”。而且它并不改变原始数据的大小比较，大的原始数据输出大的“概率”值，小的原始数据输出小的“概率”值。

    但是，softmax在计算机的运行时有一定的缺陷，那就是存在溢出的可能，因为神经元的值很大时，经过指数函数计算得到的值会非常非常大，大到计算机无法表示，因此，我们对softmax函数进行如下改造：

    上式中的c‘一般取输出层神经元的最大值的负值，通过减掉该最大值来避免溢出问题，实现代码如下：

import numpy as np

a=np.array([1,2,3])#假设输出层有三个神经元，值分别是1，2，3

def softmax(a):
    a_max=np.max(a)
    e_a=np.exp(a-a_max)
    e_sum=np.sum(e_a)
    y=e_a/e_sum

    return y

    假设我们现在已经训练好了神经网络模型，打算用这个模型来进行识别手写mnist数据，代码如下：

    首先展示引入的库和定义的函数：

import numpy as np
import sys, os
sys.path.append(os.pardir)#将当前目录的父目录添加到搜索目录中以便能够加载load_mnist函数
                          #因为load_mnist函数不在当前目录，在当前目录的父目录中

from dataset.mnist import load_mnist


def get_data():
    (x_train,t_train),(x_test,t_test)=\
    load_mnist(normalize=True,flatten=Trun,one_hot_label=False)
    
    return x_test,t_test

def init_network():
    with open("sample_weight.pkl",'rb') as f:  #训练好的权重和偏置保存在sample_weight文件中
        network=pickle.load(f)
    
    return network

def predict(network,x):
    W1,W2,W3=network['W1'],network['W2'],network['W3']    
    b1,b2,b3=network['b1'],network['b2'],network['b3']

    a1=np.dot(x,W1)+b1
    z1=sigmoid(a1)
    a2=np.dot(z1,W2)+b2
    z2=sigmoid(a2)
    a3=np.dot(z2,W3)+b3
    y=np.softmax(a3)

    return y

    进行测试处理：

x,t=get_data()
network=init_network()

accuracy_cnt=0
for i in range(len(x)):
    y=predict(network,x)
    p=np.argmax(y)#得到概率最高的元素的索引
    if p==t[i]:
        accuracy_cnt+=1
    
print("accuracy:"+str(float(accuracy_cnt)/len(x)))

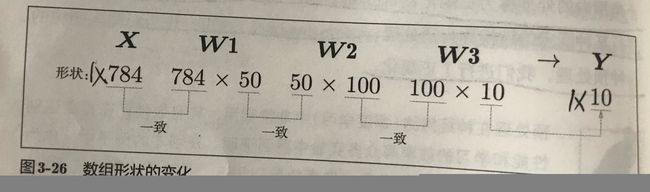
    可以看到，上面的代码在预测图像时，是一幅一幅的进行的，示意图如下：

    那么，可不可以多幅图像一起处理呢？答案是肯定的，多幅图像一起处理叫做批处理，示意图和代码如下：

x,t=get_data()
network=init_network()

batch_size=100#批处理的大小
accuracy_cnt=0

for i in range(0,len(x),batch_size):
    x_batch=x[i:i+batch_size]
    y_batch=predict(network,x_batch)
    p=np.argmax(y_batch,axis=1)#axis=1表示从每行中挑选概率最大的元素，=0表示列
    accuracy_cnt+=np.sum(p==t[i:i+batch_size])

print("accuracy:"+str(float(accuracy_cnt/len(x))))