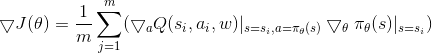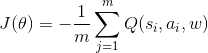深度强化学习9——Deep Deterministic Policy Gradient（DDPG）
从名字上看DDPG是由D(Deep)+D(Deterministic)+PG(Policy Gradient)组成，我们在深度强化学习7——策略梯度（Policy Gradient）已经讲过PG，下面我们将要了解确定性策略梯度(Deterministic Policy Gradient，简称DPG)。
Deterministic Policy Gradient（DPG）
为什么需要确定性策略梯度？主要是因为PG有以下缺点：
- 即使通过PG学习得到了随机策略之后，在每一步行为时，我们还需要对得到的最优策略概率分布进行采样，才能获得action的具体值，而action通常是高维的向量，比如25维、50维，在高维的action空间的频繁采样，无疑是很耗费计算能力。
- 计算梯度需要通过蒙特卡洛采样来进行估算，需要在高维的action空间进行采样，耗费计算能力。
简单来说，对于某一些动作集合来说，它可能是连续值，或者非常高维的离散值，这样动作的空间维度极大。如果我们使用随机策略，即像DQN一样研究它所有的可能动作的概率，并计算各个可能的动作的价值的话，那需要的样本量是非常大才可行的。
所以在2014年，由Deepmind的D.Silver等提出：Deterministic policy gradient algorithms，即作为确定性策略，相同的策略，在同一个状态处，动作是唯一确定的
在这之前，业界普遍认为，环境模型无关(model-free)的确定性策略是不存在的，而D.Silver等通过严密的数学推导，证明了DPG的存在。我们回顾一下策略梯度，基于Q值的梯度计算公式：
![\bigtriangledown _{\theta }J(\pi_{\theta})=E_{s\sim p^{\pi},a\sim \pi_{\theta}}[\bigtriangledown _{\theta }log\pi_{\theta}(a|s)Q^{\pi}(s,a)]](http://img.e-com-net.com/image/info8/8d63cc94448d46ce80159fd84cafe677.gif){kind=small}
随机性策略梯度需要在整个动作空间
采样，而DPG梯度公式如下：
![\bigtriangledown _{\theta }J(\mu_{\theta})=E_{s\sim p^{\mu}}[\bigtriangledown _{\theta }\mu_{\theta}(s)\bigtriangledown _{a}Q^{\mu}(s,a)|_{a=\mu_{\theta}}]](http://img.e-com-net.com/image/info8/9886a4d59c3f4716ad483a9617ee096c.gif){kind=small}
跟随机策略梯度的式子相比，对动作的积分变为回报Q函数对动作的导数。
Deep Deterministic Policy Gradient （DDPG）
Deepmind在2016年提出DDPG，将深度学习神经网络融合进DPG的策略学习方法。 相对于DPG的核心改进是：采用卷积神经网络作为策略网络和Q网络，与前面介绍的方法不同的是DDPG有四个网络。
DDPG采用确定性策略
来选取动作，其中
产生确定性动作的策略网络的参数，根据前面我们讲过的AC算法，可以联想到使用策略网络充当Actor，使用价值网络充当Critic，再根据上述DPG算法，Actor部分不再使用自己的Loss函数和Reward进行更新，而是使用critic部分Q值对action的梯度来对actor进行更新。
事实上如果我们只用当前价值网络评估Q值，会产生过估计，我们回顾深度强化学习6——DQN的改进方法中的Double DQN(DDQN)，先在当前Q网络中先找出最大Q值对应的动作，在目标网络里面去计算目标Q值，我们能不能采用类似的方法去估计Q值？回到DDPG，critic部分增加一个目标网络与DDQN的目标Q网络功能类似，但是还需要选取动作用来估计目标Q值，由于我们有自己的Actor策略网络，用类似的做法，增加一个Actor目标网络，对经验回放池中采样的下一状态使用贪婪法选择动作。
根据上面的思路，我们也得到了DDPG的四个网络，来总结一下：
- Actor当前网络：负责策略网络参数
的迭代更新，负责根据当前状态S选择当前动作A，用于和环境交互生成S', R - Actor目标网络：负责根据经验回放池中采样的下一状态 S' 选择最优下一动作 A'，网络参数
定期从复制 - Critic当前网络：根据目标Q值对网络参数 w 进行迭代更新，负责计算当前Q值，其中目标Q值
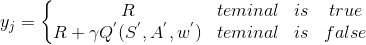
- Critic目标网络：负责计算目标Q值中的
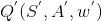，网络参数 w' 定期从 w 复制
此外，DDPG从当前网络到目标网络的复制和我们之前讲到了DQN不一样。回想DQN，我们是直接把将当前Q网络的参数复制到目标Q网络， DDPG这里没有使用这种硬更新，而是使用了软更新，即每次参数只更新一点点
其中
是更新系数，同时，为了学习过程可以增加一些随机性，探索潜在的更优策略，通过Ornstein-Uhlenbeck process（OU过程）为action添加噪声，最终输出的动作A为
最后对于 Actor当前网络，这里由于是确定性策略，原论文定义的损失梯度为
假如对同一个状态，我们输出了两个不同的动作
和
，从Critic当前网络得到了两个反馈的Q值，分别是
，假设
，即采取动作可以得到更多的奖励，那么策略梯度的思想是什么呢，就是增加的概率，降低的概率，也就是说，Actor想要尽可能的得到更大的Q值。所以我们的Actor的损失可以简单的理解为得到的反馈Q值越大损失越小，得到的反馈Q值越小损失越大，因此只要对状态估计网络返回的Q值取个负号即可，即：
DDPG可以看做是DDQN、Actor-Critic和DPG三种方法的组合算法，完整的算法流程如下
总结
DDPG参考了DDQN的算法思想，通过双网络和加一些其他的优化，比较好的解决了Actor-Critic难收敛的问题，实际上DDPG也在一些产品中得到了应用。针对策略梯度还有一个优化算法PPO，PPO算法本质上是一个AC算法，有Actor和Critic神经网络，详细讲解可以参考李宏毅—PPO。
DDPG算法github demo地址：https://github.com/demomagic/DDPG.git
PS： 如果觉得本篇本章对您有所帮助，欢迎关注、评论、赞！如果要转发请注明作者和出处
参考文献：
[1] 强化学习(十六) 深度确定性策略梯度(DDPG)