工作总结2019-

---

S

有时pip很慢，因为是国外的网站，就用清华镜像
pip install pip -U  # 升级到最新的版本
pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple    # 配置pip从清华下载

python包的更新
pip install --upgrade xxx(==版本号)

各python包下载链接
https://www.lfd.uci.edu/~gohlke/pythonlibs/
或pypi

---

直接把时间串转为时间格式
from dateutil.parser import parse
a='202002020820'
b=parse(a)
print(b)
# datetime.datetime(2020, 2, 2, 8, 20)

把时间格式转为str
import datetime as dt
c=dt.datetime.strftime(b,'%Y%m%d%H%M%S')
# '20200202082000'

np.reshape[-1] 可以先把三维数组变成1维对数据做处理 再reshape回原维度
不管reshape什么样的数据，顺序一直不会变

round(a,1) # 保留一位小数

多维数据归一化保留几位小数
simg=np.around(img/255,decimals=3)  # 保留3位小数
simg=(img/255.).astype(np.float32) # 正确的图片归一化

如果图片归一化很卡，图像分辨率大，归一化后小数更占内存
不想做归一化可以再CNN第一层加个BN，即便归一化后加BN也能加快收敛

str(a).zfile(2) # 字符串补全到2位，比如a=1，结果为01

arr.T 等同于 np.transpose(arr)

np.set_printoptions(suppress=True) # numpy非科学计数显示

c=np.hstack((a,b)) 横向拼接，等同于column_stack
c=np.vstack((a,b)) 纵向拼接

b.sort(key=lambda x:x[-18:-4]) 自定义排序，以lambda里面的来排

data = np.delete(np.array(table),-1,axis=1) # 数据集去掉最后一列

pr = [((i if i > 0 else 0) if i<2000 else 2000) for i in pr] # 吧大于1w的为1w，小于0的为0

random.shuffle(datas) # 打乱样本集，防止数据分布对模型结果的影响（批量训练过拟合）

dataset = np.where((dataset == missValue), 2323, dataset) # 无效值替换为2323
z=np.where(dataset==2323) # 得到下标的列表

list.reverse()  # 列表反转，没有返回值
reversed(list)  # 返回反转的list

替换列表中值的一种写法
data=np.array([[3,4],[5,6],[7,8]])
data[:,1][data[:,1]==6]=65535
print(data)
a=[2,3,5,6]
a[a==2]=23
print(a)  # [23,3,5,6]

由于在Python2 中的默认编码为ASCII，但是在Python3中的默认编码为UTF-8。
所以在使用np.load(det.npy)的时候会出现错误提示：
you may need to pass the encoding= option to numpy.load
当遇到这种情况的时候，用np.load(det.npy,encoding=“latin1”)就可以了

table=pd.read_csv(‘data.csv’).fillna(method=‘bfill’)
# 空值填充，pad / ffill是用前面行/列的值填充， backfill / bfill表示用后面行/列的值填充

os.path.sep # 目录分隔符
os.path.splitext(a) # 切分后缀
os.path.splitext(a) # 切分目录和文件

# 二维数组，数据都从str变成float
res = [list(map(float, i)) for i in res]  
res = np.array(res)
# 二维数组，数据（温度）都-273.1
res = [list(map(lambda x: x - 273.1, i)) for i in res]  

files = glob.glob(r"/COM/data/*.soi") # 返回所有匹配的文件路径+文件名列表，加上r让字符串不转义

对2D数组画图
from pylab import *
data[data<0]=NAN  # 为NAN画出来的是透明的
imshow(data)  # 直接画出带颜色的，用contourf(data)也可以，这个更高级、自动插值
imsave('1.png',data)
show()   
然后可以用opencv读取，此时变成了三个通道带颜色的数组，继续做后续处理

M

print(1) 等同于 sys.stdout.write(1)
# 把打印重定向文件
f=open('outfile.log',"a+") 
sys.stdout=f   # 之后的print都输入到了文件里
print('in outfile')

import os
print(os.getpid())  # 获取本程序进程id
print(os.kill(os.getpid(), 9))  # kill -9 pid，可能等同于exit()
print(111)

# 锁可以使程序同步，不会发生脏读误读
import threading
lock = threading.Lock()
lock.acquire()  # 获得锁标记
lock.release()  # 释放锁

查看CPU、GPU

import os
from tensorflow.python.client import device_lib
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "99"
print(device_lib.list_local_devices())

traceback异常

import traceback  
try:
    a=0/0
except Exception as e:
    print('err ',e)  # division by zero
    traceback.print_exc()  # 红字打印错误，但程序继续运行
    print(traceback.format_exc())  # 白字打印错误，可定向到log
    print(1)

psutil系统监控

import psutil  #  监测文件系统的变化
# 获得系统的CPU、内存、磁盘使用率
cpu = psutil.cpu_percent(3)
mem = psutil.virtual_memory().percent
disc = psutil.disk_usage('E:/').percent

hashlib加密

# 数据加密，常用来做暗文判断，防盗
import hashlib
md5 = hashlib.md5('23'.encode('utf-8'))  # 括号里可加可不加，加入字符串使解密更复杂
md5.update("1".encode('utf-8'))
print(md5.hexdigest())
# md5是128 bit字节，sha1是160 bit字节，一个字符是4字节
sha1=hashlib.sha1()
sha1.update("1".encode('utf-8'))
print(sha1.hexdigest())

psycopg2连接DB

# 连接postgre数据库
import psycopg2 as pg
def doDB(sql):
    conn = pg.connect(database="satview_app", user="postgres", password="postgres", host="172.10.10.10",
                      port="5432")
    cur = conn.cursor()
    cur.execute(sql)
    conn.commit()
    cur.close()
    conn.close()
    
# 一次性多条插入
sql = "insert into acmr values "
for i in datas:  
    sql += "('%s','%s',%s,%s,%s,%s)," % tuple(i)
sql = sql[:-1]
doDB(sql)

# 从数据库获取数据
conn=pg.connect(database="satview_app", user="postgres", password="postgres", host="172.10.10.10", port="5432")
cur=conn.cursor()
cur.execute("select * from acmr  ")
res=cur.fetchall()  # 或fetchone()
cur.close()
conn.close()

获取数据库中最近得时间
SELECT curtime from zr_wind ORDER BY curtime desc LIMIT 1
和新数据作比较做操作

postgre数据库字段顺序是tuple存储，顺序不能变，不像mysql
PostgreSQL的物理存储，在PG中，数据是tuple组织的，每个tuple都是固定的storage layout，即字段存储的物理顺序是固定的

解析不同格式文件

解析grib数据，.grb
可以在linux上用pygrib解，可以用wgrib解，也可以用gdal解

import gdal
import numpy as np

fn='11f16.grb'
ds=gdal.Open(fn)
print(ds)
print(ds.GetDescription())#数据描述

cols = ds.RasterXSize#列数
rows = ds.RasterYSize#行数
bands = ds.RasterCount#波段数
print(cols,rows,bands)
print(gdal.Info(ds))  # 数据各波段详细信息

data = np.zeros((bands, rows, cols), dtype=np.float64)#存放数据的数组
for i in range(bands):
    data[i] = ds.GetRasterBand(i + 1).ReadAsArray(0, 0, cols, rows)#逐波段读数据

print(data.shape)  # bands,rows,cols

# 解析dat
f = open('xxx.dat', "rb+")
data = f.read()
d1 = struct.unpack('24775200f', data)  # 24775200=len(data)/4，二进制转化为浮点数
print(len(d1),type(d1),type(d1[1]))  # 24775200 , tuple , float
d1=np.array(d1)
odata = d1.reshape((62, 555,720))   # 24775200 = 555*720*62

# 读取nc
from netCDF4 import Dataset
ncfile=Dataset('Radar48.nc')
keys =list( ncfile.variables.keys() )
attvalue = ncfile.variables[keys[0]]

# 读取Excel
import xlrd   
# 加载Excel
xlsbook = xlrd.open_workbook(xlsfile)
# 打开Sheet1
location = xlsbook.sheet_by_name(u'Sheet1')
# 取得第一和第二列全部的值
lon = location.col_values(0,0,location.nrows)
lat = location.col_values(1,0,location.nrows)
num = location.col_values(2,0,location.nrows)

# 解析xml
from xml.dom.minidom import parse
def parses(xmlfile):     
    x=parse(xmlfile)
    root=x.documentElement
    a=root.getElementsByTagName('JobCmdLine')
    for i in range(len(a)):
        t=a[i].getAttribute('Value')

# 读写csv
# 写
import csv
with open('data.csv', 'w', newline='') as csv_file:
    csv_writer = csv.writer(csv_file)
    csv_writer.writerow(['year','mon','day','xxx'])
    for data in datas:
        csv_writer.writerow(data)
        
# 读
import pandas as pd
table = pd.read_csv('datavis.csv')
data = np.array(table)
print(table.columns)  # 表头

读取hdf
import h5py
f=h5py.File('E:\Surface.hdf','r')
print(f)
print(f.keys())
a=list(f.keys())  # 每个通道
for i in a:
    print(i)
    data=list(f[i])
    print(len(data))
    data=np.array(data)
    print(data.shape)   

写HDF
import h5py
output_file='pressure.hdf'
f = h5py.File(output_file, 'w')
f.create_dataset('ele1', data=data1, dtype=data1.dtype) # data1是一个numpy数组
f.create_dataset('ele2', data=data2, dtype=data2.dtype)
f[dataset].attrs['ele2'] = np.array([40,4,4])  # # 添加属性
f.close()

SQL

insert into xx values (1,‘23’,‘xxx’) on conflict(id,username) do update set data=‘b’
通过id+uname联合约束，不重复(没有)就添加，有了就更新

L

线程

在UNIX平台上，当某个进程终结之后，该进程需要被其父进程调用wait，否则进程成为僵尸进程(Zombie)。所以，有必要对每个Process对象调用join()方法 (实际上等同于wait)。对于多线程来说，由于只有一个进程，所以不存在此必要性。
multiprocessing提供了threading包中没有的IPC(比如Pipe和Queue)，效率上更高。

我们可以从下面的程序中看到Thread对象和Process对象在使用上的相似性与结果上的不同。各个线程和进
程都做一件事：打印PID。但问题是，所有的任务在打印的时候都会向同一个标准输出(stdout)输出。这样输出的字符会混合在一起，无法阅读。使用Lock同步，在一个任务输出完成之后，再允许另一个任务输出，可以避免多个任务同时向终端输出

import os
import threading
import multiprocessing

# Main
print('Main:', os.getpid())

# worker function
def worker(sign, lock):
    lock.acquire()
    print(sign, os.getpid())
    lock.release()

# Multi-thread
record = []
lock = threading.Lock()

# Multi-process
record = []
lock = multiprocessing.Lock()

if __name__ == '__main__':
    for i in range(5):
        thread = threading.Thread(target=worker, args=('thread', lock))
        thread.start()
        record.append(thread)

    for thread in record:
        thread.join()
    
    for i in range(5):
        process = multiprocessing.Process(target=worker, args=('process', lock))
        process.start()
        record.append(process)
    
    for process in record:
        process.join()

画图

可能有些运行不了，只是记录pylab画各种图的方法

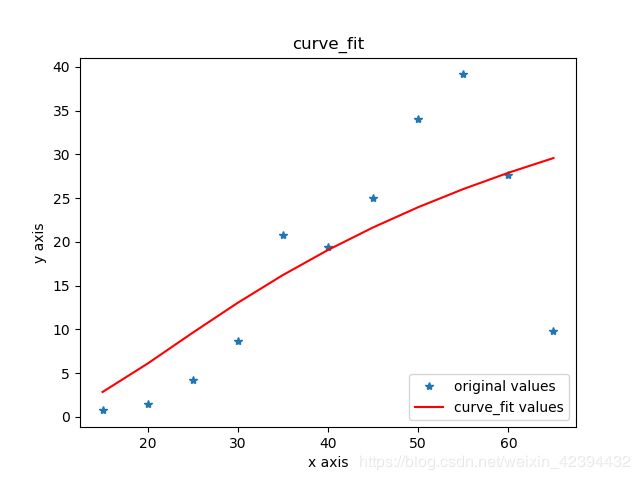
曲线拟合

import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import numpy as np
x = np.arange(15, 66, 5)
print(x,type(x))
y = np.array([0.751694694, 1.510593775
, 4.207583892, 8.670868118, 20.7398795
, 19.37581188, 25.0455539, 34.07165373
, 39.12968784, 27.60011882, 9.815811524])
def func(x,a,b):
    return a*np.exp(b/x)
popt, pcov = curve_fit(func, x, y)
a=popt[0]#popt里面是拟合系数，读者可以自己help其用法
b=popt[1]
yvals=func(x,a,b)
plot1=plt.plot(x, y, '*',label='original values')
plot2=plt.plot(x, yvals, 'r',label='curve_fit values')
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.legend(loc=4)#指定legend的位置,读者可以自己help它的用法
plt.title('curve_fit')
plt.show()
plt.savefig('p2.png')

多项式拟合

import matplotlib.pyplot as plt
import numpy as np
x = np.arange(10, 61, 5)
y = np.array([0.227769477338322,
0.283520351840111,
0.468174341740669,
1.04241943278196,
3.16516445953794,
12.2406974733659,
8.49918202494270,
10.8766298540945,
14.1689240413731,
19.9027296869527,
19.2269581524847])
z1 = np.polyfit(x, y, 3)#用3次多项式拟合
p1 = np.poly1d(z1)
print(p1) #在屏幕上打印拟合多项式
yvals=p1(x)#也可以使用yvals=np.polyval(z1,x)
plot1=plt.plot(x, y, '*',label='original values')
plot2=plt.plot(x, yvals, 'r',label='polyfit values')
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.legend(loc=4)
plt.title('polyfitting')  # 多项式拟合
plt.show()

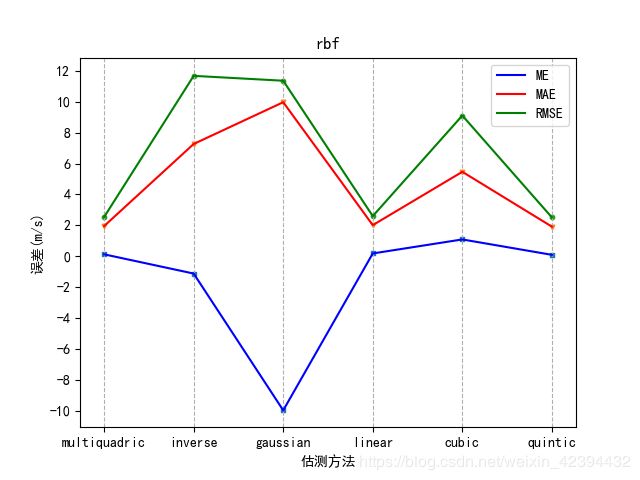
插值误差分析画图

import matplotlib.pyplot as plt
def handle(a,b):
    me,mae,rmse,rmsse,rs=[],[],[],[],[]
    for i in a[:,1]:
        # print(len(i))
        me.append(ME(i,data))
        mae.append(MAE(i,data))
        rmse.append(RMSE(i,data))
        rmsse.append(RMSSE(i,data))
        rs.append(Rsqrt(i,data))
    print(len(me),len(mae),len(rmse),len(rmsse),len(rs))

    x = a[:, 0]        # 数据说明，比如D=  func=
    y=[i*2 for i in range(-10,10)]    # y轴标注范围   参照误差的量级做修改

    plt.figure()
    plt.title(b)
    plt.grid(axis='x',linestyle='--')
    plt.scatter(x,me,s=10,marker='s')
    plt.scatter(x,mae,s=10,marker='v')
    plt.scatter(x,rmse,s=10,marker='o')
    # plt.xticks(x)
    plt.xticks([i for i in range(10)])    #  x轴标准
    plt.yticks(y)
    plt.xlabel('估测方法')           # x轴说明
    plt.ylabel('误差(m/s)')
    plt.plot(x,me,color='b',label='ME')
    plt.plot(x,mae,color='r',label='MAE')
    plt.plot(x,rmse,color='g',label='RMSE')
    plt.legend()   # loc=
    plt.show()

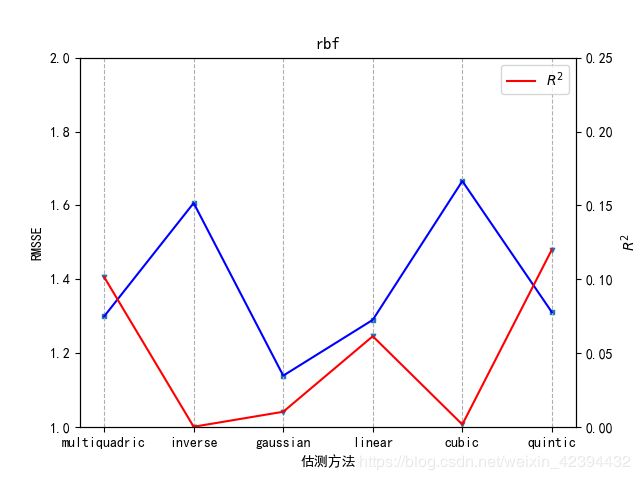
    #   关于RMSSE和R的图

    # from mpl_toolkits.axes_grid1 import host_subplot
    # import mpl_toolkits.axisartist as AA
    # host=host_subplot(111,axes_class=AA.Axes)
    # plt.subplots_adjust(right=0.75)
    # host=plt.subplot(111)
    # p1=plt.twinx()
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ax.set_title(b)
    ax.plot(x, rmsse, color='b', label='RMSSE')
    ax2=ax.twinx()
    ax2.plot(x, rs, color='r', label='$R^2$')
    ax.grid(axis='x',linestyle='--')
    ax.set_xlabel('估测方法')
    # ax.set_xticks(i for i in range(10))
    ax.set_ylabel('RMSSE')
    ax2.set_ylabel('$R^2$')
    ax.scatter(x, rmsse, s=10, marker='s')
    ax2.scatter(x, rs, s=10, marker='v')
    # yy = [i * 0.2 for i in range(0, 10)]  # y轴标注范围
    # yyy = [i * 0.05 for i in range(0, 5)]  # y轴标注范围
    # ax.set_ylim(0.5,1.5)
    ax.set_ylim(1,2)  # for rbf
    # ax.set_xlim(3,22)
    ax2.set_ylim(0,0.25)
    plt.legend(loc='best')
    plt.show()

handle(rbf,'rbf')

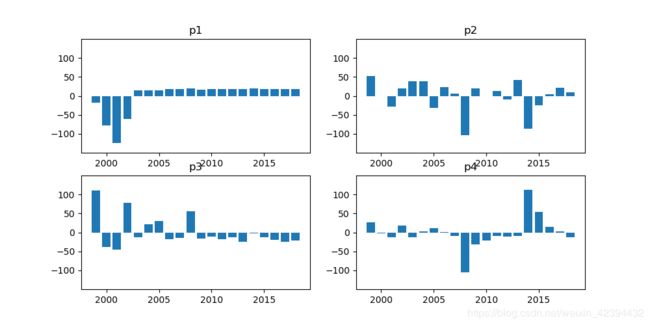
EOF分析画图

from pylab import *
p1=np.load('E:\EOFsss\p1.npy')
p2=np.load('E:\EOFsss\p2.npy')
p3=np.load('E:\EOFsss\p3.npy')
p4=np.load('E:\EOFsss\p4.npy')

# xticks(range(1999,2019,4))
# yticks(range(-100,100,50))

figure(1,figsize=(10,5))
ax=subplot(2,2,1)
sca(ax)
title('p1')
# xticks(range(1999,2019,4))
yticks(range(-100,101,50))
ylim(-150,150)
bar(range(1999,2019,1),p1*40)
ax1=subplot(2,2,2)
sca(ax1)
title('p2')
# xticks(range(1999,2019,4))
yticks(range(-100,101,50))
ylim(-150,150)
bar(range(1999,2019,1),p2*40)
ax2=subplot(2,2,3)
sca(ax2)
title('p3')
# xticks(range(1999,2019,4))
yticks(range(-100,101,50))
ylim(-150,150)
bar(range(1999,2019,1),p3*40)
ax3=subplot(2,2,4)
sca(ax3)
title('p4')
# xticks(range(1999,2019,3))
yticks(range(-100,101,50))
ylim(-150,150)
bar(range(1999,2019,1),p4*40)

show()

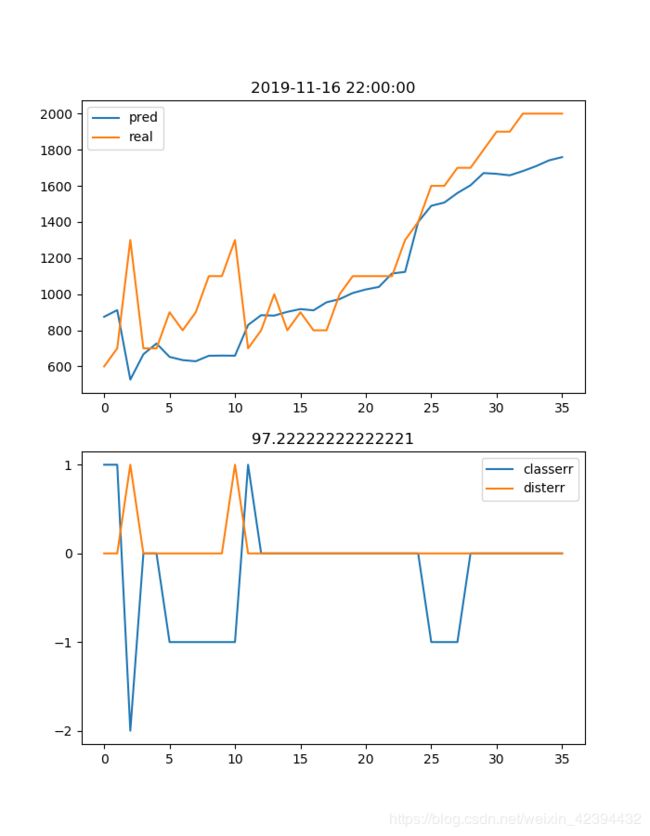
AI预测结果画图

from pylab import *
figure(figsize=(7, 9))
subplot(2, 1, 1)
title(timec[t])
# yticks([i for i in range(0,10001,500)])
# ylim([0,10001])
plot(xx, pr, label='pred')
plot(xx, yr, label='real')
legend()

subplot(2, 1, 2)
K = classerr.count(-1)  / OutputSize * 100
title(K)
yticks([i for i in range(-10, 10, 1)])
plot(xx, classerr, label='classerr')
plot(xx, disterr, label='disterr')
legend()
print('K = ', K)
show()

本人出的面试题

1、用python实现计算特征X和Y之间的相关系数的方法

2、写一个方法：求列表主元素，对应元素个数大于列表长度的一半即为主元素，没有则为None
Eg：[1,1,1,2,2,2,2],输出2

3、实现一个自定义排序
比如：a=[ ‘z_RES23’,‘p_RES93’,‘x_RES21’,‘z_RES23’,‘d_RES04’,‘z_RES13’ ]
通过最后两位从小到大排序

4、写一个快速排序

5、写一个二分查找

6、一行代码实现1-100之和

7、假设你在卷积神经网络的第一层中有 5 个卷积核，每个卷积核尺寸为 7×7，具有零填充且步幅为 1。该层的输入图片的维度是 224×224×3。那么该层输出的维度是多少？

8、向量 X=[1,2,3,4,-9,0] 的 L1 、L2范数为

9、过拟合和欠拟合的解决方法

10、机器学习训练时，Mini-Batch 的大小优选为2的幂，如 256 或 512。它背后的原因是什么？

答案

python

1、
用python实现 计算特征 X 和 Y 之间的相关系数的方法

def R(x, y):
    xm = np.mean(x)
    ym = np.mean(y)
    mem = sum((x - xm) * (y - ym))
    den = np.sqrt( sum((x - xm) ** 2) * sum((y - ym) ** 2) )
    return mem / den

#2、
求列表 l1 和 l2 的差集

list(set(l1).difference(set(l2)))

3、
写一个方法：求列表主元素，对应元素个数大于列表长度的一半即为主元素，没有则为None
Eg：[1,1,1,2,2,2,2],输出2

def main():    
    a=[1,1,1,2,2,2,2]
    for i in set(a):
        if a.count(i)>len(a)/2:
               return i
    return None

4、
20个人围成一圈（编号1-20），从1开始依次报数，以7为一个循环，报数为3的倍数退出，问最后剩哪两人

human=[i for i in range(1，21)]
human1=human.copy()
con=1
while len(human)!=2:
        for i in human:
                if con%3==0:human1.remove(i)
                con+=1
                if con==8:con=1
        human=human1.copy()
        print(human)
print('last = ',human)
# 结果，【13，15】

5、
对一个列表位置反转，a=[1,2,3,4,5,6,4]

a[::-1] 或 a.reverse()

6*、
实现一个自定义排序
比如：a=[ ‘z_RES23’,‘p_RES93’,‘x_RES21’,‘z_RES23’,‘d_RES04’,‘z_RES13’ ]
通过最后两位从小到大排序

b.sort(key=lambda x:x[-2:])

#7、
10个台阶，小明每次只能上1个或2个台阶，一共有多少种走法

动态规划
def do(n):  
        if n==2:return 2
        elif n==1:return 1
        else:return do(n-1)+do(n-2)
print(do(10))

8、
写一个快速排序

qs=lambda a:( (qs([i for i in a[1:] if i<=a[0]]))+[a[0]]+(qs([i for i in a[1:] if i > a[0]])) ) if len(a)>1 else a
（如果分解的只剩一个元素，就输出，从小到大的list拼接）
a=[3,5,7,9,2]
print(qs(a))

9、
写一个二分查找

def query(key,l,beg,end): 
    if beg>=end:
        return
    mid=int((beg+end)/2)
    if l[mid]>key:
        return query(key,l,beg,mid)
    elif l[mid]<key:
        return query(key,l,mid,end)
    else:
        return mid
result=query(key,l,0,len(l)-1)

时间复杂度O(logn)

或

int binarySearch(int l,int r,int number) //循环{    
	int mid = (l+r)/2;     
	while(l<=r){         
		if(t[mid]<number)                
			l = mid+1;        
		else if(t[mid]>number)            
			r = mid-1;        
		else  if(t[mid] == number )             
			return mid;           
		mid = (r+l)/2;    }    
	return -1;

10*、
实现斐波那契数列

用生成器yield
def fun(z):
    x1,x2=0,1
    for i in range(z):
        yield x1
        x1,x2=x2,x1+x2
for i in fun(int(input('输入一个数n，你将得到斐波那契数列前n项\n'))):
        print(i,end=' ')

#11、
给定一个字符串，找出不含有重复字符的最长字串的长度

滑动窗口法
def do(s):
    a=0
    d={}
    start=0
    for i in range(len(s)):
        if s[i] in d and start<=d[s[i]]:
            start=d[s[i]]+1
        a=max(i-start+1,a)
        d[s[i]]=i
    return a,s[start:start+a]  # 最长值和串

a,b=do('asddfgh')
print(a,b)

12、
一行代码实现1-100之和

sum(range(1,101))

13*、
最大回文子串，Eg: in ‘abccbac’ out: ‘abccba’

a='abccbac' 

def do(a):
        lens,start=0,0
        for i in range(len(a)):
                if i-lens>=1 and a[i-lens-1:i+1]==a[i-lens-1:i+1][::-1]:
                        start=i-lens-1
                        lens+=2
                        continue
                if i-lens>=0 and a[i-lens:i+1]==a[i-lens:i+1][::-1]:
                        start=i-lens
                        lens+=1
        return start,lens,a[start:start+lens]

print(do(a))

14、
有一个二维数组data，里面的元素全部是数字，但是都是str类型，一行代码全部转成float类型

res = np.array( [list(map(float, i)) for i in res] )

---

AI

1、
BP和CNN的区别

BP每层单元都是全连接的，而CNN他是连接到卷积核
卷积网络其实就是在全连接网络的基础上，把全连接改为部分连接，然后再利用权值共享的技巧大量减少网络需要修改的权值数量

2、
假设你在卷积神经网络的第一层中有 5 个卷积核，每个卷积核尺寸为 7×7，具有零填充且步幅为 1。该层的输入图片的维度是 224×224×3。那么该层输出的维度是多少？

答案：218 x 218 x 5

解析：一般地，如果原始图片尺寸为 nxn，filter 尺寸为 fxf，则卷积后的图片尺寸为 (n-f+1)x(n-f+1)，注意 f 一般为奇数。
若考虑存在填充和步幅，用 s 表示 stride 长度，p 表示 padding 长度，如果原始图片尺寸为 nxn，filter 尺寸为 fxf，则卷积后的图片尺寸为：out=(in+2*p-f)/s+1
此例中， n=224，p=0，f=7，s=1，因此，该层输出的尺寸为 218x218。
输出的第三个维度由滤波器的个数决定，即为 5

3*、
机器学习训练时，Mini-Batch 的大小优选为2个的幂，如 256 或 512。它背后的原因是什么？

Mini-Batch 设为 2 的 幂，是为了符合 CPU、GPU 的内存要求，利于并行化处理

4、
向量 X=[1,2,3,4,-9,0] 的 L1 、L2范数为

19，√111

L0 范数表示向量中所有非零元素的个数；L1 范数指的是向量中各元素的绝对值之和，又称“稀疏矩阵算子”；L2 范数指的是向量中各元素的平方和再求平方根

5、
CNN中池化层的作用

1、pooling是在卷积网络（CNN）中一般在卷积层（conv）之后使用的特征提取层，使用pooling技术将卷积层后得到的小邻域内的特征点整合得到新的特征。一方面防止无用参数增加时间复杂度，一方面增加了特征的整合度。

2、pooling是用更高层的抽象表示图像特征，至于pooling为什么可以这样做，是因为：我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，为了描述大的图像，一个很自然的想法就是对不同位置的特征进行聚合统计。这个均值或者最大值就是一种聚合统计的方法。

3、做窗口滑动卷积的时候，卷积值就代表了整个窗口的特征。因为滑动的窗口间有大量重叠区域，出来的卷积值有冗余，进行最大pooling或者平均pooling就是减少冗余。减少冗余的同时，pooling也丢掉了局部位置信息，所以局部有微小形变，结果也是一样的。就像图片上的字母A，局部出现微小变化，也能够被识别成A。而加上椒盐噪音，就是字母A上有很多小洞，同样的能够被识别出来。而平移不变性，就是一个特征，无论出现在图片的那个位置，都会识别出来。所以平移不变性不是pooling带来的，而是层层的权重共享带来的

6*、
对于分类问题常用的评价指标是精准度、召回率、F1值，他们的定义

TP——将正类预测为正类数
FN——将正类预测为负类数
FP——将负类预测为正类数
TN——将负类预测为负类数

精准率定义为：P = TP / (TP + FP)
召回率定义为：R = TP / (TP + FN)
F1值定义为： F1 = 2PR / (P + R)

7、
讲讲激活函数sigmoid、tanh、relu、softmax

sigmoid(1/1+e-z，一般用在简单二分类输出层)
tanh(ez-e-z/ez+e-z，一般用在隐藏单元，tanh的输出为(-1,1)，因此它将数据集中在一起，使得下一层的学习变得更加简单，一般用在RNN)
relu(x>0:x，常用在模型训练层)
leaky ReLU(x<0:0.01x)
softmax（z/sum(z)，一般用于CNN输出层）

如果用sigmoid就是二分分类问题，如果用softmax就是多分类，如果用tanh的话常常是RNN，CNN常用relu（非负时梯度恒为1，收敛维持稳定，如果用leaky带泄露的，就是负数时梯度不为0，可以防止梯度消失）

8、过拟合和欠拟合的解决方法

降低过拟合方法
数据扩充（图像变换.Gan生成.MT生成等）
降低模型复杂度（神经网络减少层数.神经元个数.决策树剪枝等）
权值约束（L1L2等）
集成学习（dropout、RF、GBDT等）
提前终止

降低欠拟合方法
加入新特征（因子分解机FM、Deep-Crossing、自编码器）
增加模型复杂度（神经网络增加层数.神经元个数）
减少或去掉正则化（添加正则化项是为了限制模型的学习能力，减小正则化项的系数则可以放宽这个限制；模型通常更倾向于更大的权重，更大的权重可以使模型更好的拟合数据）

9、
讲讲PCA

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。
PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。
通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理

10、
讲一个你最常用的机器学习算法，定义、特点、优缺点、应用场景等

（开放，不看对错）

11、
简述LSTM

LSTM(Long Short-Term Memory)是长短期记忆网络，是一种时间递归神经网络，适合于处理和预测时间序列中间隔和延迟相对较长的重要事件。

LSTM 已经在科技领域有了多种应用。基于 LSTM 的系统可以学习翻译语言、控制机器人、图像分析、文档摘要、语音识别图像识别、手写识别、控制聊天机器人、预测疾病、点击率和股票、合成音乐等等任务。

LSTM区别于RNN的地方，主要就在于它在算法中加入了一个判断信息有用与否的"处理器"，这个处理器作用的结构被称为cell。

一个cell当中被放置了三扇门，分别叫做输入门、遗忘门和输出门。一个信息进入LSTM的网络当中，可以根据规则来判断是否有用。只有符合算法认证的信息才会留下，不符的信息则通过遗忘门被遗忘。

目前已经证明，LSTM是解决长序依赖问题的有效技术，并且这种技术的普适性非常高，导致带来的可能性变化非常多。各研究者根据LSTM纷纷提出了自己的变量版本，这就让LSTM可以处理千变万化的垂直问题。