Numpy生成随机分布函数“二项分布”+“正态分布”，使用matplotlib展示概率质量函数（PMF）／概率密度函数（PDF）

• numpy.random.binomial(n,p,size)：产生size个符合（n，p）的二项分布随机数

即，相当于进行size次实验，每次实验都投掷n枚硬币／每次实验都将一枚硬币投掷n次，记录size次实验中，正面朝上分别为0-n次的实验次数；其中每次试验的成功概率为p

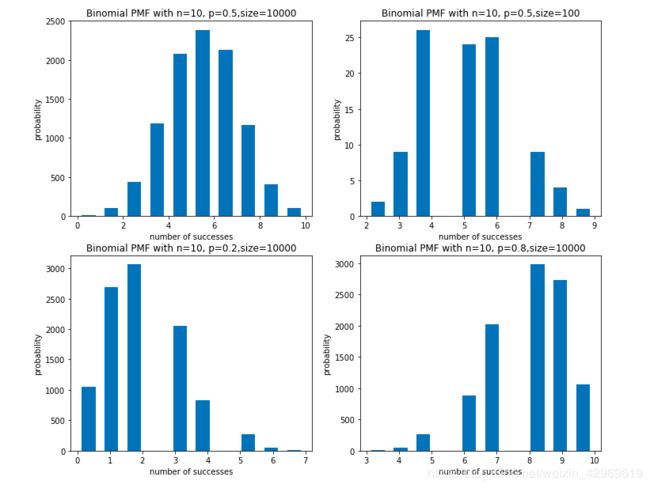
1. 固定n值，对比p和size不同值的不同结果

'''绘制二项分布的概率质量函数，使用不同参数展示'''
import matplotlib.pyplot as ply
import numpy as np

 # 产生二项分布的随机数并制作成直方图
def plot_binomial(n,p,size):
    sample = np.random.binomial(n,p,size)  
    # 绘制直方图，设置标题和坐标
    n,edgebin,patch=plt.hist(sample, bins=n, rwidth=0.6) 
    plt.title('Binomial PMF with n={}, p={},size={}'.format(n,p,size))  
    plt.xlabel('number of successes')
    plt.ylabel('probability')
    # 打印n和bins的取值范围
	print("edgebin = {}".format(edgebin))
    print("size number in bins = {}".format(n))

 # 制作四组不同参数输入的结果图对比
def difference_p_and_size():
    plt.figure(figsize=(12,10))
    
    ax=plt.subplot(221)
    plot_binomial(10, 0.5,10000)
    
    ax=plt.subplot(222)
    plot_binomial(10, 0.5,100)
    
    ax=plt.subplot(223)
    plot_binomial(10, 0.2,10000)
    
    ax=plt.subplot(224)
    plot_binomial(10, 0.8,10000)
    
    plt.show()

# 调用函数    
difference_p_and_size() 

----------------
# 图221中打印的结果：
edgebin = [ 0.  1.  2.  3.  4.  5.  6.  7.  8.  9. 10.]
size number in bins = [  10.  112.  408. 1175. 2062. 2478. 1986. 1200.  443.  126.]

# 图222中打印的结果：
edgebin = [0.  0.9 1.8 2.7 3.6 4.5 5.4 6.3 7.2 8.1 9. ]
size number in bins = [ 1.  4.  6. 16. 17. 27. 16.  7.  5.  1.]

说明：

（1）每组“size number in bins”之和 = “size”参数；
bins的取值范围在0-n之间，但是根据随机数生成的结果不一样，bins的取值会不同
（2）对于二项分布来说，size的值越大即试验次数越多，结果越趋近于“正态分布”；
所以图331和332之间，前者效果“更好”；
且size足够大时，数据趋于稳定，不够大时，每次生成的结果差距也会比较明显（因为随机数据不一样）
（3）在p=0.5 时，分布无偏移；但是p=0.2或者p=0.8时，分布有偏移；详见333和334图

2. 固定p值，对比不同n值的结果

import matplotlib.pyplot as ply
import numpy as np

 # 产生二项分布的随机数并制作成直方图
def plot_binomial(n1,n2,p,size):
    # 使用同一套随机数
    np.random.seed(1)
    sample1 = np.random.binomial(n1,p,size)  
    sample2 = np.random.binomial(n2,p,size)  
    # 绘制直方图，设置标题和坐标，及图标
    labels=["sample1","sample2"]
    plt.hist(sample1, bins=n1, rwidth=0.6,alpha=0.6,label=labels) 
    plt.hist(sample2, bins=n2, rwidth=0.6,alpha=0.6,label=labels)
    plt.title('Binomial PMF with p={},size={}'.format(p,size))  
    plt.xlabel('number of successes')
    plt.ylabel('probability')
    # 展示图标和图形
    plt.legend()
    plt.show() 

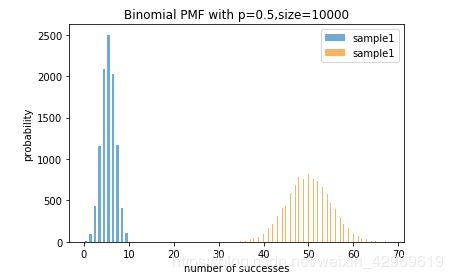
plot_binomial(10,100,0.5,10000)

说明：

两个图像都呈较好的“正态分布”；但是输入参数n=100时，“成功次数”可以取的值的范围也增加，样本数据的值域更宽；这也导致落其“正态分布”更平缓（只是单纯的分摊范围大，分担数量少而已，“方差”大小的形象下面会详细对比）

• numpy.random.normal(loc, scale, size)：正态分布

正态分布是一种很常用的统计分布，可以描述现实世界的很多事物，同时具备非常漂亮的性质，此处不做过多的介绍；除此之外，我们更经常会用到的numpy.random.randn(size)实际上就是标准正态分布（μ=0,σ=1）即numpy.random.normal(loc=0, scale=1, size)

import matplotlib.pyplot as ply
import numpy as np

# '''正态分布概率密度函数'''的实现
def norm_pdf(x,mu,sigma):
    pdf = np.exp(-((x - mu)**2) / (2* sigma**2)) / (sigma * np.sqrt(2*np.pi)) 
    return pdf

mu = 0    # 均值为0
sigma1 = 1 # 标准差为1
sigma2 = 3

# 生成数据 
sample1 = np.random.normal(loc=mu, scale=sigma1, size=10000)
sample2=np.random.normal(loc=mu,scale=sigma2,size=10000)
# 用统计模拟绘制正态分布的直方图
plt.figure(figsize=(10,8))
plt. hist(sample1, bins=100, alpha=0.3,density=True,label="sample1")    # 如果不使用density参数会导致无法呈现PDF曲线，因为pdf曲线Y轴小到无法在正态分布的直方图Y轴值下展示
plt.hist(sample2,bins=100,alpha=0.3,density=True,label="sample2")
# 根据正态分布的公式绘制PDF曲线
x = np.arange(-10, 10, 0.01)
y1 = norm_pdf(x, mu, sigma1)
y2 = norm_pdf(x,mu,sigma2)
plt.plot(x,y1,color='orange',lw=3)
plt.plot(x,y2,c='k',lw=2)

plt.legend()
plt.show()

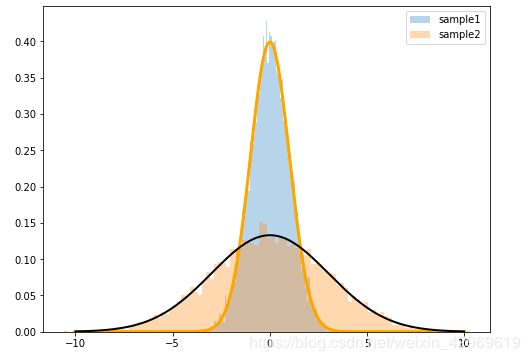
说明：

“方差”越大，分布越平缓