Quantopian教程系列三
Alphalens
lesson 1 Introduction
什么是alphalens?
- alphalens是一个用来分析给定alpha因子预测未来回报有效性的工具,需要提醒的是,alpha因子表达了某些给定信息集与未来回报之间的预测关系。
我们该什么时候使用alphalens?
-
在量化工作流程中,Alphalens被设计为早期和经常使用。一旦你定义了你的资产池并在pipeline中构造了一个因子,最好在回测前使用Alphalens来分析它。在量化工作流程的背景下:
1.定义您的交易领域,并建立一个阿尔法因子使用pipeline API。
2.分析阿尔法因子的预测能力。
3.使用optimal API在quant’ s IDE中创建基于您的阿尔法因子的交易策略。
4.用Pyfolio测试你的交易策略并分析结果。
在管道API教程中,您学习了如何定义一个交易领域并构建一个alpha因子。alphalens可以让你检查一个因子,看看它是如何预测的。第1步和第2步在研究笔记中完成,第3步和第4步在算法IDE中完成。
lesson 2 创建Creating Teaersheets
用 alphalens 创建tear sheets
- 在这节课中,你将学习如何使用它的四个步骤:
1.通过在一定时间内创建和运行一个pipeline来表达一个阿尔法因子并定义一个交易范围。
2.使用get_pricing()查询同一时间段交易范围中资产的定价数据
3.使用get_clean_factor_and_forward_returns()将alpha因子数据与定价数据对齐
4.使用create_full_tear_sheet()可视化alpha因子对未来价格走势的预测
建立和运行一个pipeline
- 下面的代码表示了一个基于资产增长的alpha因子,然后使用run_pipeline()运行它。
from quantopian.pipeline.data import factset
from quantopian.pipeline import Pipeline
from quantopian.research import run_pipeline
from quantopian.pipeline.filters import QTradableStocksUS
def make_pipeline():
# Measures a company's asset growth rate.
asset_growth = factset.Fundamentals.assets_gr_qf.latest
return Pipeline(
columns={'asset_growth': asset_growth},
screen=QTradableStocksUS() & asset_growth.notnull()
)
factor_data = run_pipeline(pipeline=make_pipeline(), start_date='2014-1-1', end_date='2016-1-1')
# Show the first 5 rows of factor data
factor_data.head(5)
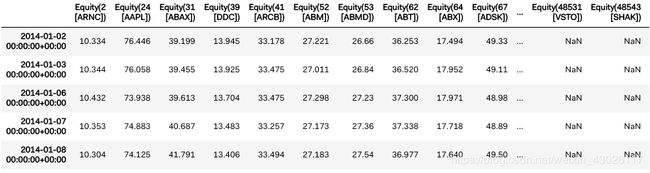
查询价格数据
- 现在我们有了因子数据,让我们得到相同时期的价格数据。get_pricing()返回指定时间段内资产列表的定价数据。它需要四个参数:
1.我们希望为其定价的资产列表。
2.开始日期。
3.结束日期。
4.是采用开盘价、高点、低点还是收盘价。
pricing_data = get_pricing(
symbols=factor_data.index.levels[1], # Finds all assets that appear at least once in "factor_data"
start_date='2014-1-1',
end_date='2016-2-1', # must be after run_pipeline()'s end date. Explained more in lesson 4
fields='open_price' # Generally, you should use open pricing. Explained more in lesson 4
)
# Show the first 5 rows of pricing_data
pricing_data.head(5)
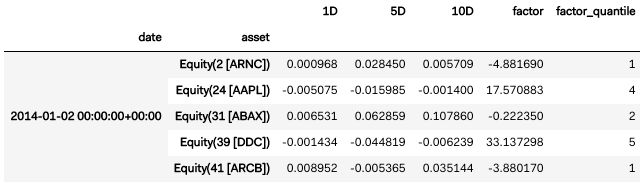
对其数据
- get_clean_factor_and_forward_returns()将来自pipeline的因子数据与来自get_pricing()的定价数据进行对齐,并返回一个适合使用Alphalens的图表函数进行分析的对象。它需要两个参数:
1.我们使用run_pipeline()创建的因子数据。
2.我们使用get_pricing()创建的定价数据。
from alphalens.utils import get_clean_factor_and_forward_returns
merged_data = get_clean_factor_and_forward_returns(
factor=factor_data,
prices=pricing_data
)
# Show the first 5 rows of merged_data
merged_data.head(5)
可视化回报
最后,将get_clean_factor_and_forward_returns()的输出传递给create_full_tear_sheet()。
lesson 3 interpreting tearsheets
在前一课中,您学习了如何查询和处理数据,以便我们能够使用Alphalens tear sheet分析数据。在本节课中,您将通过分析这些数据片来体验量化工作流的alpha发现阶段的几个迭代。在这节课中,我们将:
1.使用create_information_tear_sheet()分析alpha因子对未来价格走势的预测效果。
2.试着通过与另一个因子结合来改善我们原来的因子。
3.使用create_returns_tear_sheet()预览alpha因子的盈利能力。
我们的初始因子
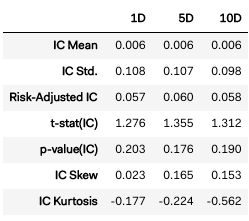
- 下面的代码根据公司的净收入和市值表达了一个alpha因子,然后为该alpha因子创建一个 information tear sheet。我们将通过查看它的信息系数(IC)来开始分析alpha因子。IC是一个从-1到1的数字,它量化了一个因子的可预测性。任何大于0的数都被认为具有一定的预测性。
- 首先要看的是IC均值,它是一个因子在给定时间段内的平均IC。你希望因子的IC均值尽可能高。一般来说,一个因子的IC均值是否大于0是值得研究的。如果在一个大的交易区间内,它的IC均值接近于。1(或更高),那么这个因素可能真的很好。
from quantopian.pipeline.data import factset
from quantopian.pipeline import Pipeline
from quantopian.research import run_pipeline
from quantopian.pipeline.factors import CustomFactor, SimpleMovingAverage
from quantopian.pipeline.filters import QTradableStocksUS
from alphalens.tears import create_information_tear_sheet
from alphalens.utils import get_clean_factor_and_forward_returns
def make_pipeline():
# 1 year moving average of year over year net income
net_income_moving_average = SimpleMovingAverage(
inputs=[factset.Fundamentals.net_inc_af],
window_length=252
)
# 1 year moving average of market cap
market_cap_moving_average = SimpleMovingAverage(
inputs=[factset.Fundamentals.mkt_val],
window_length=252
)
average_market_cap_per_net_income = (market_cap_moving_average / net_income_moving_average)
# the last quarter's net income
net_income = factset.Fundamentals.net_inc_qf.latest
projected_market_cap = average_market_cap_per_net_income * net_income
return Pipeline(
columns={'projected_market_cap': projected_market_cap},
screen=QTradableStocksUS() & projected_market_cap.notnull()
)
factor_data = run_pipeline(make_pipeline(), '2010-1-1', '2012-1-1')
pricing_data = get_pricing(factor_data.index.levels[1], '2010-1-1', '2012-2-1', fields='open_price')
merged_data = get_clean_factor_and_forward_returns(factor_data, pricing_data)
create_information_tear_sheet(merged_data)
下面是create_information_tear_sheet()生成的第一个图表。注意IC的平均值都是正的。这是一个好迹象!
增加另一个 alpha 因子
- 在量化工作流程的早期,Alphalens对于识别不具有预测性的alpha因子非常有用。这使您可以避免浪费时间在一个可能在流程早期被丢弃的因子上运行完整的回测。
- 下面的代码表达了另一个名为price_to_book的alpha因子,使用zscores和winsorization将它与’ projected_market_cap '组合在一起,然后根据新的(有望改进的)alpha因子创建另一个信息样本。
def make_pipeline():
# 1 year moving average of year over year net income
net_income_moving_average = SimpleMovingAverage(
inputs=[factset.Fundamentals.net_inc_af],
window_length=252
)
# 1 year moving average of market cap
market_cap_moving_average = SimpleMovingAverage(
inputs=[factset.Fundamentals.mkt_val],
window_length=252
)
average_market_cap_per_net_income = (market_cap_moving_average / net_income_moving_average)
net_income = factset.Fundamentals.net_inc_qf.latest # The last quarter's net income
projected_market_cap = average_market_cap_per_net_income * net_income
price_to_book = factset.Fundamentals.pbk_qf.latest # The alpha factor we are adding
factor_to_analyze = projected_market_cap.zscore() + price_to_book.zscore()
return Pipeline(
columns={'factor_to_analyze': factor_to_analyze},
screen=QTradableStocksUS() & factor_to_analyze.notnull()
)
factor_data = run_pipeline(make_pipeline(), '2010-1-1', '2012-1-1')
pricing_data = get_pricing(factor_data.index.levels[1], '2010-1-1', '2012-2-1', fields='open_price')
new_merged_data = get_clean_factor_and_forward_returns(factor_data, pricing_data)
create_information_tear_sheet(new_merged_data)
注意IC数字比第一个图表中的数字要低。这意味着我们添加的因素正在使我们的预测变得更糟!
看看我们的阿尔法因子是否有利可图
- 我们发现alpha因子的第一次迭代比第二次迭代具有更高的预测价值。我们看看原始的因子是否能赚钱。
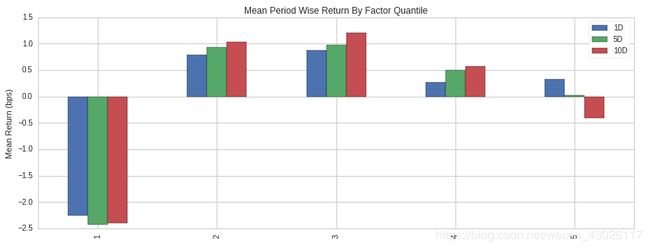
- create_returns_tear_sheet()将您的资产分割成分位数,然后显示每个分位数在不同时间段内生成的返回。分位数1是alpha因子值最低的资产的20%,分位数5是alpha因子值最高的20%。
- 这个函数创建了六种图表,但其中最重要的两种是:
Mean period-wise returns by factor quantile(因子分位数计算的周期平均回报率):这个图表显示了你的资产中每个分位数在每个时间段的平均回报率。你希望右边的分位数比左边的分位数有更高的平均回报率。
Cumulative return by quantile(分位数的累积回报):这个图表向您展示了每个分位数在一段时间内的表现。你希望看到分位数1持续表现最差,分位数5持续表现最好,其他分位数在中间。
下面的代码创建了一个返回的 returns tear sheet 。
from alphalens.tears import create_returns_tear_sheet
create_returns_tear_sheet(merged_data)
注意分位数5并没有最高的回报。理想情况下,您希望分位数1的回报率最低,而分位数5的回报率最高。此外,分位数图的累积收益中分位数之间存在显著的交叉。理想情况下,不应该有任何交叉。这张撕纸告诉我们,我们还有工作要做!

- 在这节课中,你经历了几个周期的阿尔法发现阶段的定量worfklow。制作好的alpha因子并不容易,但Alphalens允许您快速遍历它们,以确定您是否在正确的轨道上!你通常可以通过创造性地使用移动平均线、寻找趋势逆转或其他策略来以某种方式改进现有的阿尔法因子。
试着看看quant的论坛,或者阅读一些学术论文来寻找灵感。这就是你发挥创造力的地方!在下一课中,我们将讨论高级alphalens的概念。
Advanced Alphalens Concepts
- 你已经学习了使用 alphalens 基本知识。这节课探讨了以下高级 alphalens 的概念:
1.确定一个阿尔法因子的预测价值延伸到未来有多远。
2.处理一个名为maxlossdederror的常见Alphalens错误。
3.按部门对资产进行分组,然后分别对每个部门进行分析。
4.编写小组中性策略。
下面的代码在pipeline中创建一个alpha因子。本课的其余部分将讨论使用管道创建的数据的高级Alphalens概念。
重要提示:在本节课之前,我们将run_pipeline()的输出传递给get_clean_factor_and_forward_returns(),没有做任何更改。这是可能的,因为以前的课程的pipeline只返回一个列。本课的管道返回两列,这意味着我们需要指定作为factor数据传递的列。在下面的单元格中,查找get_clean_factor_and_forward_returns()附近的注释代码,以了解如何做到这一点。
from quantopian.pipeline import Pipeline
from quantopian.pipeline.data import factset
from quantopian.research import run_pipeline
from quantopian.pipeline.filters import QTradableStocksUS
from quantopian.pipeline.classifiers.fundamentals import Sector
from alphalens.utils import get_clean_factor_and_forward_returns
def make_pipeline():
change_in_working_capital = factset.Fundamentals.wkcap_chg_qf.latest
ciwc_processed = change_in_working_capital.winsorize(.2, .98).zscore()
sales_per_working_capital = factset.Fundamentals.sales_wkcap_qf.latest
spwc_processed = sales_per_working_capital.winsorize(.2, .98).zscore()
factor_to_analyze = (ciwc_processed + spwc_processed).zscore()
sector = Sector()
return Pipeline(
columns = {
'factor_to_analyze': factor_to_analyze,
'sector': sector,
},
screen = (
QTradableStocksUS()
& factor_to_analyze.notnull()
& sector.notnull()
)
)
pipeline_output = run_pipeline(make_pipeline(), '2013-1-1', '2014-1-1')
pricing_data = get_pricing(pipeline_output.index.levels[1], '2013-1-1', '2014-3-1', fields='open_price')
factor_data = get_clean_factor_and_forward_returns(
pipeline_output['factor_to_analyze'], # How to analyze a specific pipeline column with Alphalens
pricing_data,
periods=range(1,32,3)
)
Visualizing an alpha factor’s decay rate
- 很多基础数据一年只在季度报告中出现4次。由于频率较低,因此增加get_clean_factor_and_forward_returns()对未来进行预测以计算返回值的时间是很有用的。
提示:一个月通常有21个交易日,一个季度通常有63个交易日,一年通常有252个交易日。
假设你正在制定一项策略,购买利润不断增长的公司的股票(数据每63个交易日发布一次)。你会只看未来10天来分析这个因素吗?可能不是!但是,你如何决定向前走多远呢?
下面的代码显示了alpha因子随时间的IC均值。
from alphalens.performance import mean_information_coefficient
mean_information_coefficient(factor_data).plot(title="IC Decay");
- 这条线低于0的点表示阿尔法因子的预测不再有用。
提示:这是本课第二部分的设置。
factor_data = get_clean_factor_and_forward_returns(
pipeline_output['factor_to_analyze'],
pricing_data,
periods=range(1,252,20) # The third argument to the range statement changes the "step" of the range
)
mean_information_coefficient(factor_data).plot()
-运行上述代码将产生以下错误:
![]()
Dealing With MaxLossExceededError
- 噢,不!什么是maxlossdederror: max_loss(35.0%)超过88.4%,考虑增加它。的意思吗?
get_clean_factor_and_forward_returns()将来自alpha因子的数据与向前查找的返回数据进行对齐。这意味着,我们需要我们的定价数据比我们的阿尔法因子数据更深入地研究未来,至少在我们的预期周期内是如此。在本例中,我们将把get_pricing()的end_date参数更改为至少比run_pipeline()的end_date参数晚一年。
下面的代码展示了如何进行这些更改。
pipeline_output = run_pipeline(
make_pipeline(),
start_date='2013-1-1',
end_date='2014-1-1' # *** NOTE *** Our factor data ends in 2014
)
pricing_data = get_pricing(
pipeline_output.index.levels[1],
start_date='2013-1-1',
end_date='2015-2-1', # *** NOTE *** Our pricing data ends in 2015
fields='open_price'
)
factor_data = get_clean_factor_and_forward_returns(
pipeline_output['factor_to_analyze'],
pricing_data,
periods=range(1,252,20) # Change the step to 10 or more for long look forward periods to save time
)
mean_information_coefficient(factor_data).plot()
正如你所看到的,这个阿尔法因子的IC在几天后迅速衰减,但在未来六个月后甚至会变得更强。有趣!

注意:maxlossdederror有两个可能的原因;前向返回计算和终止。我们在这里展示了如何修正前向返回计算,因为它更常见。你可以在API文档中了解更多关于binning的知识。
Analyzing Alpha Factors By Group
- Alphalens允许您使用分类器对资产进行分组。一个常见的用例是创建一个分类器,该分类器指定每个股票属于哪个部门,然后比较各个部门之间的阿尔法因素的回报。
您可以根据任何分类器对资产进行分组,但是扇区是最常见的。本课程的第一个单元格中的pipeline将返回一个名为sector列,该列的值表示相应的晨星扇sector代码。我们现在要做的就是将该列传递给get_clean_factor_and_forward_returns()的groupby参数
下面的代码展示了如何进行这些更改。
from alphalens.tears import create_returns_tear_sheet
sector_labels, sector_labels[-1] = dict(Sector.SECTOR_NAMES), "Unknown"
factor_data = get_clean_factor_and_forward_returns(
factor=pipeline_output['factor_to_analyze'],
prices=pricing_data,
groupby=pipeline_output['sector'],
groupby_labels=sector_labels,
)
create_returns_tear_sheet(factor_data=factor_data, by_group=True)
一旦因子按部门分组,您将在tear sheet底部看到图表,显示我们的因子在不同部门的表现。
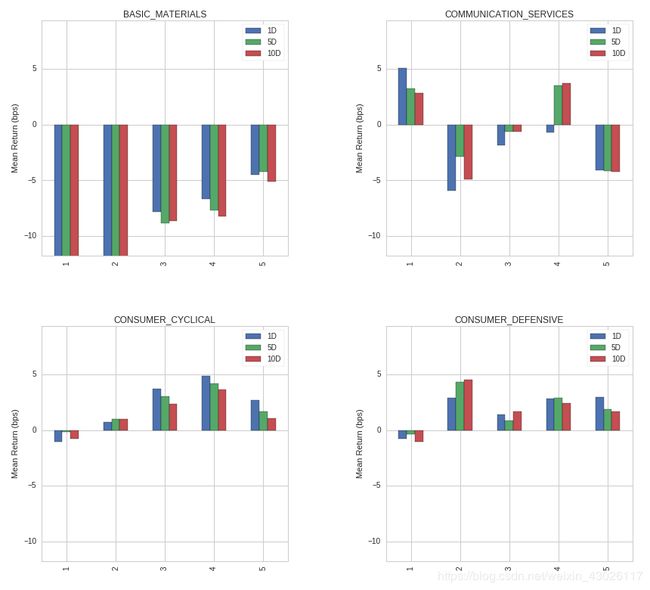
Writing Group Neutral Strategies
- Alphalens不仅允许我们模拟我们的alpha因素在多/空交易策略中的表现,它还允许我们模拟我们在每个组中做多/空时的表现!
按行业分组,对每个行业做多/做空,可以限制你对行业整体走势的敞口。例如,您可能已经注意到在本教程的第三步中,某些扇sector收益都是正的,或者都是负的。这些信息对我们毫无用处,因为这只意味着该行业的股票表现优于(或逊于)市场;它并没有给我们任何关于我们的因素在该部门中表现如何的洞察力。
由于我们在前一个单元中按部门对资产进行了分组,因此实现组中性很容易;只需做以下两个更改:
1.将binning_by_group=True作为参数传递给get_clean_factor_and_forward_returns()。
2.将group_neutral=True作为参数传递给create_full_tear_sheet()。
3.下面的细胞作了适当的改变。尝试运行它,并注意结果如何不同于前一个单元格。
factor_data = get_clean_factor_and_forward_returns(
pipeline_output['factor_to_analyze'],
prices=pricing_data,
groupby=pipeline_output['sector'],
groupby_labels=sector_labels,
binning_by_group=True,
)
create_returns_tear_sheet(factor_data, by_group=True, group_neutral=True)
正如你所看到的,当我们保持群体中立时,结果是不同的。有时候,你可以通过以一种群体中立的方式来分析你的阿尔法因子,从而洞察它为什么会以某种方式表现。

您在本教程中学习的技术将帮助您识别好的alpha因子。使用下面页面中的模板来创建一些alpha因子,然后尝试在IDE中实现它们,从而参加quantcontest !
Quickstart Template
Define An Alpha Factor
- 在下面的pipeline中,设置了附加的notebook来分析名为factor_to_analyze的alpha因子。
如果您感到困惑:不要担心,您只需要修改整个记事本中的一行代码就可以开始了!
尝试修改这行代码:factor_to_analyze = (current_assets - assets_moving_average),以便从FactSet的基本数据字段列表中分析一个数据字段。例如,您可以将这一行更改为factor_to_analyze = factset. basics .assets_gr_qf。最后,在笔记本中运行其余的单元格。通过修改这一行代码,您现在可以分析一家公司的资产增长如何影响其股票价格!
def make_pipeline():
assets_moving_average = SimpleMovingAverage(inputs=[factset.Fundamentals.assets], window_length=252)
current_assets = factset.Fundamentals.assets.latest
factor_to_analyze = (current_assets - assets_moving_average)
sector = Sector()
return Pipeline(
columns={'factor_to_analyze': factor_to_analyze, 'sector': sector},
screen=QTradableStocksUS() & factor_to_analyze.notnull() & sector.notnull()
)
factor_data = run_pipeline(make_pipeline(), '2015-1-1', '2016-1-1')
pricing_data = get_pricing(factor_data.index.levels[1], '2015-1-1', '2016-6-1', fields='open_price')
Determine The Decay Rate Of The Alpha Factor
- 下表显示了alpha因子随时间的信息系数。需要提醒的是,IC是对给定阿尔法因子的预测能力进行量化的最有用的数字。
longest_look_forward_period = 63 # week = 5, month = 21, quarter = 63, year = 252
range_step = 5
merged_data = get_clean_factor_and_forward_returns(
factor=factor_data['factor_to_analyze'],
prices=pricing_data,
periods=range(1, longest_look_forward_period, range_step)
)
mean_information_coefficient(merged_data).plot(title="IC Decay")
Create Group Neutral Tear Sheets
- 运行以下单元格,为您的阿尔法因子创建组中性tear sheet。如果您不知道group neutral是什么意思,请参阅本教程的第4课。
理想情况下,您希望IC平均线图始终高于0。您还希望看到分位数1始终具有最低的回报,而分位数5始终具有最高的回报。
最后,一定要看一下IC的平均值和按行业划分的回报率,看看在业绩方面是否有重大的异常值。
sector_labels, sector_labels[-1] = dict(Sector.SECTOR_NAMES), "Unknown"
merged_data = get_clean_factor_and_forward_returns(
factor=factor_data['factor_to_analyze'],
prices=pricing_data,
groupby=factor_data['sector'],
groupby_labels=sector_labels,
binning_by_group=True,
periods=(1,5,10)
)
create_information_tear_sheet(merged_data, by_group=True, group_neutral=True)
create_returns_tear_sheet(merged_data, by_group=True, group_neutral=True)