【一文读懂卷积神经网络（二）】可能是你看过的最全的CNN（步长为1，有填充）

本系列将由浅入深的介绍卷积神经网络的前向传播与后向传播，池化层的前向传播与后向传播，并分别介绍在不同步长与不同填充的情况下卷积层和池化层的前向传播与后向传播又有哪些不同。最后给出完整的Python实现代码。

完整目录如下：

一、CNN$\Rightarrow$步长为1，无填充的卷积神经网络

二、CNN$\Rightarrow$步长为1，有填充的卷积神经网络

三、CNN$\Rightarrow$步长不为1，无填充的卷积神经网络

四、CNN$\Rightarrow$步长不为1，有填充的卷积神经网络

上一篇文章已经介绍了无填充，步长为1的卷积神经网络,本文将继续由浅入深的介绍有填充，步长为1的卷积神经网络的前向传播与后向传播，有填充的池化层的前向传播与后向传播。

1.CNN的前向传播（有填充，步长strides=1）

1.1 何为填充

在上一节无填充，步长为1的卷积神经网络中我们介绍了卷积和池化的原理，这里不再赘述，让我们看看什么是填充。首先回顾一下上一节介绍的卷积层的正向传播。

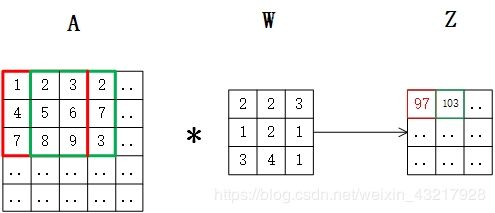
可以看到输入5x5的矩阵A，输出的是3x3的矩阵Z，因为步长为1，且没有填充，所以导致Z的大小比A小，有些时候我们并不想让输出的维度减小或者是减小太多（比如深层次神经网络里，如果一直减小下去到最后维度会非常非常小），那怎么办呢，这时候我们就可以使用填充(padding)。
填充，顾名思义，就是在输入矩阵A的外面填充1层或多层，这个由自己决定。卷积后的维度由 $n_H=\lfloor \frac{n_{Hprev}-f+2\times pad}{strides}\rfloor +1$计算，其中$n_{Hprev}$为卷积前输入图像的高度，f为卷积核的大小，strides为卷积的步长，pad为填充值，$n_H$为卷积后输出图像的高度，要使卷积前后输入输出大小不变，我们需要设定填充值为$pad=\frac{strides\times (n_H-1)-n_{Hprev}+f}{2}$.
接下来我们看看有填充的卷积层和池化层的正向传播。

1.2 有填充的卷积层

对于输入3x3的矩阵A，给定3x3的卷积核，要想使输出的矩阵Z的大小和A相同，我们对A做填充，填充的大小为$pad=\frac{1\times (3-1)-3+3}{2}=1$，所以我们对A上下左右分别作1行（列）的填充。卷积示意图如下（本文中默认卷积步长都为1）。

1.3 有填充的池化层

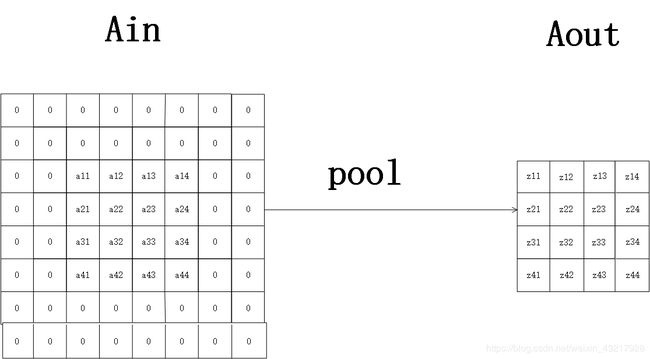
对于输入4x4的矩阵$A_{in}$，给定2x2的池化核，步长为2，要想使输出矩阵$A_{out}$的大小和$A_{in}$相同，我们需要对$A_{in}$做填充，填充的大小为$pad=\frac{2\times (4-1)-4+2}{2}=2$，所以我们需要对$A_{in}$上下左右分别做两行（列）填充。池化示意图如下。

2.CNN的反向传播（有填充，步长strides=1）

2.1 池化层的反向传播

对于池化层的反向传播，我们依然是分为最大池化和均值池化两种情况来分别讲述。首先看看最大池化的反向传播。

2.1.1 最大池化的反向传播

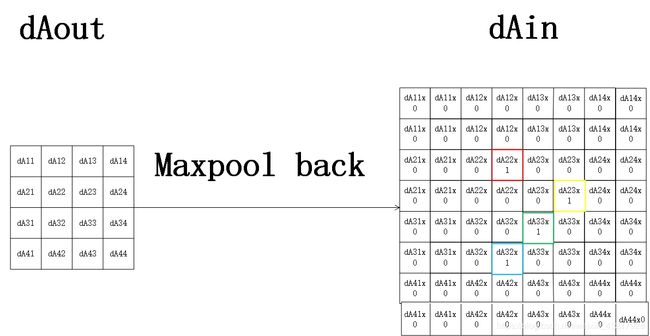
对于有填充，步长为2的最大池化，我们假设下图彩色方框框出的值为一个池化区域内最大的值。

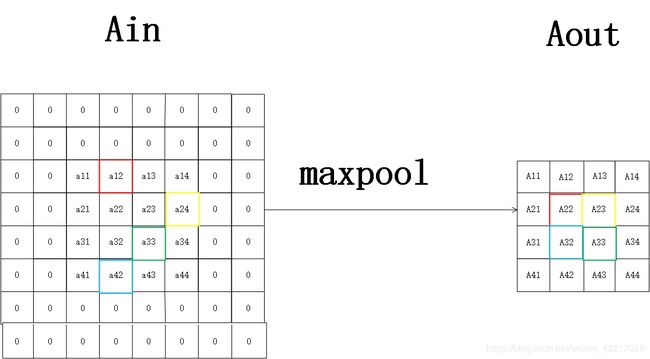
我们可得
A11 = 0 , A12 = 0 , A13 = 0 , A14 = 0
A21 = 0
$A22=0\times a11+1\times a12+0\times a21+0\times a22$
$A23=0\times a13+0\times a14+0\times a23+1\times a24$
$A32=0\times a31+0\times a32+0\times a41+1\times a42$
$A33=1\times a33+0\times a34+0\times a43+0\times a44$
A34 = 0
A41 = 0 , A42 = 0 , A43 = 0 , A44 = 0

有填充的最大池化反向传播见下图。

即$d{A}_{in}^1=delete\_pad(upsample(d{A}_{out}^1))$，，先像无填充的最大池化反向传播那样还原dAin_paded，再对dAin_paded做删除填充操作得到dAin_paded（本文中填充pad为2）
以下给出本方法的Python实现（假定输入一个数据，且为单通道）

    def max_pool_backward(self,dAout,Ain,filterSize,strides,padSize):
    	#params说明
    	#params dAout为传入的dAout
    	#params Ain为我们记录的正向传播时当前层池化的输入，我们将用来它来计算每个池化核区域内的最大值
    	#params filterSize为池化核的大小
    	#params strides为池化层的步长
    	#params padSize为要填充的大小
    	#return dAin
        dAin=np.zeros_like(Ain)  #初始化dAin为shape和Ain相同，值为0的矩阵
        n_H,n_W=dAout.shape   #n_H,n_W分别是dAout的高和宽
        for h in range(n_H):   #遍历行
             for w in range(n_W):  #遍历列
                     h_start=h*strides  #当前池化区域行的开头
                     h_end=h_start+filterSize  #当前池化区域行的结尾
                     w_start=w*strides  #当前池化区域列的开头
                     w_end=w_start+filterSize  #当前池化区域列的结尾
                     mask=(Ain[h_start:h_end,w_start:w_end]==np.max(Ain[h_start:h_end,w_start:w_end]))
                     #找到当前池化区域内最大值的位置，在mask内，最大值的位置将会等于True(1)，其他位置都等于False(0)
                     dAin[h_start:h_end,w_start:w_end]=mask*dAout[h,w]  #实现对dAout的upsample
		dAin=np.pad(dAin,(padSize,padSize),'constant')   #对dAin填充
        return dAin
        
    def delete_pad(self,dA,pad_size):
    	#params说明
    	#params dA为传入的需要去掉填充的参数
    	#params pad_size为正向传播时填充的大小，是一个tuple，分别保存了行和列方向上填充的大小
    	#return dA
        pad_h_size,pad_w_size=pad_size  #填充的大小
        m,n_H_prev,n_W_prev,n_C=dA.shape  #填充后的大小
        #计算出填充前的大小
        n_H=n_H_prev-2*pad_h_size
        n_W=n_W_prev-2*pad_w_size
        #需要删除的行和列的list
        delete_h_list=[h for h in range(pad_h_size)]
        delete_w_list=[w for w in range(pad_w_size)]
        for i in range(pad_h_size):
            delete_h_list.append((i+n_H+pad_h_size))
        for j in range(pad_w_size):
            delete_w_list.append((j+n_W+pad_w_size))

        dA=np.delete(dA,delete_h_list,axis=1)
        dA=np.delete(dA,delete_w_list,axis=2)

        return dA

2.1.2 均值池化的反向传播

由上面的最大池化反向传播的结论可知，有填充的均值池化的反向传播就是先像无填充的均值池化反向传播那样还原dAin，再对dAin做删除填充操作（本文中填充pad为2）
以下给出本方法的Python实现（假定输入一个数据，且为单通道）

def average_pool_backward(self,dAout,Ain,filterSize,strides,padSize):
    	#params说明
    	#params dAout为传入的dAout
    	#params Ain为我们记录的正向传播时当前层池化的输入，我们将用来它来计算每个池化核区域内的平均值
    	#params filterSize为池化核的大小
    	#params strides为池化层的步长
    	#params padSize为要填充的大小
    	#return dAin
        dAin = np.zeros_like(Ain)  #初始化dAin为shape和Ain相同，值为0的矩阵
        n_H, n_W = dAout.shape  #n_H,n_W分别是dAout的高和宽
        for h in range(n_H):  #遍历行
             for w in range(n_W):  #遍历列
                     h_start = h * strides  #当前池化区域行的开头
                     h_end = h_start + filterSize  #当前池化区域行的结尾
                     w_start = w * strides  #当前池化区域列的开头
                     w_end = w_start + filterSize  #当前池化区域列的结尾
                     dAin[h_start:h_end,w_start:w_end]+=np.ones((filterSize,filterSize))*(dAout[h,w]/(filterSize**2))
                     #1/(filterSize**2)为池化区域内对每个值的导数，再将它上采样至池化核的大小
		dAin=np.pad(dAin,(padSize,padSize),'constant')  #对dAin填充
        return dAin
        
    def delete_pad(self,dA,pad_size):
    	#params说明
    	#params dA为传入的需要去掉填充的参数
    	#params pad_size为正向传播时填充的大小，是一个tuple，分别保存了行和列方向上填充的大小
    	#return dA
        pad_h_size,pad_w_size=pad_size  #填充的大小
        m,n_H_prev,n_W_prev,n_C=dA.shape  #填充后的大小
        #计算出填充前的大小
        n_H=n_H_prev-2*pad_h_size
        n_W=n_W_prev-2*pad_w_size
        #需要删除的行和列的list
        delete_h_list=[h for h in range(pad_h_size)]
        delete_w_list=[w for w in range(pad_w_size)]
        for i in range(pad_h_size):
            delete_h_list.append((i+n_H+pad_h_size))
        for j in range(pad_w_size):
            delete_w_list.append((j+n_W+pad_w_size))

        dA=np.delete(dA,delete_h_list,axis=1)
        dA=np.delete(dA,delete_w_list,axis=2)

        return dA

2.2 卷积层的反向传播

对于有填充的卷积层的反向传播，我们依然是要求dW，dA，db三个值。当求得dW，db后，就可以选用梯度下降法，Adam等优化算法来更新参数，直至满足停止条件最终得到模型。
首先来看看如何求dW。

2.2.1 求dW

我们先来回顾一下步长为1，有填充的卷积层是怎样的。

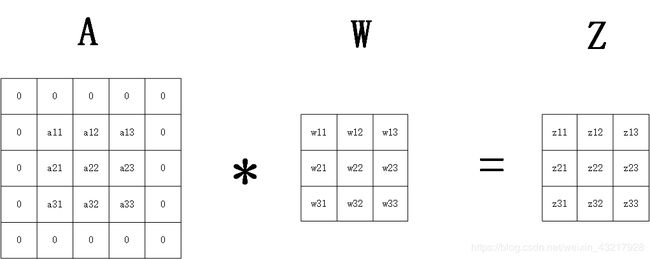
我们可以得到
$z11=0\times w11+0\times w12+0\times w13+0\times w21+a11\times w22+a12\times w23+0\times w31+a21\times w32+a22\times w33$
$z12=0\times w11+0\times w12+0\times w13+a11\times w21+a12\times w22+a13\times w23+a21\times w31+a22\times w32+a23\times w33$
$z13=0\times w11+0\times w12+0\times w13+a12\times w21+a13\times w22+0\times w23+a22\times w31+a23\times w32+0\times w33$
$z21=0\times w11+a11\times w12+a12\times w13+0\times w21+a21\times w22+a22\times w23+0\times w31+a31\times w32+a32\times w33$
$z22=a11\times w11+a12\times w12+a13\times w13+a21\times w21+a22\times w22+a23\times w23+a31\times w31+a32\times w32+a33\times w33$
$z23=a12\times w11+a13\times w12+0\times w13+a22\times w21+a23\times w22+0\times w23+a32\times w31+a33\times w32+0\times w33$
$z31=0\times w11+a21\times w12+a22\times w13+0\times w21+a31\times w22+a32\times w23+0\times w31+0\times w32+0\times w33$
$z32=a21\times w11+a22\times w12+a23\times w13+a31\times w21+a32\times w22+a33\times w23+0\times w31+0\times w32+0\times w33$
$z33=a22\times w11+a23\times w12+0\times w13+a32\times w21+a33\times w22+0\times w23+0\times w31+0\times w32+0\times w33$

所以
$dw11=dz22\times a11+dz23\times a12+dz32\times a21+dz33\times a22$
$dw12=dz21\times a11+dz22\times a12+dz23\times a13+dz31\times a21+dz32\times a22+dz33\times a23$
$dw13=dz21\times a12+dz22\times a13+dz31\times a22+dz32\times a23$

$dw21=dz12\times a11+dz13\times a12+dz22\times a21+dz23\times a22+dz32\times a31+dz33\times a32$
$dw22=dz11\times a11+dz12\times a12+dz13\times a13+dz21\times a21+dz22\times a22+dz23\times a23+dz31\times a31+dz32\times a32+dz33\times a33$
$dw23=dz11\times a12+dz12\times a21+dz21\times a22+dz22\times a23+dz31\times a32+dz32\times a33$

$dw31=dz12\times a21+dz13\times a22+dz22\times a31+dz23\times a32$
$dw32=dz11\times a21+dz12\times a22+dz13\times a23+dz21\times a31+dz22\times a32+dz23\times a33$
$dw33=dz11\times a22+dz12\times a23+dz21\times a32+dz22\times a33$

又是麻烦的数学公式，我们用一张简洁的示意图来表达。

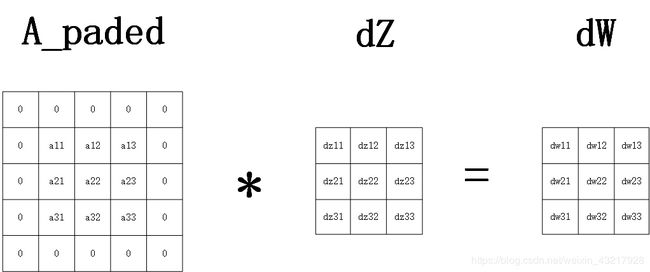
即$dW=A_{paded}\ast dZ$，由此可见，我们只需要在前向传播时将填充后的输入矩阵A记录下来，在反向传播时将它与dZ做步长为1的卷积，即可计算得到dW。
以下给出本方法的Python实现（假定输入一个数据，且为单通道）

def conv_backward(self,dZ,Aout_paded,filterSize,strides):   #卷积层的后向传播
    	#params说明
    	#params dZ传入的对当前卷积层输出的导数
    	#params Aout_paded当前卷积层正向传播时做了填充后的输入，我们用它来与dZ做卷积
    	#params filterSize卷积核的大小
    	#params strides卷积的步长
    	#return dW
        dW=np.zeros((filterSize,filterSize))  #初始化dW
        for m in range(filterSize):  #遍历行
            for n in range(filterSize):  #遍历列
                h_start = m * strides  #当前卷积区域行的开头
                h_end = h_start + filterSize  #当前卷积区域行的结尾
                w_start = n * strides  #当前卷积区域列的开头
                w_end = w_start + filterSize  #当前卷积区域列的结尾
                dW[m,n]+=np.sum(np.multiply(Aout_paded[h_start:h_end,w_start:w_end],dZ))
        return dW

2.2.2 求dA

由求dW这一节的数学公式我们可得
$da11=dz11\times w22+dz21\times w12+dz22\times w11$
…
…
因式子太长就不一一写了，读者可以自己完成试试。同样把这些繁琐的数学公式表示为一张生动的图片。

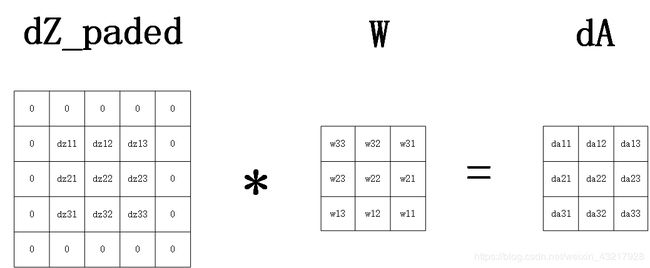
即$dA=pad(dZ)\ast rot180(W)$，由此可见，我们只需对dZ做前向传播时和上一层$A_{out}$一样的填充，再对沿顺时针180度旋转后的W做步长为1的卷积，即可完成dA的计算。
以下给出本方法的Python实现（假定输入一个数据，且为单通道）

 	def conv_backward(self,dZ_paded,Aout,convFilter,filterSize,strides,padSize):   #卷积层的后向传播
    	#params说明
    	#params dZ_paded传入的填充过后的对当前卷积层输出的导数
    	#params Aout正向传播时该层的输入，上层的输出
    	#params convFilter当前卷积层正向传播时的卷积核
    	#params filterSize卷积核的大小
    	#params strides卷积的步长
    	#params padSize正向传播时上一层Aout填充的大小
    	#return dA
        convFilter=convFilter[:,:,::-1,::-1]
		n_H_prev,n_W_prev = Aout.shape   #Aout的高和宽
        dA=np.zeros_like(Aout)   #初始化dA和Aout一样的shape，数值为0
		dZ_paded=np.pad(dZ,(padSize,padSize),'constant') #对dZ做填充，填充大小为filterSize-1，填充的值为0
        for h in range(n_H_prev): 
             for w in range(n_W_prev): 
                  dA[h,w]=np.sum(np.multiply(dZ_paded[h:h+filterSize,w:w+filterSize],convFilter))   #卷积操作
       	return dA
        
    def delete_pad(self,dA,pad_size):
    	#params说明
    	#params dA为传入的需要去掉填充的参数
    	#params pad_size为正向传播时填充的大小，是一个tuple，分别保存了行和列方向上填充的大小
    	#return dA
        pad_h_size,pad_w_size=pad_size  #填充的大小
        m,n_H_prev,n_W_prev,n_C=dA.shape  #填充后的大小
        #计算出填充前的大小
        n_H=n_H_prev-2*pad_h_size
        n_W=n_W_prev-2*pad_w_size
        #需要删除的行和列的list
        delete_h_list=[h for h in range(pad_h_size)]
        delete_w_list=[w for w in range(pad_w_size)]
        for i in range(pad_h_size):
            delete_h_list.append((i+n_H+pad_h_size))
        for j in range(pad_w_size):
            delete_w_list.append((j+n_W+pad_w_size))

        dA=np.delete(dA,delete_h_list,axis=1)
        dA=np.delete(dA,delete_w_list,axis=2)

        return dA

2.2.3 求db

求db跟无填充时一样，db=sum(dZ)。
以下给出本方法的Python实现（假定输入一个数据，且为单通道）

 def conv_backward(self,dZ):   #卷积层的后向传播 
        db=np.sum(dZ)
        return db

对有填充，步长为1的卷积神经网络的介绍就到此结束，可以发现有无填充的区别只是在前向和反向传播时是否要填充，下一节我们将介绍步长不为1，无填充的卷积神经网络。

所有源代码在文末

码字作图实属不易，前前后后断断续续用了不少时间，希望大家看后能有所收获，觉得可以的给点赞赏，让我有走下去的动力。谢谢大家！

大家看完python实现的方法是否会发现效率过于低下，因为其中有大量的for循环，博主本人花费了一些时间优化了代码，使速度有了很大的提升（最快的由6个for循环降为2个for循环），有兴趣的小伙伴可以在打赏我后评论或私聊我，我将代码发给你。请见谅。

3. 全部代码

Github见所有Python代码