没有多余的废话,直接上方案吧!
方案一:
最笨的方案即:for * for,对应的时间复杂度为:O(n*n)
画外音:比较笨的方法。
方案二:
有序 list 求交集,可以使用拉链法,即如下图所示:
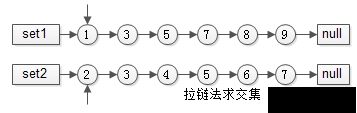
有序集合1:{1,3,5,7,8,9}
有序集合2:{2,3,4,5,6,7}
两个指针指向首元素,比较元素的大小:
(1)如果相同,放入结果集,随意移动一个指针;
(2)否则,移动值较小的一个指针,直到队尾;
这种方法的好处是:
(1)集合中的元素最多被比较一次,时间复杂度为:O(n);
(2)多个有序集合可以同时进行,这适用于多个分词的 item 求 url_id 交集;
这个方法就像一条拉链的两边齿轮,一一比对就像拉链,故称为拉链法;
画外音:倒排索引是提前初始化的,可以利用“有序”这个特性。
方案三:
数据量大时,【url_id 分桶水平切分 + 并行运算】 是一种常见的优化方法
如果能将 list1
举例:
有序集合1:{1,3,5,7,8,9, 10,30,50,70,80,90}
有序集合2:{2,3,4,5,6,7, 20,30,40,50,60,70}
求交集,先进行分桶拆分:
桶1的范围为 [1, 9]
桶2的范围为 [10, 100]
桶3的范围为 [101, max_int]
于是:
集合1就拆分成:
集合a:{1,3,5,7,8,9} 、集合b:{10,30,50,70,80,90} 、集合c:{}
集合2就拆分成:
集合d:{2,3,4,5,6,7} 、集合e:{20,30,40,50,60,70} 、集合f:{}
每个桶内的数据量大大降低了,并且每个桶内没有重复元素,可以利用多线程并行计算:
桶1内的 集合a 和 集合d 的交集是:x{3,5,7}
桶2内的 集合b 和 集合e 的交集是:y{30, 50, 70}
桶3内的 集合c 和 集合d 的交集是:z{}
最终,集合1和集合2的交集,是x与y与z的并集,即集合{3,5,7,30,50,70}。
画外音:多线程、水平切分都是常见的优化手段。
方案四:
bitmap 再次优化。
数据进行了水平分桶拆分之后,每个桶内的数据一定处于一个范围之内,如果集合 符合这个特点,就可以使用 bitmap 来表示集合:
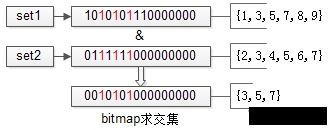
如上图,假设 set1:{1,3,5,7,8,9} 和 set2:{2,3,4,5,6,7} 的所有元素都在桶值 [1, 16] 的范围之内,可以用16个bit来描述这两个集合
原集合中的元素 x,在这个 16 bitmap 中的第x个 bit 为 1,此时两个 bitmap 求交集,只需要 将两个bitmap进行“与”操作,结果集bitmap的 3,5,7 位是1,表明原集合的交集为:{3,5,7}。
水平分桶,bitmap优化之后,能极大提高求交集的效率,但时间复杂度仍旧是O(n)。bitmap需要大量连续空间,占用内存较大。
画外音:bitmap能够表示集合,用它求集合交集速度非常快。
方案五:
有序链表集合求交集,跳表是最常用的数据结构,它可以将有序集合求交集的复杂度由 O(n) 降至 接近O(log(n))
集合1:{1,2,3,4,20,21,22,23,50,60,70}
集合2:{50,70}
要求交集,如果用拉链法,会发现 1,2,3,4,20,21,22,23 都要被无效遍历一次,每个元素都要被比对,时间复杂度为O(n),能不能 每次比对“跳过一些元素” 呢?
跳表就出现了:
集合1:{1,2,3,4,20,21,22,23,50,60,70} 建立跳表时,一级只有 {1,20,50} 三个元素,二级与普通链表相同。
集合2:{50,70} 由于元素较少,只建立了一级普通链表。
如此这般,在实施“拉链”求交集的过程中,set1 的指针能够由 1 跳到 20 再跳到 50,中间能够跳过很多元素,无需进行一一比对,跳表求交集的时间复杂度近似 O(log(n))
这是搜索引擎中常见的算法。
结语: