算法导论学习笔记15_最短路径
最短路径
- 1. 单源最短路径
- 1.1 Bellman-Ford算法
- 1.2 有向无环图的单源最短路径
- 1.3 Dijkstra算法
- 2. 所有结点对的最短路径问题
- 2.1 Floyd-Warshall算法
- 3. 算法实现(C++)
- 3.1 Bellman-Ford算法
- 3.2 有向无环图的单源最短路径
- 3.3 Dijkstra算法
- 3.4 Floyd算法
1. 单源最短路径
1.1 Bellman-Ford算法
Bellman-Ford算法解决一般情况下的单源最短路径问题,这里边的权重可以是负值。当最短路径不存在是,Ford算法可以识别出来。
Bellman-Ford算法通过对边进行松弛操作来渐近地从源结点s到每个结点v的最短路径的估计值,直到该估计值与实际的最短路径权重相同时为止。
Bellman-Ford算法的伪代码如下:
BELLMAN-FORD(G, w, s)
INITIALIZE-SINGLE-SOURCE(G.s)
for i = 1 to | G.V | - 1
for each edge(u, v)∈G.E
RELAX(u, v, w)
for each edge(u, v) ∈ G.E
if v.d > u.d + w(u, v)
return FALSE;
return TRUE;
其中,结点u包含两个额外属性:d和p,分别表示该结点到源结点s的距离的估计和该结点在最短路径上的父结点的估计。
因此,INITIALIZE-SINGLE-SOURCE的操作是对这两个属性进行初始化:
INITIALIZE-SINGLE-SOURCE(G.s)
for each vertex v ∈ G.V
v.d = ∞
v.p = NIL
s.d = 0
此外,上述RELAX就是求最短路径中最常用的松弛操作:
RELAX(u, v, w)
if v.d > u.d + w
v.d = u.d + w
v.p = u
因此,Bellman-Ford算法实际上就是对所有的边进行了N-1边松弛操作,最后求得源结点s到任意结点u的最短距离u.d。
Bellman-Ford算法的总运行时间为O(VE)。
1.2 有向无环图的单源最短路径
Bellman-Ford解决的是一般情况下的单源最短路径,然而很多时候图满足一些条件,例如不包含环,不包含负值等。这个时候可对算法效率进行提升。
根据结点的拓扑排序来对带权重的有向无环图进行边的松弛操作,可以在θ(V + E)时间内计算出从单个源结点到所有结点之间的最短路径。
算法的伪代码如下:
DAG-SHORTEST-PATHS(G, w, s)
topologically sort the vertices of G
INITALIZE-SINGLE-SOURCE(G, s)
for each vertex u, taken in topoigitcally soted order
for each vertex v ∈ G.Adj[u]
RELAX(u, v, w)
可以看出,上述代码中松弛的次数从Bellman-Ford算法的|G.V - 1| * |G.E|次减少到了|G.E|次。而增加的拓扑排序操作的时间复杂度为θ(V + E)。因此,该算法的总运行时间为θ(V + E)。
1.3 Dijkstra算法
当图满足所有的边的权重不为负值时(实际上很多情况下都满足这个性质),Dijkstra算法往往性能比Bellman-Ford的性能好。
Dijkstra算法在运行过程中维护的关键信息是一组结点集合S。从源结点s到该集合中每个结点之间的最短路径已经找到。算法重复从结点集V-S中选择最短路径估计最小的结点u,将u加入到集合S,然后对所有从u发出的边进行松弛。
Dijkstra算法的伪代码如下:
DIJKSTRA(G, w, s)
INITIALIZE-SINGLE-SOURCE(G, s)
S = φ
Q = G.V
while Q ≠ φ
u = EXTRACT-MIN(Q)
S = S ∪ {u}
for each vertex in G.Adj[u]
RELAX(u, v, w)
因为Dijkstra算法总是选择集合V-S中最近的结点来加入到集合S中,该算法使用的是贪心策略。
值得注意的是,为了提升算法的性能,上述代码中的Q往往用优先队列实现,队列的头部保留着集合V-S中路径估计最小的结点。
此外,由于松弛操作会改变集合V-S中的结点的d和p属性,此时应该更新优先队列Q,因此这里的松弛操作与Bellman-Ford算法中的松弛操作会略有不同,具体可见附录代码。
2. 所有结点对的最短路径问题
2.1 Floyd-Warshall算法
Floyd-Warshall算法是一种动态规划算法,它可以计算所有结点之间的最短路径。
伪代码如下:
FLOYD-WARSAHLL(w)
n = W.rows
Initialize distance matrix D
for k = 1 to n
for i = 1 to n
for j = 1 to n
Dij = min(Dij, Dik + Dkj)
return D
可以看到,Floyd算法非常的简洁,主程序只有三层的for循环,通过自底向上计算最短路径,最后得到所以结点之间的最短路径。
3. 算法实现(C++)
3.1 Bellman-Ford算法
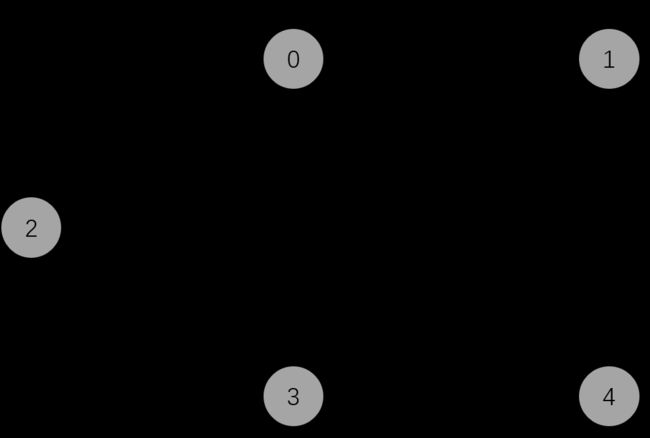
对于如下带环和负值的有向图:
利用Bellman-Ford算法求解从以结点2为源的的最短路径代码如下:
#include 输出为:
0 <- 1 <- 3 <- 2
1 <- 3 <- 2
2
3 <- 2
4 <- 0 <- 1 <- 3 <- 2
3.2 有向无环图的单源最短路径
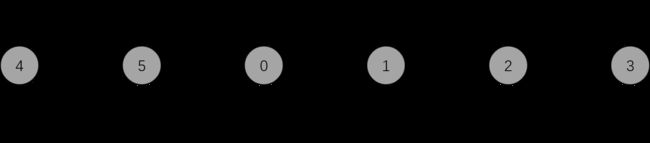
对于下面带负值的有向无环图:
可以首先对图中的所有结点进行拓扑排序,然后对于所有的结点,按照拓扑的顺序对其之后的所有边进行松弛操作。
代码如下:
#include
#include 输出为:
4
5 <- 4
0 <- 4
1 <- 0 <- 4
2 <- 0 <- 4
3 <- 0 <- 4
3.3 Dijkstra算法
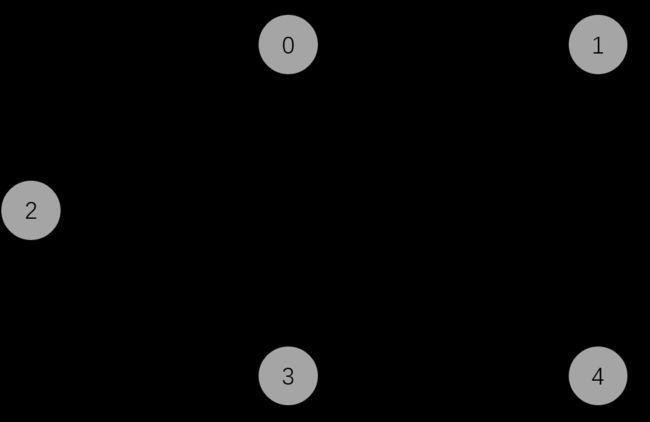
Dijkstra可用于不带负权值的图,例如下图:
代码:
#include 输出为:
0 <- 3 <- 2
1 <- 0 <- 3 <- 2
2
3 <- 2
4 <- 3 <- 2
3.4 Floyd算法
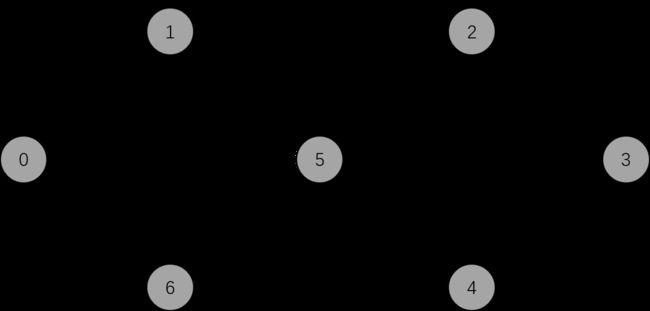
Floyd算法可用于计算图中所有结点之间的距离, 如下图:
代码:
#include 输出为:
0 -> 5 -> 4 -> 3