#数据结构#第七章:查找

单选题

2-1.已知一个长度为16的顺序表L，其元素按关键字有序排列。若采用二分查找法查找一个L中不存在的元素，则关键字的比较次数最多是：

A.4
B.5
C.6
D.7

B,log₂n + 1

2-2.用二分查找从100个有序整数中查找某数，最坏情况下需要比较的次数是：

A.7
B.10
C.50
D.9

A,└log₂n + 1

2-3.在有n（n>1000）个元素的升序数组A中查找关键字x。查找算法的伪代码如下所示：

k = 0;
while ( k<n 且 A[k]<x )  k = k+3;
if ( k<n 且 A[k]==x )  查找成功;
else if ( k-1<n 且 A[k-1]==x ) 查找成功;
     else if ( k-2<n 且 A[k-2]==x ) 查找成功;
          else 查找失败;

本算法与二分查找（折半查找）算法相比，有可能具有更少比较次数的情形是：

A.当x不在数组中
B.当x接近数组开头处
C.当x接近数组结尾处
D.当x位于数组中间位置

B

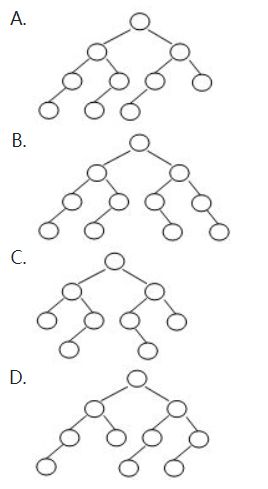
2-4.下列二叉树中，可能成为折半查找判定树（不含外部结点）的是:

A，一个介绍博客指路

2-5.若二叉搜索树是有N个结点的完全二叉树，则不正确的说法是：
A.所有结点的平均查找效率是O(logN)
B.最小值一定在叶结点上
C.最大值一定在叶结点上
D.中位值结点在根结点或根的左子树上

C

2-6.若一棵二叉树的后序遍历序列是{ 1, 3, 2, 6, 5, 7, 4 }，中序遍历序列是{ 1, 2, 3, 4, 5, 6, 7 }，则下列哪句是错的？

A.这是一棵完全二叉树
B.2是1和3的父结点
C.这是一棵二叉搜索树
D.7是5的父结点

A

2-7.将{ 32, 2, 15, 65, 28, 10 }依次插入初始为空的二叉搜索树。则该树的前序遍历结果是：

A.2, 10, 15, 28, 32, 65
B.32, 2, 10, 15, 28, 65
C.10, 28, 15, 2, 65, 32
D.32, 2, 15, 10, 28, 65

D

2-8.若一棵二叉树的前序遍历序列是{ 4, 2, 1, 3, 6, 5, 7 }，中序遍历序列是{ 1, 2, 3, 4, 5, 6, 7 }，则下列哪句是错的？

A.这是一棵完全二叉树
B.所有的奇数都在叶子结点上
C.这是一棵二叉搜索树
D.2是5的父结点

D

2-9.将{ 5, 11, 13, 1, 3, 6 }依次插入初始为空的二叉搜索树。则该树的后序遍历结果是：

A.3, 1, 5, 6, 13, 11
B.3, 1, 6, 13, 11, 5
C.1, 3, 11, 6, 13, 5
D.1, 3, 5, 6, 13, 11

B

2-10.对二叉搜索树进行什么遍历可以得到从小到大的排序序列?

A.前序遍历
B.后序遍历
C.中序遍历
D.层次遍历

C

2-11.若二叉搜索树是有N个结点的完全二叉树，则不正确的说法是：

A.平均查找效率是O(logN)
B.最大值一定在最后一层
C.最小值一定在叶结点上
D.中位值结点在根结点或根的左子树上

B

2-12.已知8个数据元素为（34，76，45，18，26，54，92，65），按照依次插入结点的方法生成一棵二叉搜索树后，最后两层上的结点总数为：

A.1
B.2
C.3
D.4

B

2-13.下列叙述正确的是（）。

A.在任意一棵非空二叉搜索树，删除某结点后又将其插入，则所得二叉搜索树与删除前原二叉搜索树相同。
B.二叉树中除叶结点外, 任一结点X，其左子树根结点的值小于该结点（X）的值；其右子树根结点的值≥该结点（X）的值，则此二叉树一定是二叉搜索树。
C.虽然给出关键字序列的顺序不一样，但依次生成的二叉搜索树却是一样的。
D.在二叉搜索树中插入一个新结点，总是插入到最下层，作为新的叶子结点。

D

编程题

7-1 两个有序序列的中位数

已知有两个等长的非降序序列S1, S2, 设计函数求S1与S2并集的中位数。有序序列A_​0,A₁ ,⋯,A_​N−1的中位数指A_​(N−1)/2的值,即第⌊(N+1)/2⌋个数（A₀为第1个数）。

输入格式：

输入分三行。第一行给出序列的公共长度N（0

输出格式：

在一行中输出两个输入序列的并集序列的中位数。

输入样例1
5
1 3 5 7 9
2 3 4 5 6

输出样例
4

输入样例2
6
-100 -10 1 1 1 1
-50 0 2 3 4 5

输出样例
1

参考代码

#include 

using namespace std;

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    int n, i;
    int a[200001];
	cin>>n;
	for(i = 0; i < 2 * n; i++)
		cin>>a[i];
	sort(a, a + 2 * n);
    cout<<a[n - 1]<<endl;
	return 0;
}

7-2 是否同一棵二叉搜索树

给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树，都得到一样的结果。于是对于输入的各种插入序列，你需要判断它们是否能生成一样的二叉搜索树。

输入格式：

输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L，分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数，作为初始插入序列。最后L行，每行给出N个插入的元素，属于L个需要检查的序列。

简单起见，我们保证每个插入序列都是1到N的一个排列。当读到N为0时，标志输入结束，这组数据不要处理。

输出格式：

对每一组需要检查的序列，如果其生成的二叉搜索树跟对应的初始序列生成的一样，输出“Yes”，否则输出“No”。

输入样例
4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0

输出样例
Yes
No
No

鸣谢青岛大学周强老师补充测试数据！

参考代码

#include 

using namespace std;

struct Node
{
    int v;
    Node *lchild;
    Node *rchild;
};

typedef Node *tree;


void Insert(tree &t, int v)
{
    if(t == NULL)
    {
        t = new Node();
        t -> lchild = NULL;
        t -> rchild = NULL;
        t -> v = v;
    }
    else if(v < t -> v)
        Insert(t -> lchild, v);
    else if(v > t -> v)
        Insert(t -> rchild, v);
}

bool Compare(tree &t1, tree &t2)
{
    if(t1 == NULL && t2 == NULL)
        return true;
    if(!t1 || !t2)
        return false;
    if(t1 -> v != t2 -> v)
        return false;
    if(!Compare(t1 -> lchild, t2 -> lchild) || !Compare(t1 -> rchild, t2 -> rchild))
        return false;
    return true;
}

void Creat(tree &t, int n)
{
    int i;
    t = NULL;
    for(i = 0; i < n; i++)
    {
        int data;
        cin>>data;
        Insert(t, data);
    }
}

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    int n, l, i;
    while(scanf("%d", &n) != EOF && n != 0)
    {
        cin>>l;
        tree t1;
        tree t2;
        Creat(t1, n);
        for(i = 0; i < l; i++)
        {
            Creat(t2, n);
            if(Compare(t1, t2))
                cout<<"Yes"<<endl;
            else
                cout<<"No"<<endl;
        }
    }


}

7-3 是否完全二叉搜索树

将一系列给定数字顺序插入一个初始为空的二叉搜索树（定义为左子树键值大，右子树键值小），你需要判断最后的树是否一棵完全二叉树，并且给出其层序遍历的结果。

输入格式：

输入第一行给出一个不超过20的正整数N；第二行给出N个互不相同的正整数，其间以空格分隔。

输出格式：

将输入的N个正整数顺序插入一个初始为空的二叉搜索树。在第一行中输出结果树的层序遍历结果，数字间以1个空格分隔，行的首尾不得有多余空格。第二行输出YES，如果该树是完全二叉树；否则输出NO。

输入样例1
9
38 45 42 24 58 30 67 12 51

输出样例1
38 45 24 58 42 30 12 67 51
YES

输入样例2
8
38 24 12 45 58 67 42 51

输出样例2
38 45 24 58 42 12 67 51
NO

参考代码

#include 

using namespace std;

struct Node
{
    int v;
    Node *lchild;
    Node *rchild;
};

typedef Node *tree;
tree NULLtree;

void Insert(tree &t, int v)
{
    if(t == NULLtree)
    {
        t = new Node();
        t -> lchild = NULLtree;
        t -> rchild = NULLtree;
        t -> v = v;
    }
    else if(v > t -> v)
        Insert(t -> lchild, v);
    else if(v < t -> v)
        Insert(t -> rchild, v);
}


void Creat(tree &t, int n)
{
    int i;
    t = NULLtree;
    for(i = 0; i < n; i++)
    {
        int data;
        cin>>data;
        Insert(t, data);
    }
}

bool Level(tree &t, vector<int> &a)
{
    queue<tree> q;
    q.push(t);
    int flag = 0;
    while(!q.empty())
    {
        tree t2 = q.front();
        q.pop();
        if(t2 != NULLtree)
        {
            if(flag > 0)
                flag = -1;
            a.push_back(t2 -> v);
            if(t2 -> lchild)
                q.push(t2 -> lchild);
            else
                q.push(NULLtree);
            if(t2 -> rchild)
                q.push(t2 -> rchild);
            else
                q.push(NULLtree);
        }
        else
        {
            if(flag >= 0)
                flag++;
        }

    }
    if(flag == -1)
        return true;
    else
        return false;
}

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    int n, l, i;
    NULLtree = new Node();
    NULLtree -> lchild = NULL;
    NULLtree -> rchild = NULL;
    NULLtree -> v = -1;
    while(scanf("%d", &n) != EOF && n != 0)
    {
        tree t;
        Creat(t, n);
        vector<int> a;
        bool flag = Level(t, a);
        cout<<a[0];

        for(i = 1; i < a.size(); i++)
        {
            cout<<" "<<a[i];
        }
        cout<<endl;
        if(!flag)
            cout<<"YES"<<endl;
        else
            cout<<"NO"<<endl;
    }
}