深度学习网络篇——ResNet

ResNet

作者：Kaiming He ，Xiangyu Zhang ，Shaoqing Ren ，Jian Sun

研究机构：Microsoft Research

---

About Kaiming He

2003年广东省理科高考状元，清华基础科学班，香港中文大学攻读研究生，微软亚研院实习，现在FAIR工作

主要文献:

• ResNet，Faster-RCNN（Shaoqing Ren一作）, Single Image去雾，PReLU（自学习Relu，分类性能第一次超越人类level), SPP-Net(ECCV2014),
• Identity Mappings in Deep Residual Networks（2016ECCV，ResNet的后续原理分析及改进）
• Focal Loss（三作),R-FCN（三作）
• Instance-Aware Semantic Segmentation via Multi-task Network Cascades（2016CVPR，2015MSCOCO语义分割冠军）,Mask-RCNN
• Aggregated Residual Transformations for Deep Neural Networks（2017CVPR，ResNeXt）
• 等等等等…还有很多的精彩成果这里不再提及。有兴趣可以参考何凯明主页：http://kaiminghe.com

---

下面我们正式开始聊论文，啊哈哈哈哈哈~

1. Background

• Forward：from shallow to deep

  • Alexnet的出现带火了深度学习，其最重要的特点为通过数据驱动让模型自动学习特征，省去了人工寻找特征的步骤。但不同的模型也找出不同质量的特征，特征的质量直接影响到分类结果的准确度，表达能力更强的特征也给模型带来更强的分类能力。因此，深度网络通过数据学习到表达能力更强的特征。
  • 特征也可以根据复杂度和表示能力粗略的分为高中低三种种类，理论上讲越复杂的特征有越强的表征能力。在深度网络中，各个特征会不断的经过线性非线性的综合计算，越深的网络输出表示能力越强的特征。所以，网络的深度对于学习表达能力更强的特征至关重要，这一问题在VGGNet中得到很好体现。
  • 深度模型中，每层的输出特征图的尺寸大都随着网络深度而变化，主要是高和宽越来越小，输出特征图的深度随着网络层数的深度而增加，这一设计符合Inception v3 paper中的原则，从另一方面讲，高和宽的减小有助于减小计算量，而特征图深度的增加则使每层输出中可用特征数量的增多。

  以上所提论文皆在我们的博客中逐个分析过，没看过的朋友可以参考博客中过往文章PRIS-SCMonkey

• Backward：the problem caused by increasing depth

  • 增加深度带来的首个问题就是梯度爆炸/消散的问题，这是由于随着层数的增多，在网络中反向传播的梯度会随着连乘变得不稳定，变得特别大或者特别小。这其中经常出现的是梯度消散的问题。

  • 为了克服梯度消散也想出了许多的解决办法，如使用BatchNorm，将激活函数换为ReLu，使用Xaiver初始化等，可以说梯度消散已经得到了很好的解决

  • 增加深度的另一个问题就是网络的degradation问题，即随着深度的增加，网络的性能会越来越差，直接体现为在训练集上的准确率会下降，残差网络文章解决的就是这个问题，而且在这个问题解决之后，网络的深度上升了好几个量级。

• Degradation of deep network

  With network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly. Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher training error.

• 上图是论文中随着网络深度的增加网络在CIFAR10-数据集上分类的训练集的错误率，可以看到如果我们直接堆叠卷积层，随着层数的增多，错误率有明显上升的趋势，其中最深的56层网络得到了最差的准确率，我们在VGG网络上验证了一下，对于CIFAR-10数据集在18层的VGG网络上耗费5分钟时间在网络训练充分的情况下得到了80%正确率，而34层的VGG模型花费8分钟得到了72%正确率，网络衰退问题确实存在。

• 训练集错误率的下降说明degredation的问题并不是过拟合所造成，具体原因论文中也只是说留待继续研究，在作者的另一篇论文《Identity Mappings in Deep Residual Networks》中证明了degradation的产生是由于优化性能不好，这说明越深的网络反向梯度越难传导。

2.Deep Residual Networks

• From 10 to 100 layers

  • 我们可以设想一下，当我们直接对网络进行简单的堆叠到特别长，网络内部的特征在其中某一层已经达到了最佳的情况，这时候剩下层应该不对改特征做任何改变，自动学成恒等映射(identity mapping) 的形式。也就是说，对一个特别深的深度网络而言，该网络的浅层形式的解空间应该是这个深度网络解空间的子集，换句话说，相对于浅层网络更深的网络至少不会有更差的效果，但是因为网络degradation的问题，这并不成立。

  • 那么，我们退而求其次，已知有网络degradation的情况下，不求加深度能提高准确性，能不能至少让深度网络实现和浅层网络一样的性能，即让深度网络后面的层至少实现恒等映射的作用，根据这个想法，作者提出了residual模块来帮助网络实现恒等映射。

    Let us consider a shallower architecture and its deeper counterpart that adds more layers onto it. There exists a solution to the deeper model by construction: the layers are copied from the learned shallower model, and the added layers are identity mapping. The existence of this constructed solution indicates that a deeper model should produce no higher training error than its shallower counterpart.

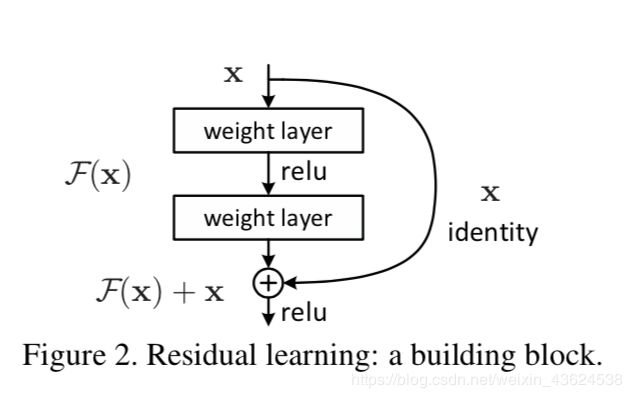
• Residual Module

Instead of hoping each stack of layers directly fits a desired underlying mapping, we explicitly let these layers fit a residual mapping. The original mapping is recast into F(x)+x. We hypothesize that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping. To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.

• 根据上图，copy一个浅层网络的输出加给深层的输出，这样当网络特征达到optimal的时候更深层恒等映射的任务就从原来堆叠的层中释放到新建的这个恒等映射关系中，而原来层中的任务就从恒等映射转为全0。
• $F(x)=H(x)-x$，x为浅层的输出，$H(x)$为深层的输出,$F(x)$为夹在二者中间的的两层代表的变换，当浅层的x代表的特征已经足够成熟，如果任何对于特征$x$的改变都会让loss变大的话，$F(x)$会自动趋向于学习成为0，$x$则从恒等映射的路径继续传递。这样就在不增加计算成本的情况下实现了一开始的目的：在前向过程中，当浅层的输出已经足够成熟（optimal），让深层网络后面的层能够实现恒等映射的作用。

那么从另一个角度看，在反向传播中，residual模块会起到什么样的作用呢？

• residual模块将输出分成$F(x)+x$两部分，其中F依然是$x$的函数，也就是说F实际上是对于$x$的补充，是对于$x$的fun-tuning，这样就把任务从根据$x$映射成一个新的$y$转为了根据$x$求$x$和$y$之间的差距，这明显是一个相对更加简单的任务，论文是这么写的，到底怎么简单的，我们来分析一下。

• 举个例子，假设不加residual模块的输出为$h(x)$。$x=10,h(x)=11$,$h$简化为线性运算$W_h$,$W_h$明显为1.1，加了redidual模块后，$F(x)=1$,$H(x)=F(x)+x=11$，F也简化为线性运算,对应的$W_F$为0.1。当标签中的真实值为12，反向传播的损失为1，而对于F中的参数和h中参数回传的损失实际上是一样大的而且梯度都是x的值，但是对于F的参数就从0.1到0.2，而h的参数是从1.1到1.2，因此redidual模块会明显减小模块中参数的值从而让网络中的参数对反向传导的损失值有更敏感的响应能力，虽然根本上没有解决回传的损失小得问题，但是却让参数减小，相对而言增加了回传损失的效果，也产生了一定的正则化作用。

• 其次，因为前向过程中有恒等映射的支路存在，因此在反向传播过程中梯度的传导也多了更简便的路径，仅仅经过一个relu就可以把梯度传达给上一个模块。

• 所谓反向传播就是网络输出一个值，然后与真实值做比较的到一个误差损失，同时将这个损失做差改变参数，返回的损失大小取决于原来的损失和梯度，既然目的是为了改变参数，而问题是改变参数的力度过小，则可以减小参数的值，使损失对参数改变的力度相对更大。

• 因此残差模块最重要的作用就是改变了前向和后向信息传递的方式从而很大程度上促进了网络的优化。

• 利用Inceptionv3提出的四个准则我们再用一下以改进residual模块，利用准则3，再空间聚合之前先进行降维不会发生信息丢失，所以这里也采用了同样的方法，加入1*1的卷积核用来增加非线性和减小输出的深度以减小计算成本。就得到了成为bottleneck的residual模块形式。上图左为basic形式，右为bottleneck的形式。

• 综上所述，shortcut模块会在前向过程中帮助网络中的特征进行恒等映射，在反向过程中帮助传导梯度，让更深的模型能够成功训练。

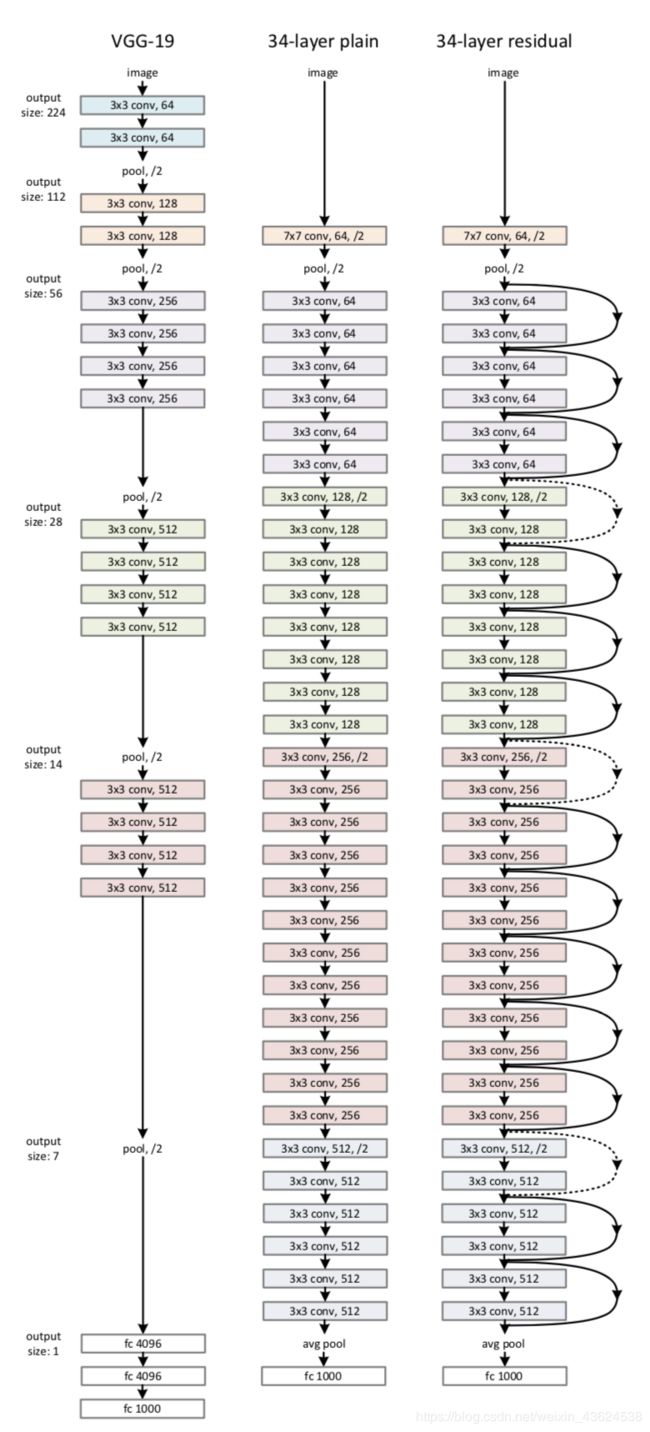
左边为基础的VGG，中间为基于VGG作出的扩增至34层的普通网络，右边为34层的残差网络，不同的是每隔两层就会有一个residual模块。

• Experientment about ResNet-100

  • 以往模型大多在ImageNet上作测试，所以这里只给出在ImageNet上的成绩，论文还在CIFAR-10/100上做了测试。

    resnet具体代码见：ResNet

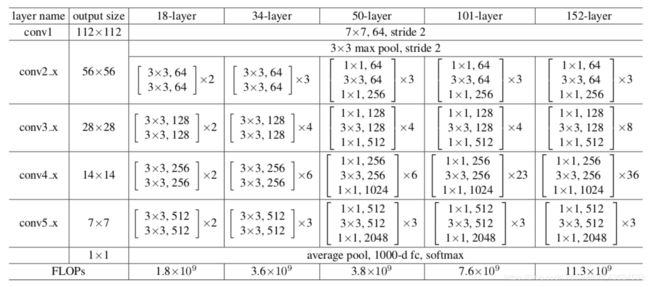
网络配置

• 需要注意的一点是对于block和block之间的特征大小不同时，因为是在F内部发生变化，x也需要随之变化才能对应相加，论文中采用的调整方法是采用0填充来拟补深度，但是如何缩小特征尺寸没有说，而且官网的复现方式都是直接用一个1*1的卷积核来操作这一步，理论上讲会破坏恒等映射。

• result：
  

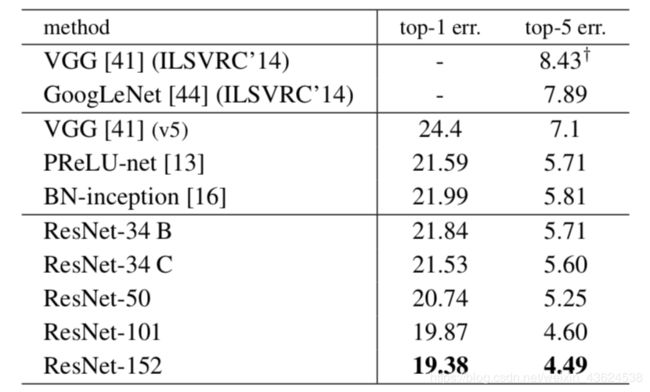
  单个模型在ImageNet的精度

• 152层的ResNet相比于其他网络有提高了一些精度，并且ResNet的参数量为1.1千万，VGG16参数数量为1.53千万，可见虽然ResNet深度增加了近十倍，但是参数量因为使用bottleneck模块反而更少。

• From 100 to 1000 layers

  • 接着上面的ResNet想，可以说ResNet的成功是借助于residual模块的引入很好的解决了网络degradation的问题，从而提高了网络深度，得到了表达能力更强的特征，有了更高的准确度。那么我们还能不能加深一些呢？100层可以，1000层呢？
  • 答案是不可以，至少目前的残差模型是不行的，因为目前的残差块在加和之后会经过一个relu，这增加的操作虽然在100层中不会有很大的影响，但是在1000层的超深网络里面还是会阻碍整个网络的前向反响传播，我们需要接着改进。

• Improve residual module

  $$y_l=h(x_l)+F(x_l,W_l)\text{\hspace{1em}(1)}$$

  $$x_{l+1}=f(y_l)\text{\hspace{1em}(2)}$$

  • 上式是残差模块中的基本形式，$h(x)$是恒等映射，$F$是网络中的变化，$f(x)$是对于叠加之后值的变换，在原始残差模块中是relu，网络通过学习其中的$F$的参数来减小loss值。我们希望能够为整个网络信息的传播构造一个流畅的通道，这就要求$h$和$f$都必须是恒等映射,即：

  • 如果$f$也是恒等映射的话，那么$x_{l+1}\equiv y$,我们就可以把公式(2)并入到公式(1)，得到：
    $$x_{l+1}=x_l+F(x_l,W_l).\text{\hspace{1em}(3)}$$
    其中$x_l$又可以拆分为上一模块的输出和l层残差模块的加和，因此循环递归得到以下公式：

    $x_{l+2}=x_{l+1}+F(x_{l+1},W_{l+1})=x_l+F(x_l,W_l)+F(x_{l+1},W_{l+1})$,不停的循环下去得到通式：
    $$x_L=x_l+\sum _{i=l}^{L-1}F(x_i,W_i)\text{\hspace{1em}(4)}$$
    可以看到，对于L层的输出而言，可以看作任何一个L层之前的l层的输出$x_l$和中间残差块的输出的叠加（注意中间残差块的输入也是随着i变化的，因此每个残差块内部也都有l层输出$x_l$的作用），因此整个网络是residual fashion的，可以把任何一层和该层之前的任何一层看成残差模块，这样就保证了整个网络的前向传播的畅通。

    改进后网络的反向传播公式如下：
    $$\frac{\partial l}{\partial x_l}=\frac{\partial l}{\partial x_L}\frac{\partial x_L}{\partial x_l}=\frac{\partial l}{\partial x_L}(1+\frac{\partial }{\partial x_l}\sum _{i=l}^{L-1}F(x_i,W_i))\text{\hspace{1em}(5)}$$

  • 可以看到，对于任何一层的x的梯度由两部分组成，其中一部分直接就由L层不加任何衰减和改变的直接传导l层，这保证了梯度传播的有效性,另一部分也由链式法则的累乘变为了累加，这样有更好的稳定性。

• The importance of identity mapping

  • 我们从另外一个角度来看identity mapping在$h$和$f$中的重要性，首先来分析$h$，如果$h$不是恒等映射，而是网络中一些其他很常见的操作如卷积，我们简化卷积操作为简单的给$h$乘上一个系数 $\lambda$,这样原来的前向传播公式(4)就变成了:

  $$x_L=(\prod _{i=l}^{L-1}{\lambda }_i)x_l+\sum _{i=l}^{L-1}F(x_i,W_i)\text{\hspace{1em}(6)}$$

  反向传播为：
  $$\frac{\partial l}{\partial x_l}=\frac{\partial }{\partial x_L}((\prod _{i=l}^{L-1}{\lambda }_i)+\frac{\partial }{\partial x_l}\sum _{i=l}^{L-1}F(x_i,W_i)).\text{\hspace{1em}(7)}$$

  • 当$\lambda$大于1，传播回来的梯度因为累乘会变得很大，会产生梯度爆炸的效应，让网络更难训练，当$\lambda$小于1，从shortcut传播回的梯度会趋近于0，这样网络就要回到最初的起点从参数层传播，我们知道对于很深的网络而言这种方式是很难传播的。因此对于h设为恒等映射对于深度网络的训练最有效。

残差模块的几种可能的设置

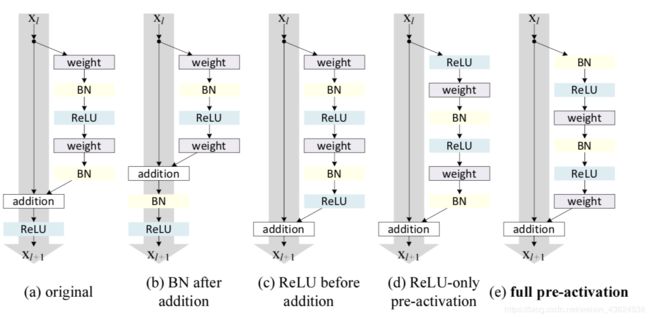
• 然后我们来分析$f$为恒等映射的重要性和相关设置。在原始残差模块中，$F$和h相加之后经过一个relu再输到下一个block，我们有那么几种做法来去掉relu操作来保持f的identity mapping，第一个就是把relu放回参数层F中，如上图中的©，但这样会让F中拟合的对于x的残差只有正值，会大大减小残差的表示性。

• 文章提出了一种叫pre-activation的方式，即把BN和relu放在卷积的前面，这样就可以保证F中所有的操作都在和x相加之前完成，并且不会对残差产生限制，上图中的(e)。实际上把激活层（relu+BN）放在卷积的前面的操作在VGG等网络中不会产生不同的影响，但是在残差网络中就可以保证输入和输出加和之后在输入下一层之前没有别的操作，让整个信息的前向后向流动没有任何阻碍，从而让模型的优化更加简单和方便。

• 对于(d)这种只把relu提前的操作也会产生问题，当F中经过最后一个BN后，还要经过一个和x相加的运算，本来BN就是为了给数据一个固定的分布，一旦经过别的操作就会改变数据的分布，会削减BN的作用。在原版本的resnet中就是这么使用的BN，所以这种pre-activation的方式也增加了残差模块的正则化作用。

• Experiment about ResNet-1000

100层的不同残差网络比较

• 和原始152层残差模型相比，改进后的残差模型在精度上并没有很大的提升，这说明原始的残差模块在152层的网络上已经有足够好的性能。（这也是为什么152层的模型代码大多依然保持最开始的残差模块）

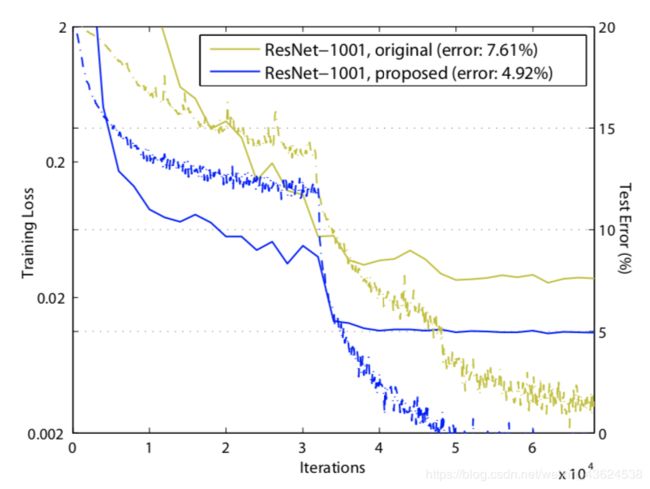
1000层不同残差网络比较

• 相比于原始1000层残差模型，改进残差块后有了很大的精度提升，究其原因是改进后的残差模块提供了更加有效的反向传播方式，让梯度更有效的传导到模型任何一层，让训练更加容易，从而激发了更多深度模型的性能。

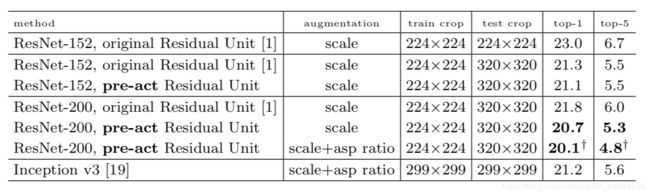
各模型之间的横向比较（†代表mini-batch 为64）

• 1000层的残差网络获得了最好的性能，值的注意的是这所有精度提升都是出自于深度的增加。

• 1000层的残差网络和100层的网络之间的计算复杂度基本是线性的，因此从时间和算力的角度而言还是100层的网络更加实用，但是改进后的残差模块证明了1000层的网络的可实现性，实际上现在各大厂每次开会都要拿超深的网络出来吓人，原理就是这个模块。

• Alexnet出现之后，图像的问题基本都由深度学习来解决，残差网络出现之后，之后的模型大都是残差模型的变体。我们重新审视一下ResNet，为了增加图像分类的精度很重要的一个方面就是增加网络学习特征的质量，而特征的表达能力与网络的深度有很大的关系，越深的网络理论上有表征能力更强的特征，ResNet解决的就是更深的网络这个问题，那么，我们有没有什么其他不是靠深度的办法来增加特征的表征能力呢？如果有的话结合上ResNet的深度，会不会产生很好的效果呢？

3.other residual module

• More wild residual

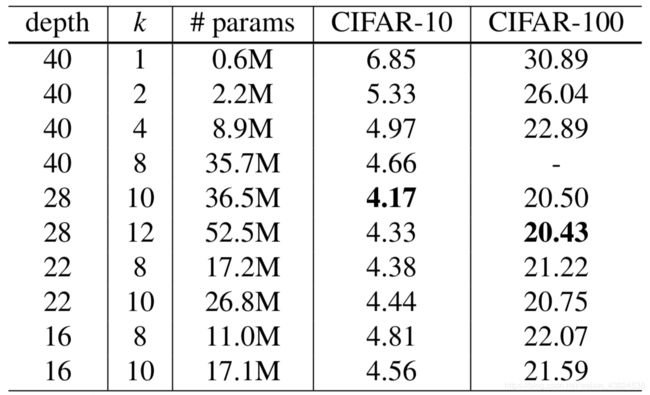
  • 残差网络主要是研究深度对于网络的性能影响，并且在增加深度的同时为了减少计算量尽量让模型变瘦，用了bottleneck模块等技巧让每层的卷积核数量尽量少，但模型的深度到达一定程度之后，参数尽管大幅上升，但是不能带来相对应的性能的大幅提升，于是《Wide Residual Networks》这篇论文分析研究了宽度（每层卷积核数量）对于残差网络的影响，并用16层的改进残差网络就达到了1000层残差网络的性能，尽管提高了参数的数量，却需要更短的训练时间。

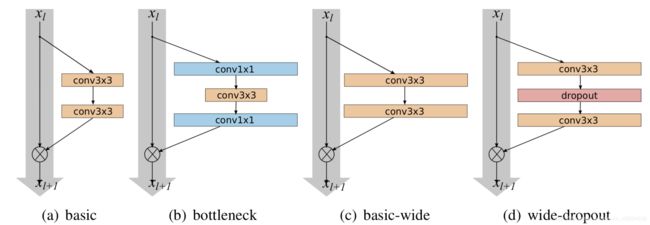
上图是文章中实验的4种残差模型，(d)是文章中提出，可以看到相比于基础模块在中间加上了dropout层，这是因为增加了宽度后参数的数量会显著增加，为了防止过拟合使用了卷积层中的dropout，并取得了相比于不用dropout更好的效果。

• 文章通过实验发现每个残差内部由两个33卷积层组成可以有最好的效果，上图是改进后模型的基本架构，沿用了原是残差模型中model–>block—>residual的形式，唯一不同的知识多了一个k的参数，代表了原始模块中卷积核数量的k倍，B（3，3）代表每一个残差模块内由两个33的卷积层组成。

上图是不同宽度的模型之间纵向比较，同深度下，随着宽度增加，准确率增加。深度为22层，宽度为原始8倍的模型比深度为40层的同宽的模型准确率还要高。我们可以得到如下结论

1.增大宽度可以增加各种深度的残差模型的性能

2.只要参数的数量可以接受，宽度和深度的增加就可以使性能提升。

3.在相同的参数数量下，更深的模型并不比更宽的模型有更好的性能。

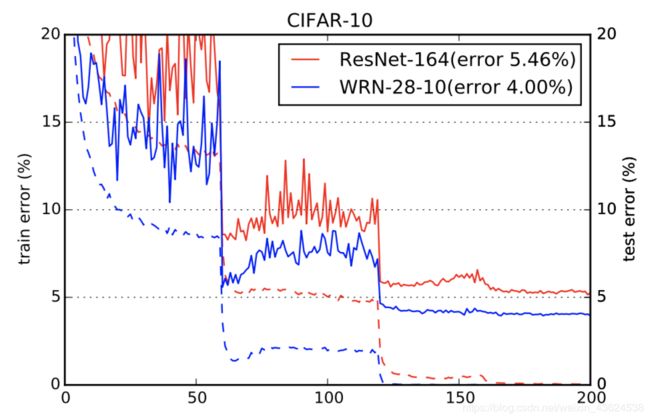
上图是164层原始残差网络和28层十倍宽度残差网络的比较，可以看到，改进后的宽网络有更低的错误率。这也证明了残差模型的性能提升主要在残差模块的残差部分上，而不是恒等映射部分。

• Inception v4

  • GoogLeNet的Inception模块是很好的增加单层特征表达性能的方式，因此Inception和Residual二者就很好的结合了，具体细节在《Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning》中。主要思想为利用残差模块来帮助提升深度和加速训练，同时保持Inception的多分支卷积的形式来帮助增加前向过程的特征表达能力。

  • 值的注意的是作者在Inceptionv4论文中共提出了3个新的网络：Inceptionv4，Inception-ResNetv1,Inception_ResNetv2，并拿这三个网络加上Inceptionv3一起进行比较。

    具体形式如下：

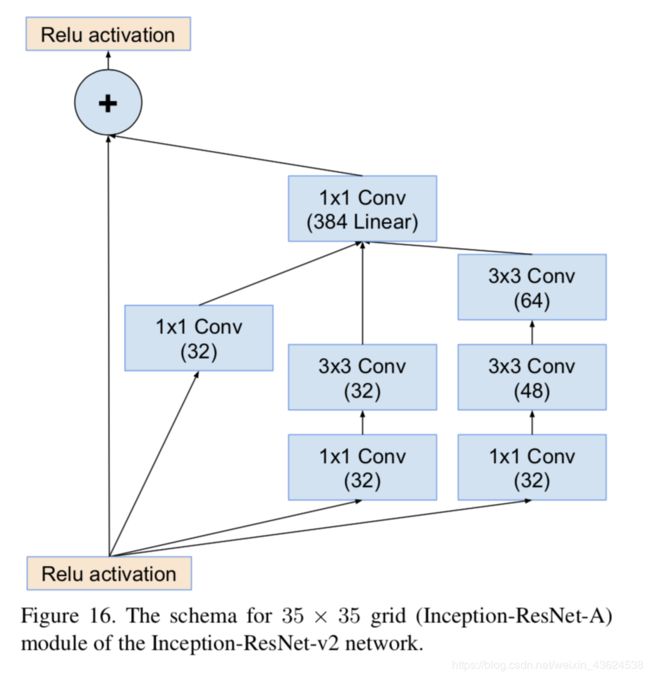
• 如上面的图片所示，改进主要有两点。1：将ressidual模块加入inception，2：将各分支的输出通过聚合后通过同一个1*1的卷积层来进行通道的扩增。

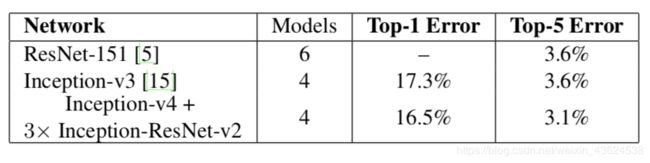
从上图可以看出，加了Residual模块的模型训练速度明显比正常的Inception模型快一些，而且也有稍微高一些的准确率。

最后集合模型的Top-5准确率达到了3.1%

• ResneXt

  • wide residual研究了宽度对于残差网络的重要性，并提出了网络性能提升的关键在于残差模块，而不是shortcut，ResNeXt基于wide residual和inception，提出了另一个方向，即将残差模块中的所有通道分组进行汇合操作会有更好的效果，同时也给inception提出了一个抽象化的表示方式。

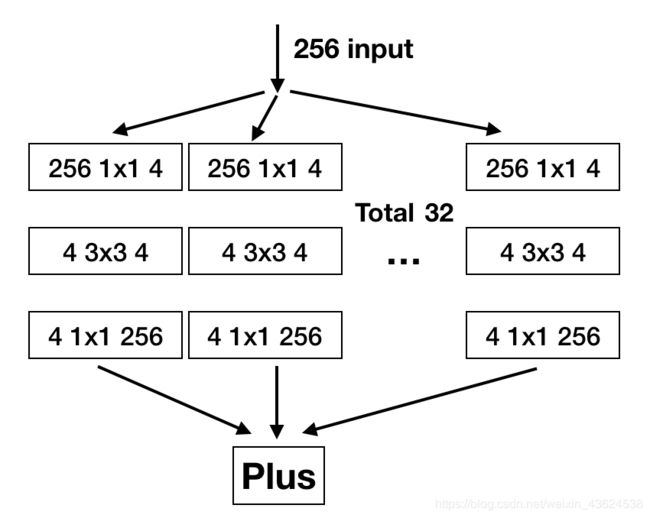
  • 简化的inception

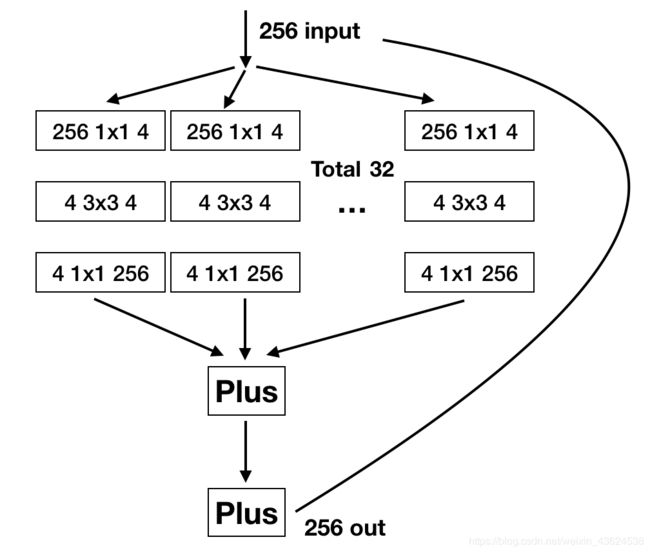
将Inception的不同尺寸的卷积核和池化等归一化为3*3的卷积核，并且每个分支都用1 * 1的卷积核去扩展通道后相加就得到了上面的结构，再这个基础上加上shortcut就得到了ResneXt模块：

1.相对于Inception-Resnet，ResNeXt的每个分支都是相同的结构，相对于Inception，网络架构更加简洁。

2.Inception-Resnet中的先各分支输出concat然后1 * 1卷积变换深度的方式被先变换通道数后单位加的形式替代。

3.因为每个分支的相同结构，可以提出除了深度和宽度之外的第三维度cardinality，即分支的数量

• 以上的结构实际上贴合了神经网络的拟合方式，一个二层的神经网络表达形式为：$y={\sum }_{i=0}^C{f}_i(x)$,每个$f_i$代表对输入x的变换，C代表对于输入进行变换的数量，其中$f$在全连接中为输入和参数向量的点积，RexNeXt将点积改为复杂的三层卷积运算，最后也是单位加。

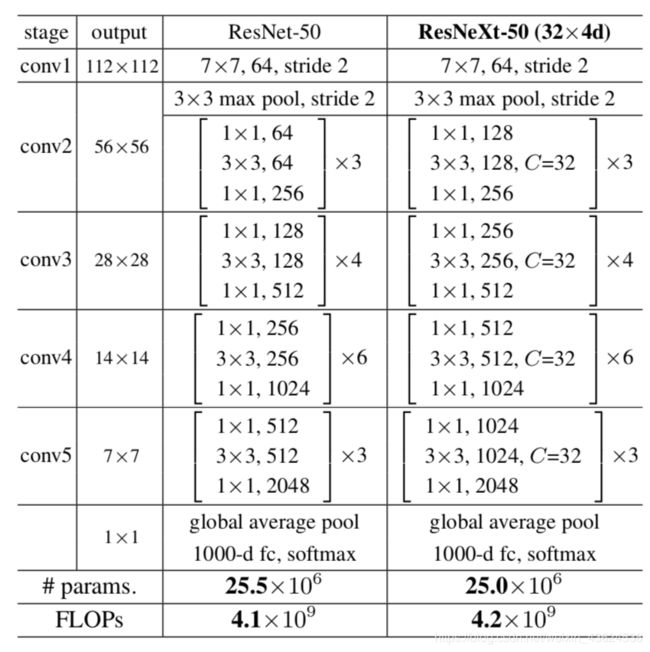
上图是ResNeXt的配置图，可以类比Wide Residual的配置图，二者一个是改变了卷积核的倍数，一个增加了分组，但都是在残差模块做工作。

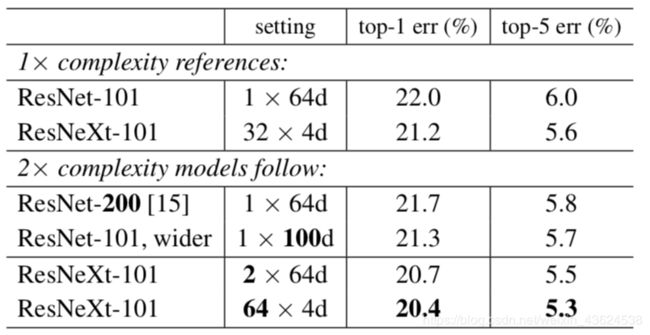
可以看到，相对于100层的残差网络，用深度，宽度，和cardinality三种方式增大了两倍的复杂度，相同复杂度下，分组更多即C更大的模型性能更好，这说明cardinality是一个比深度和宽度更加有效的维度。

4.Final

• 第三部分只是简单介绍几个残差结构的可能变体，逻辑和内容不能保证完善，有兴趣的同学可以学习原始论文。

• 我们分析了残差模型的基本构造以及改进方式，并在最后介绍了几个基于残差模型的变体,本文供实验室内部交流学习使用，能力有限精力有限，对于错误和不足的地方，希望大家多多包涵并批评指正。

最后，目前这是我们分享的最长的网络和最长的文章啦（因为ResNet的伙伴们真的是太多了…），感谢小伙伴们一直以来的支持，下周是DenseNet哦！大家下周见~么么啾！！！！