简介:
割边和割点的定义仅限于无向图中。我们可以通过定义以蛮力方式求解出无向图的所有割点和割边,但这样的求解方式效率低。Tarjan提出了一种快速求解的方式,通过一次DFS就求解出图中所有的割点和割边。
欢迎探讨,如有错误敬请指正
如需转载,请注明出处 http://www.cnblogs.com/nullzx/
1. 割点与桥(割边)的定义
在无向图中才有割边和割点的定义
割点:无向连通图中,去掉一个顶点及和它相邻的所有边,图中的连通分量数增加,则该顶点称为割点。
桥(割边):无向联通图中,去掉一条边,图中的连通分量数增加,则这条边,称为桥或者割边。
割点与桥(割边)的关系:
1)有割点不一定有桥,有桥一定存在割点
2)桥一定是割点依附的边。
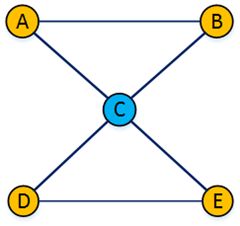
下图中顶点C为割点,但和C相连的边都不是桥。
2. 暴力解决办法解决求解割点集和割边集
暴力法的原理就是通过定义求解割点和割边。在图中去掉某个顶点,然后进行DFS遍历,如果连通分量增加,那么该顶点就是割点。如果在图中去掉某条边,然后进行DFS遍历,如果连通分量增加,那么该边就是割边。对每个顶点或者每个边进行一次上述操作,就可以求出这个图的所有割点和割边,我们称之为这个图的割点集和割边集。
在具体的代码实现中,并不需要真正删除该顶点和删除依附于该顶点所有边。对于割点,我们只需要在DFS前,将该顶点对应是否已访问的标记置为ture,然后从其它顶点为根进行DFS即可。对于割边,我们只需要禁止从这条边进行DFS后,如果联通分量增加了,那么这条边就是割边。
3. Tarjan算法的原理
判断一个顶点是不是割点除了从定义,还可以从DFS(深度优先遍历)的角度出发。我们先通过DFS定义两个概念。
假设DFS中我们从顶点U访问到了顶点V(此时顶点V还未被访问过),那么我们称顶点U为顶点V的父顶点,V为U的孩子顶点。在顶点U之前被访问过的顶点,我们就称之为U的祖先顶点。
显然如果顶点U的所有孩子顶点可以不通过父顶点U而访问到U的祖先顶点,那么说明此时去掉顶点U不影响图的连通性,U就不是割点。相反,如果顶点U至少存在一个孩子顶点,必须通过父顶点U才能访问到U的祖先顶点,那么去掉顶点U后,顶点U的祖先顶点和孩子顶点就不连通了,说明U是一个割点。
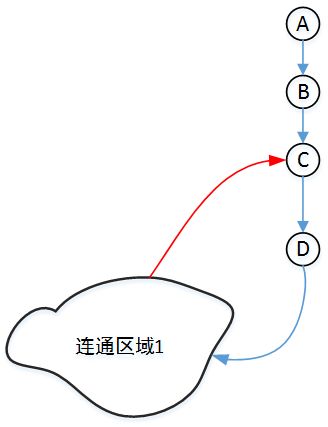
上图中的箭头表示DFS访问的顺序(而不表示有向图),对于顶点D而言,D的孩子顶点可以通过连通区域1红色的边回到D的祖先顶点C(此时C已被访问过),所以此时D不是割点。
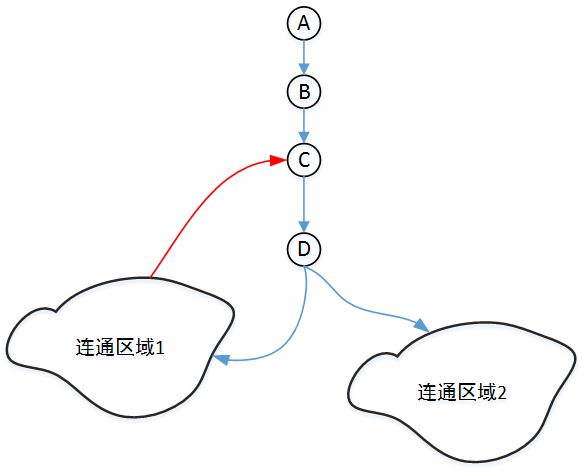
上图中的连通区域2中的顶点,必须通过D才能访问到D的祖先顶点,所以说此时D为割点。再次强调一遍,箭头仅仅表示DFS的访问顺序,而不是表示该图是有向图。
这里我们还需要考虑一个特殊情况,就是DFS的根顶点(一般情况下是编号为0的顶点),因为根顶点没有祖先顶点。其实根顶点是不是割点也很好判断,如果从根顶点出发,一次DFS就能访问到所有的顶点,那么根顶点就不是割点。反之,如果回溯到根顶点后,还有未访问过的顶点,需要在邻接顶点上再次进行DFS,根顶点就是割点。
4. Tarjan算法的实现细节
在具体实现Tarjan算法上,我们需要在DFS(深度优先遍历)中,额外定义三个数组dfn[],low[],parent[]
4.1 dfn数组
dnf数组的下标表示顶点的编号,数组中的值表示该顶点在DFS中的遍历顺序(或者说时间戳),每访问到一个未访问过的顶点,访问顺序的值(时间戳)就增加1。子顶点的dfn值一定比父顶点的dfn值大(但不一定恰好大1,比如父顶点有两个及两个以上分支的情况)。在访问一个顶点后,它的dfn的值就确定下来了,不会再改变。
4.2 low数组
low数组的下标表示顶点的编号,数组中的值表示DFS中该顶点不通过父顶点能访问到的祖先顶点中最小的顺序值(或者说时间戳)。
每个顶点初始的low值和dfn值应该一样,在DFS中,我们根据情况不断更新low的值。
假设由顶点U访问到顶点V。当从顶点V回溯到顶点U时,
如果
dfn[v] < low[u]
那么
low[u] = dfn[v]
如果顶点U还有它分支,每个分支回溯时都进行上述操作,那么顶点low[u]就表示了不通过顶点U的父节点所能访问到的最早祖先节点。
4.3 parent数组
parent[]:下标表示顶点的编号,数组中的值表示该顶点的父顶点编号,它主要用于更新low值的时候排除父顶点,当然也可以其它的办法实现相同的功能。
4.4 一个具体的例子
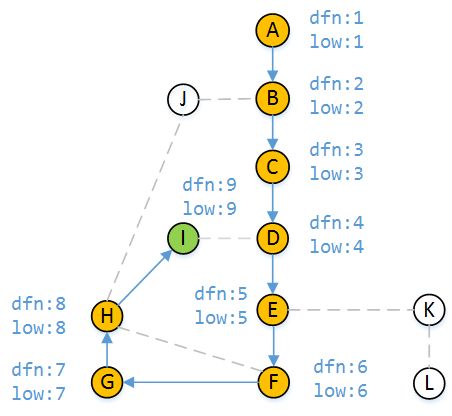
现在我们来看一个例子,模仿程序计算各个顶点的dfn值和low值。下图中蓝色实线箭头表示已访问过的路径,无箭头虚线表示未访问路径。已访问过的顶点用黄色标记,未访问的顶点用白色标记,DFS当前正在处理的顶点用绿色表示。带箭头的蓝色虚线表示DFS回溯时的返回路径。
1)
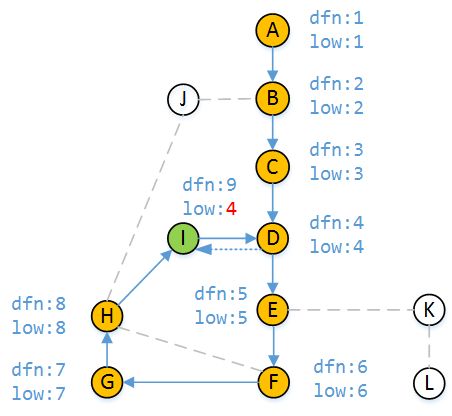
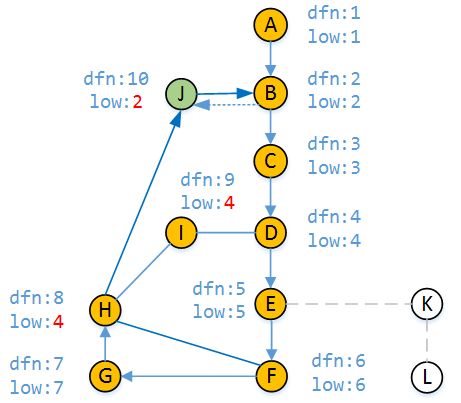
当DFS走到顶点H时,有三个分支,我们假设我们先走H-I,然后走H-F,最后走H-J。从H访问I时,顶点I未被访问过,所以I的dfn和low都为9。根据DFS的遍历顺序,我们应该从顶点I继续访问。
2)
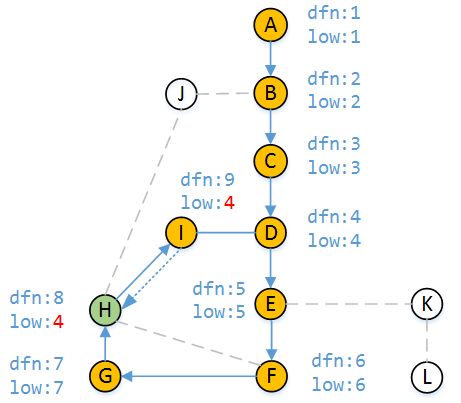
上图表示由顶点I访问顶点D,而此时发现D已被访问,当从D回溯到I时,由于
dfn[D] < dfn[I]
说明D是I的祖先顶点,所以到现在为止,顶点I不经过父顶点H能访问到的小时间戳为4。
3)
根据DFS的原理,我们从顶点I回到顶点H,显然到目前为止顶点H能访问到的最小时间戳也是4(因为我们到现在为止只知道能从H可以通过I访问到D),所以low[H] = 4
4)
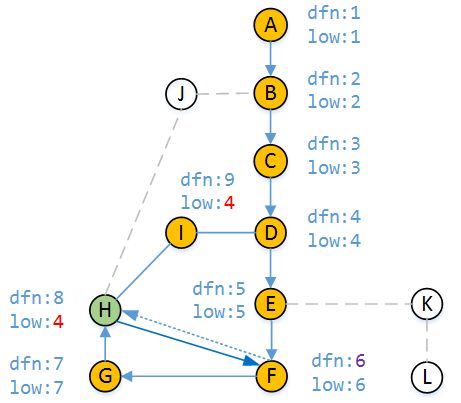
现在我们继续执行DFS,走H-F路径,发现顶点F已被访问且dfn[F] < dfn[H],说明F是H的祖先顶点,但此时顶点H能访问的最早时间戳是4,而F的时间戳是6,依据low值定义low[H]仍然为4。
5)
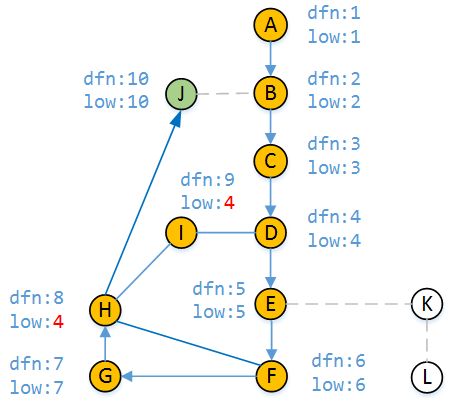
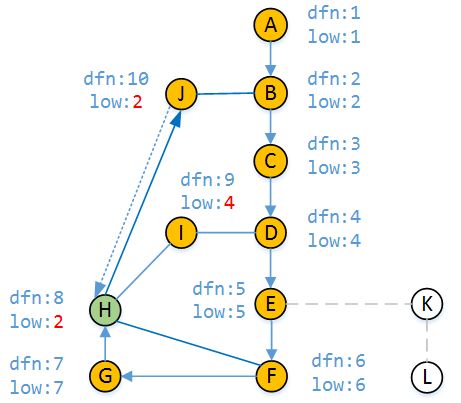
最后我们走H-J路径,顶点J未被访问过所以 dfn[J] = 10 low[J] = 10
6)
同理,由DFS访问顶点B,dfn[J] > dfn[B],B为祖先顶点,顶点J不经过父顶点H能访问到的最早时间戳就是dfn[B],即low[J] = 2
7)
我们从顶点J回溯到顶点H,显然到目前为止顶点H能访问到的最早时间戳就更新为2(因为我们到现在为止知道了能从H访问到J),所以low[H] = 2
8)
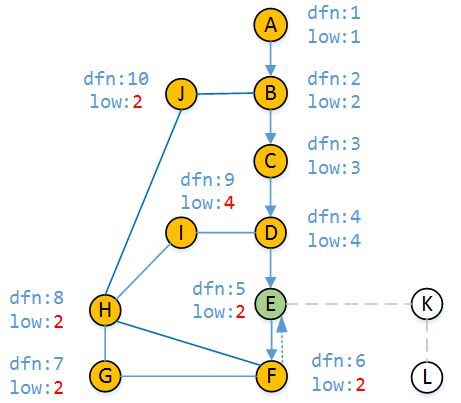
根据DFS原理,我们从H回退到顶点E(H回退到G,G回退到F,F回退到E的过程省略),所经过的顶点都会更新low值,因为这些顶点不用通过自己的父顶点就可以和顶点B相连。当回溯到顶点E时,还有未访问过的顶点,那么继续进行E-K分支的DFS。
9)
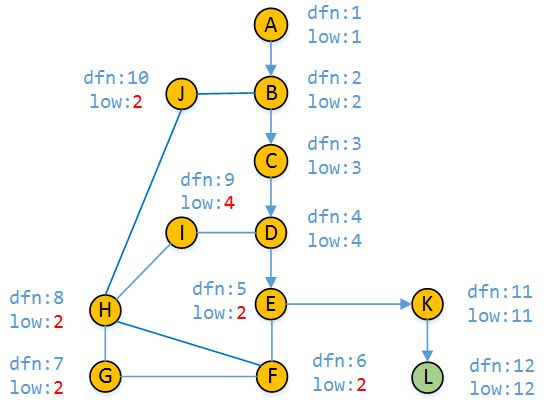
从E-K分支访问到顶点L时,顶点k和L的的dfn值和low值如图上图所示
10)
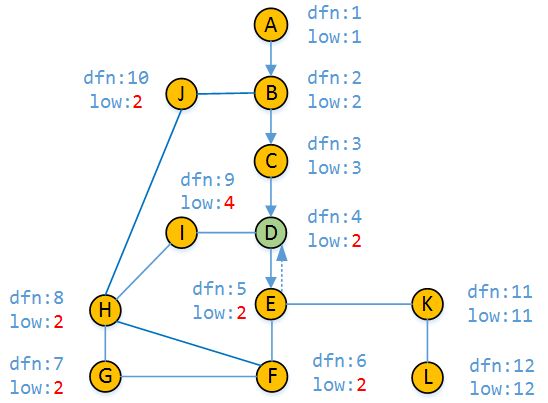
接着我们继续回溯到了顶点D(中间过程有所省略),并更新low[D]
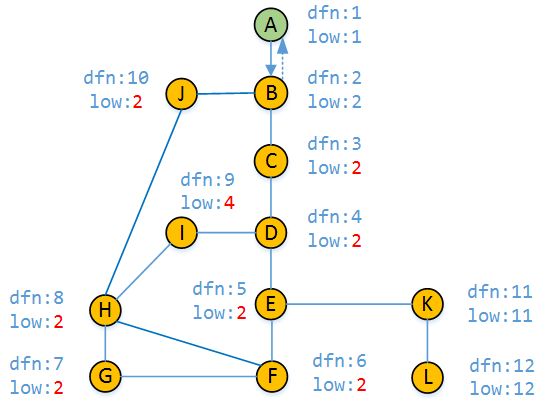
11)
最后,按照DFS的原理,我们回退到顶点A,并且求出来了每个顶点的dfn值和low值。
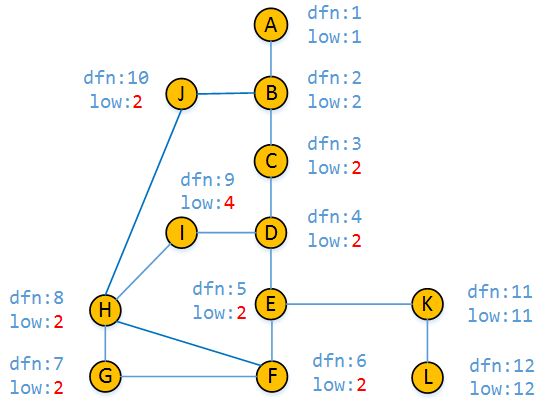
4.5 割点及桥的判定方法
割点:判断顶点U是否为割点,用U顶点的dnf值和它的所有的孩子顶点的low值进行比较,如果存在至少一个孩子顶点V满足low[v] >= dnf[u],就说明顶点V访问顶点U的祖先顶点,必须通过顶点U,而不存在顶点V到顶点U祖先顶点的其它路径,所以顶点U就是一个割点。对于没有孩子顶点的顶点,显然不会是割点。
桥(割边):low[v] > dnf[u] 就说明V-U是桥
需要说明的是,Tarjan算法从图的任意顶点进行DFS都可以得出割点集和割边集。
从上图的结果中我们可以看出,顶点B,顶点E和顶点K为割点,A-B以及E-K和K-L为割边。
5. 代码实现
package datastruct;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileNotFoundException;
import java.io.FileReader;
import java.io.PrintWriter;
import java.io.Reader;
import java.io.StringWriter;
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;
public class CutVerEdge {
/*用于标记已访问过的顶点*/
private boolean[] marked;
/*三个数组的作用不再解释*/
private int[] low;
private int[] dfn;
private int[] parent;
/*用于标记是否是割点*/
private boolean[] isCutVer;
/*存储割点集的容器*/
private List listV;
/*存储割边的容器,容器中存储的是数组,每个数组只有两个元素,表示这个边依附的两个顶点*/
private List listE;
private UndirectedGraph ug;
private int visitOrder;/*时间戳变量*/
/*定义图的边*/
public static class Edge{
/*边起始顶点*/
private final int from;
/*边终结顶点*/
private final int to;
public Edge(int from, int to){
this.from = from;
this.to= to;
}
public int from(){
return this.from;
}
public int to(){
return this.to;
}
public String toString(){
return "[" + from + ", " + to +"] ";
}
}
/*定义无向图*/
public static class UndirectedGraph{
private int vtxNum;/*顶点数量*/
private int edgeNum;/*边数量*/
/*临接表*/
private LinkedList[] adj;
/*无向图的构造函数,通过txt文件构造图,无权值*/
@SuppressWarnings("unchecked")
public UndirectedGraph(Reader r){
BufferedReader br = new BufferedReader(r);
Scanner scn = new Scanner(br);
/*图中顶点数*/
vtxNum = scn.nextInt();
/*图中边数*/
edgeNum = scn.nextInt();
adj = (LinkedList[])new LinkedList[vtxNum];
for(int i = 0; i < vtxNum; i++){
adj[i] = new LinkedList();
}
/*无向图,同一条边,添加两次*/
for(int i = 0; i < edgeNum; i++){
int from = scn.nextInt();
int to = scn.nextInt();
Edge e1 = new Edge(from, to);
Edge e2 = new Edge(to, from);
adj[from].add(e1);
adj[to].add(e2);
}
scn.close();
}
/*图的显示方法*/
@Override
public String toString(){
StringWriter sw = new StringWriter();
PrintWriter pw = new PrintWriter(sw);
for (int i = 0; i < vtxNum; i++) {
pw.printf(" %-3d: ", i);
for (Edge e : adj[i]) {
pw.print(e);
}
pw.println();
}
return sw.getBuffer().toString();
}
/*返回顶点个数*/
public int vtxNum(){
return vtxNum;
}
/*返回边的数量*/
public int edgeNum(){
return edgeNum;
}
}
public CutVerEdge(UndirectedGraph ug){
this.ug = ug;
marked = new boolean[ug.vtxNum()];
low = new int[ug.vtxNum()];
dfn = new int[ug.vtxNum()];
parent = new int[ug.vtxNum()];
isCutVer = new boolean[ug.vtxNum()];
listV = new LinkedList();
listE = new LinkedList();
/*调用深度优先遍历,求解各个顶点的dfn值和low值*/
dfs();
}
private void dfs(){
int childTree = 0;
marked[0] = true;
visitOrder = 1;
parent[0] = -1;
for(Edge e : ug.adj[0]){
int w = e.to();
if(!marked[w]){
marked[w] = true;
parent[w] = 0;
dfs0(w);
/*根顶点相连的边是否是桥*/
if(low[w] > dfn[0]){
listE.add(new int[]{0, w});
}
childTree++;
}
}
/*单独处理根顶点*/
if(childTree >= 2){/*根顶点是割点的条件*/
isCutVer[0] = true;
}
}
/*除了根顶点的其它情况*/
private void dfs0(int v){
dfn[v] = low[v] = ++visitOrder;
for(Edge e : ug.adj[v]){
int w = e.to();
if(!marked[w]){
marked[w] = true;
parent[w] = v;
dfs0(w);
low[v] = Math.min(low[v], low[w]);
/*判断割点*/
if(low[w] >= dfn[v]){
isCutVer[v] = true;
/*判断桥*/
if(low[w] > dfn[v]){
listE.add(new int[]{v, w});
}
}
}else
if(parent[v] != w && dfn[w] < dfn[v]){
low[v] = Math.min(low[v], dfn[w]);
}
}
}
/*返回所有割点*/
public List allCutVer(){
for(int i = 0; i < isCutVer.length; i++){
if(isCutVer[i]){
listV.add(i);
}
}
return listV;
}
/*返回所有割边*/
public List allCutEdge(){
return listE;
}
/*判断顶点v是否是割点*/
public boolean isCutVer(int v){
return isCutVer[v];
}
public static void main(String[] args) throws FileNotFoundException{
File path = new File(System.getProperties()
.getProperty("user.dir"))
.getParentFile();
File f = new File(path, "algs4-data/tinyG2.txt");
FileReader fr = new FileReader(f);
UndirectedGraph ug = new UndirectedGraph(fr);
System.out.println("\n-------图的邻接表示法-------");
System.out.println(ug);
System.out.println("\n-------图中的割点-------");
CutVerEdge cve = new CutVerEdge(ug);
for(int i : cve.allCutVer()){
System.out.println(i);
}
System.out.println("\n-------图中的割边-----");
for(int[] a : cve.allCutEdge()){
System.out.println(a[0]+" "+ a[1]);
}
}
}
运行结果
------图的邻接表示法------- 0 : [0, 5] [0, 1] [0, 2] [0, 6] 1 : [1, 0] 2 : [2, 0] 3 : [3, 4] [3, 5] 4 : [4, 3] [4, 6] [4, 5] 5 : [5, 0] [5, 4] [5, 3] 6 : [6, 4] [6, 7] [6, 9] [6, 0] 7 : [7, 8] [7, 6] 8 : [8, 7] 9 : [9, 12] [9, 10] [9, 11] [9, 6] 10 : [10, 9] 11 : [11, 12] [11, 9] 12 : [12, 9] [12, 11] -------图中的割点------- 0 6 7 9 -------图中的割边----- 7 8 6 7 9 10 6 9 0 1 0 2
6. 参考内容
[1]. http://www.cnblogs.com/en-heng/p/4002658.html
[2]. http://blog.csdn.net/wtyvhreal/article/details/43530613
[3]. http://www.cppblog.com/ZAKIR/archive/2010/08/30/124869.html?opt=admin