《Python数据分析与挖掘实战》第13章—— 财政收入影响因素分析及预测模型(lasso回归+DNN+LinearSVR)
文章目录
- 1.挖掘背景及目标
- 2.数据探索
- 2.1 概括性分析描述性统计
- 2.2 计算各个变量之间的皮尔森系数'pearson'/ 'kendall'/ 'spearman'
- 2.3 查看相似属性
- 2.4 绘制相关性热力图
- 3.数据预处理——数据规约
- 3.1 lasso回归模型
- 3.1 降维,lasso回归模型筛选特征
- 4.模型构建
- 4.1 灰色预测
- 4.2 神经网络
- 4.3 线支持向量机线性回归(LinearSVR)
- 4.4 神经网络,LinearSVR模型拟合效果
本文是基于《Python数据分析与挖掘实战》的实战部分的第13章的数据——《财政收入影响因素分析及预测模型》做的分析。
旨在补充原文中的细节代码,并给出文中涉及到的内容的完整代码。
在作者所给代码的基础上增加的内容包括:
1)探索了灰色预测的原理
2)画出预测结果图,数据特征相关性热力图
3)由于书中使用的是AdaptiveLasso,但是没有找到该函数,所以采用了其他变量选择模型
1.挖掘背景及目标
根据1994-2013年相关财政数据 ,梳理影响地方财政收入的关键特征,对未来几年的财政数据进行预测。
实质:回归
2.数据探索
2.1 概括性分析描述性统计
#-*- coding: utf-8 -*-
import numpy as np
import pandas as pd
inputfile = '../data/data1.csv' #输入的数据文件
data = pd.read_csv(inputfile) #读取数据
r = [data.min(), data.max(), data.mean(), data.std()] #依次计算最小值、最大值、均值、标准差
r = pd.DataFrame(r, index = ['Min', 'Max', 'Mean', 'STD']).T #计算相关系数矩阵
print(np.round(r, 2)) #保留两位小数
Min Max Mean STD
x1 3831732.00 7599295.00 5579519.95 1262194.72
x2 181.54 2110.78 765.04 595.70
x3 448.19 6882.85 2370.83 1919.17
x4 7571.00 42049.14 19644.69 10203.02
x5 6212.70 33156.83 15870.95 8199.77
x6 6370241.00 8323096.00 7350513.60 621341.85
x7 525.71 4454.55 1712.24 1184.71
x8 985.31 15420.14 5705.80 4478.40
x9 60.62 228.46 129.49 50.51
x10 65.66 852.56 340.22 251.58
x11 97.50 120.00 103.31 5.51
x12 1.03 1.91 1.42 0.25
x13 5321.00 41972.00 17273.80 11109.19
y 64.87 2088.14 618.08 609.25
2.2 计算各个变量之间的皮尔森系数’pearson’/ ‘kendall’/ ‘spearman’
#-*- coding: utf-8 -*-
import numpy as np
import pandas as pd
inputfile = '../data/data1.csv' #输入的数据文件
data = pd.read_csv(inputfile) #读取数据
print(np.round(data.corr(method = 'pearson'), 2)) #计算相关系数矩阵,保留两位小数
2.3 查看相似属性
association=data.corr()
delSimCol = []
colNum = association.shape[0]###列
print(association.shape[1])
print(colNum)
names = association.columns
for i in range(colNum):
for j in range(i+1,colNum):
if association.iloc[i,j]>0.9:
delSimCol.append((names[i],names[j]))
print('经过筛选得到的相似的属性为:\n',delSimCol)
delCol = [i[1] for i in delSimCol]
print(delCol)
经过筛选得到的相似的属性为:
[('x1', 'x2'), ('x1', 'x3'), ('x1', 'x4'), ('x1', 'x5'), ('x1', 'x6'), ('x1', 'x7'), ('x1', 'x8'), ('x1', 'x9'), ('x1', 'x10'), ('x1', 'x12'), ('x1', 'x13'), ('x1', 'y'), ('x2', 'x3'), ('x2', 'x4'), ('x2', 'x5'), ('x2', 'x6'), ('x2', 'x7'), ('x2', 'x8'), ('x2', 'x9'), ('x2', 'x10'), ('x2', 'x13'), ('x2', 'y'), ('x3', 'x4'), ('x3', 'x5'), ('x3', 'x6'), ('x3', 'x7'), ('x3', 'x8'), ('x3', 'x9'), ('x3', 'x10'), ('x3', 'x13'), ('x3', 'y'), ('x4', 'x5'), ('x4', 'x6'), ('x4', 'x7'), ('x4', 'x8'), ('x4', 'x9'), ('x4', 'x10'), ('x4', 'x12'), ('x4', 'x13'), ('x4', 'y'), ('x5', 'x6'), ('x5', 'x7'), ('x5', 'x8'), ('x5', 'x9'), ('x5', 'x10'), ('x5', 'x13'), ('x5', 'y'), ('x6', 'x7'), ('x6', 'x8'), ('x6', 'x9'), ('x6', 'x10'), ('x6', 'x12'), ('x6', 'x13'), ('x6', 'y'), ('x7', 'x8'), ('x7', 'x9'), ('x7', 'x10'), ('x7', 'x13'), ('x7', 'y'), ('x8', 'x9'), ('x8', 'x10'), ('x8', 'x13'), ('x8', 'y'), ('x9', 'x10'), ('x9', 'x12'), ('x9', 'x13'), ('x9', 'y'), ('x10', 'x12'), ('x10', 'x13'), ('x10', 'y'), ('x13', 'y')]
['x2', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x9', 'x10', 'x12', 'x13', 'y', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x9', 'x10', 'x13', 'y', 'x4', 'x5', 'x6', 'x7', 'x8', 'x9', 'x10', 'x13', 'y', 'x5', 'x6', 'x7', 'x8', 'x9', 'x10', 'x12', 'x13', 'y', 'x6', 'x7', 'x8', 'x9', 'x10', 'x13', 'y', 'x7', 'x8', 'x9', 'x10', 'x12', 'x13', 'y', 'x8', 'x9', 'x10', 'x13', 'y', 'x9', 'x10', 'x13', 'y', 'x10', 'x12', 'x13', 'y', 'x12', 'x13', 'y', 'y']
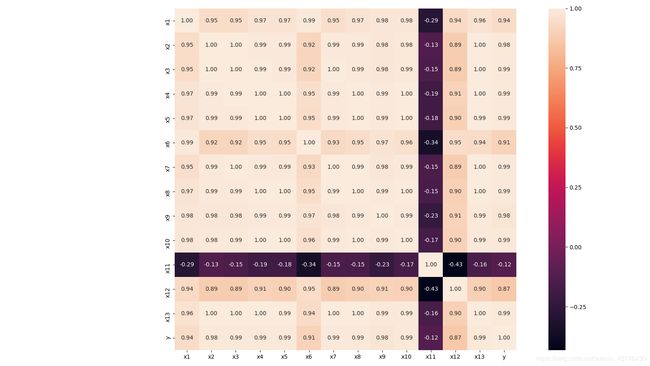
2.4 绘制相关性热力图
- 相关性热力图
#相关性热力图
import matplotlib.pyplot as plt
import seaborn as sns
plt.subplots(figsize=(16,9))
correlation_mat = data.corr()
sns.heatmap(correlation_mat, annot=True, cbar=True, square=True, fmt='.2f', annot_kws={'size': 10})
plt.show()
- 查看影响最终结果的十个变量,并绘制热力图
#查看影响最终价格的十个变量,并绘制热力图
k = 10
plt.figure(figsize=(12,9))
cols = correlation_mat.nlargest(k, 'y')['y']
print(cols)
cols=cols.index
print(cols)
sns.set(font_scale=1.25)
hm = sns.heatmap(data[cols].corr(), cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
- 相关性大于0.5的corr()矩阵
print(correlation_mat[correlation_mat['y']>0.5])
x1 x2 x3 ... x12 x13 y
x1 1.000000 0.946127 0.946105 ... 0.935236 0.961951 0.938657
x2 0.946127 1.000000 0.997153 ... 0.887553 0.997097 0.984676
x3 0.946105 0.997153 1.000000 ... 0.887417 0.997129 0.992741
x4 0.970858 0.992443 0.994579 ... 0.907801 0.996877 0.987478
x5 0.971181 0.989825 0.992625 ... 0.896969 0.994758 0.988964
x6 0.993656 0.919806 0.918570 ... 0.948412 0.938881 0.909062
x7 0.953170 0.990983 0.996440 ... 0.887458 0.995589 0.994115
x8 0.970053 0.993305 0.994398 ... 0.897361 0.998159 0.988947
x9 0.983138 0.979635 0.981389 ... 0.907972 0.988529 0.975441
x10 0.978001 0.983910 0.987977 ... 0.903448 0.992369 0.986830
x12 0.935236 0.887553 0.887417 ... 1.000000 0.897713 0.868982
x13 0.961951 0.997097 0.997129 ... 0.897713 1.000000 0.988245
y 0.938657 0.984676 0.992741 ... 0.868982 0.988245 1.000000
[13 rows x 14 columns]
3.数据预处理——数据规约
3.1 lasso回归模型
-
Lasso回归与岭回归非常相似,因为两种技术都有相同的前提:它们都是在回归优化函数中增加一个偏置项,以减少共线性的影响,从而减少模型方差。然而,不像岭回归那样使用平方偏差,Lasso回归使用绝对值偏差作为正则化项:
岭回归和Lasso回归之间存在一些差异,基本上可以归结为L2和L1正则化的性质差异 -
内置的特征选择(Built-in feature selection):
这是L1范数的一个非常有用的属性,而L2范数不具有这种特性。这实际上因为是L1范数倾向于产生稀疏系数。例如,假设模型有100个系数,但其中只有10个系数是非零系数,这实际上是说“其他90个变量对预测目标值没有用处”。 而L2范数产生非稀疏系数,所以没有这个属性。因此,可以说Lasso回归做了一种“参数选择”形式,未被选中的特征变量对整体的权重为0。 -
稀疏性:
指矩阵(或向量)中只有极少数条目非零。 L1范数具有产生具有零值或具有很少大系数的非常小值的许多系数的属性。 -
计算效率:
L1范数没有解析解,但L2范数有。这使得L2范数的解可以通过计算得到。然而,L1范数的解具有稀疏性,这使得它可以与稀疏算法一起使用,这使得在计算上更有效率。 -
适用场景
当原始特征中存在多重共线性时,Lasso 回归不失为一种很好的处理共线性的方法,它可以有效地对存在多重共线性的特征进行筛选。在机器学习中,面对海量的数据,首先想到的就是降维,争取用尽可能少的数据解决问题,从这层意义上说,用Lasso模型进行特征选择也是种有效的降维方法。从理论上说,Lasso 对数据类型没有太多限制,可以接收任何类型的数据,而且一般不需要对特征进行标准化处理。 -
Lasso回归方法优缺点
Lasso回归方法的优点是可以弥补最小二乘估计法和逐步回归局部最优估计的不足,可以很好地进行特征的选择,有效地解决各特征之间存在多重共线性的问题。缺点是当存在一组高度 相关的特征时, Lasso 回归方法倾向于选择其中的一个特征,而忽视其他所有的特征,这种情况会导致结果的不稳定性。虽然Lasso回归方法存在弊端,但是在合适的场景中还是可以发挥不错的效果的。在财政收人预测中,各原始特征存在着严重的多重共线性,、
3.1 降维,lasso回归模型筛选特征
#-*- coding: utf-8 -*-
import pandas as pd
inputfile = '../data/data1.csv' #输入的数据文件
data = pd.read_csv(inputfile) #读取数据
from sklearn.linear_model import Lasso# AdaptiveLasso找不到
# LASSO回归的特点是在拟合广义线性模型的同时进行变量筛选和复杂度调整。 因此,不论目标因变量是连续的,还是二元或者多元离散的,
#都可以用LASSO回归建模然后预测。 这里的变量筛选是指不把所有的变量都放入模型中进行拟合,而是有选择的把变量放入模型从而得到更好的性能参数。
model = Lasso(alpha = 0.1)
model.fit(data.iloc[:,:13], data['y']) # data.iloc[:, 0:13]
print(model.coef_) # 各个特征权重weight
print(model.intercept_) # 输出偏置bias
[-1.88512448e-04 -2.68436321e-01 4.45960813e-01 -3.24264041e-02
7.25657667e-02 4.52109484e-04 2.28596158e-01 -4.51460904e-02
-3.10503208e+00 6.19423002e-01 4.80398130e+00 -9.79664624e+01
-3.86933684e-02]
-2650.9958943685506
lasso = Lasso(1000) #调用Lasso()函数,设置λ的值为1000
lasso.fit(data.iloc[:,0:13],data['y'])
print('相关系数为:',np.round(lasso.coef_,5)) #输出结果,保留五位小数
## 计算相关系数非零的个数
print('相关系数非零个数为:',np.sum(lasso.coef_ != 0))
print(lasso.coef_.shape)
mask = lasso.coef_ != 0 #返回一个相关系数是否为零的布尔数组
print('相关系数是否为零:',mask)
outputfile = '../tmp/new_reg_data.csv' #输出的数据文件
new_reg_data = data.iloc[:, mask] #返回相关系数非零的数据
new_reg_data.to_csv(outputfile) #存储数据
print('输出数据的维度为:',new_reg_data.shape) #查看输出数据的维度
相关系数为: [-1.8000e-04 -0.0000e+00 1.2414e-01 -1.0310e-02 6.5400e-02 1.2000e-04
3.1741e-01 3.4900e-02 -0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00
-4.0300e-02]
相关系数非零个数为: 8
(13,)
相关系数是否为零: [ True False True True True True True True False False False False True]
输出数据的维度为: (20, 8)
利用Lasso回归方法识别影响财政收人的关键因素是社会从业人数(x1 )、 社会消费品零售总额(x3)、城镇居民人均可支配收人(x4)、 城镇居民人均消费性支出(x5)、年末总人口(x6)全社会固定资产投资额(x7)、地区生产总值(x8)和居民消费水平(x13)。
4.模型构建
由于有多个指标需要预测建模,但是各自又有雷同之处,所以,此处以“某市财政收入预测模型” 为例
4.1 灰色预测
此处利用灰色预测,预测出2014-2015年的各个变量的数据,为接下来建模准备
灰色预测:灰色预测是一种对含有不确定因素的系统进行预测的方法,灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
灰色理论建立的是生成数据模型,不是原始数据模型
数据生成方式:A:累加生成:通过数列间各时刻数据的依个累加得到新的数据与数列。累加前数列为原始数列,累加后为生成数列。B:累减生成 C:其他
- 灰色预测函数
# 灰色预测函数
def GM11(x0): #自定义灰色预测函数 #该函数覆盖了导入的包的同名函数
import numpy as np
x1 = x0.cumsum() #1-AGO序列
z1 = (x1[:len(x1)-1] + x1[1:])/2.0 #紧邻均值(MEAN)生成序列 # 由常微分方程可知,取前后两个时刻的值的平均值代替更为合理
# x0[1] = -1/2.0*(x1[1] + x1[0])
z1 = z1.reshape((len(z1),1))
B = np.append(-z1, np.ones_like(z1), axis = 1) # (***)
Yn = x0[1:].reshape((len(x0)-1, 1))
[[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) #计算参数
# fkplusone = (x1[0]-b/a)*np.exp(-a*k)#时间响应方程 # 由于x0[0] = x1[0]
f = lambda k: (x1[0]-b/a)*np.exp(-a*(k-1))-(x1[0]-b/a)*np.exp(-a*(k-2)) #还原值
delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)])) # 残差
C = delta.std()/x0.std() # 后验比差值
P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
return f, a, b, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率
- 预测2004、2005年的值
#-*- coding: utf-8 -*-
import numpy as np
import pandas as pd
from GM11 import GM11 #引入自己编写的灰色预测函数
inputfile = '../data/data1.csv' #输入的数据文件
outputfile = '../tmp/data1_GM11.xls' #灰色预测后保存的路径
data = pd.read_csv(inputfile) #读取数据
data.index = range(1994, 2014)
data.loc[2014] = None
data.loc[2015] = None
l = ['x1', 'x2', 'x3', 'x4', 'x5', 'x7']
for i in l:
gm = GM11(data[i][:-2].values)
f = gm[0] ##获得灰色预测函数
P = gm[-1] # 获得小残差概率
C = gm[-2] # 获得后验比差值
data[i][2014] = f(len(data)-1) #2014年预测结果
data[i][2015] = f(len(data)) #2015年预测结果
data[i] = data[i].round(2) #保留两位小数
if (C < 0.35 and P > 0.95): # 评测后验差判别
print('对于模型%s,该模型精度为---好' % i)
elif (C < 0.5 and P > 0.8):
print('对于模型%s,该模型精度为---合格' % i)
elif (C < 0.65 and P > 0.7):
print('对于模型%s,该模型精度为---勉强合格' % i)
else:
print('对于模型%s,该模型精度为---不合格' % i)
data[l+['y']].to_excel(outputfile) #结果输出
对于模型x1,该模型精度为---好
对于模型x2,该模型精度为---好
对于模型x3,该模型精度为---好
对于模型x4,该模型精度为---好
对于模型x5,该模型精度为---好
对于模型x7,该模型精度为---好
4.2 神经网络
#-*- coding: utf-8 -*-
import pandas as pd
inputfile = '../tmp/data1_GM11.xls' #灰色预测后保存的路径
outputfile = '../data/revenue.xls' #神经网络预测后保存的结果
modelfile = '../tmp/1-net.model' #模型保存路径
data = pd.read_excel(inputfile) #读取数据
# feature = ['x1', 'x2', 'x3', 'x4', 'x5', 'x7'] #特征所在列
feature = ['x1', 'x3', 'x5'] # 特征所在列
data_train = data.loc[range(1999,2014)].copy() #取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std #数据标准化
x_train = data_train[feature].values #特征数据
y_train = data_train['y'].values #标签数据
from keras.models import Sequential
from keras.layers.core import Dense, Activation
import time
start = time.time()
model = Sequential() #建立模型
model.add(Dense(output_dim =6, input_dim=3))
model.add(Activation('relu')) #用relu函数作为激活函数,能够大幅提供准确度
model.add(Dense(units=1, input_dim=6))
model.compile(loss='mean_squared_error', optimizer='adam') #编译模型
model.fit(x_train, y_train, nb_epoch = 3000, batch_size = 16) #训练模型,学习一万次
model.save_weights(modelfile) #保存模型参数
end = time.time()
usetime = end-start
print('训练该模型耗时'+ str(usetime) +'s!')
#预测,并还原结果。
x = ((data[feature] - data_mean[feature])/data_std[feature]).values
data[u'y_pred'] = model.predict(x) * data_std['y'] + data_mean['y']
data.to_excel(outputfile)
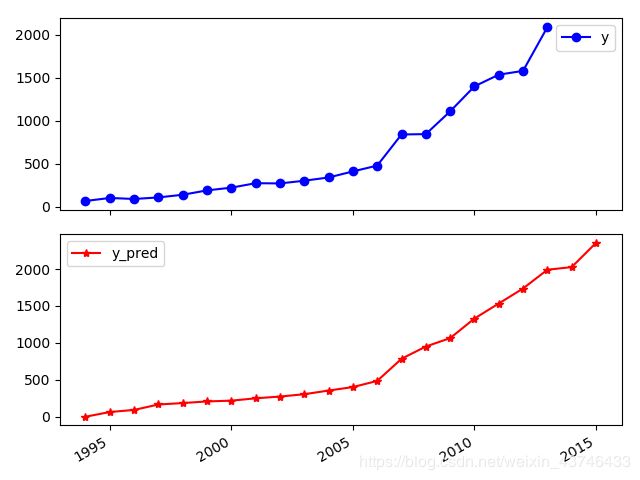
import matplotlib.pyplot as plt #画出预测结果图
p = data[['y','y_pred']].plot(subplots = True, style=['b-o','r-*'])
plt.show()
4.3 线支持向量机线性回归(LinearSVR)
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
data_train = data.loc[range(1994,2014)].copy()#取2014年前的数据建模
print(data_train.shape)
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std #数据标准化
x_train = data_train[feature].values #特征数据
y_train = data_train['y'].values #标签数据
x = ((data[feature] - data_mean[feature]) / data_std[feature]).values #标准差标准化 预测,并还原结果。
linearsvr = LinearSVR().fit(x_train,y_train) #调用LinearSVR()函数
data[u'y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y'] # y
## SVR预测后保存的结果
outputfile = '../tmp/new_reg_data_GM11_revenue.xls'
data.to_excel(outputfile)
print('真实值与预测值分别为:',data[['y','y_pred']])
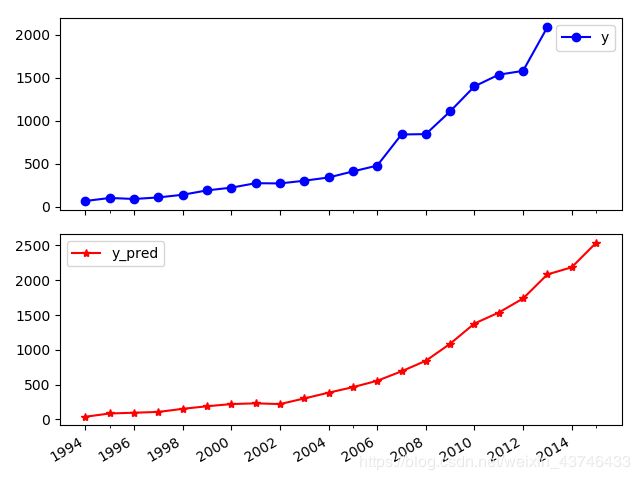
ax1=plt.figure(figsize=(5,5)).add_subplot(2,1,1)
print('预测图为:')
data[['y','y_pred']].plot(subplots = True,style=['b-o','r-*'],xticks=data.index[::2]) ##subplots = True两表分开
plt.show()
真实值与预测值分别为:
y y_pred
1994 64.87 38.430172
1995 99.75 84.892441
1996 88.11 95.687080
1997 106.07 107.330335
1998 137.32 151.754559
1999 188.14 188.707915
2000 219.91 219.947263
2001 271.91 230.712161
2002 269.10 220.141687
2003 300.55 300.823979
2004 338.45 383.574568
2005 408.86 463.169757
2006 476.72 554.688700
2007 838.99 690.833863
2008 843.14 842.275139
2009 1107.67 1086.568108
2010 1399.16 1377.696702
2011 1535.14 1535.140000
2012 1579.68 1737.409000
2013 2088.14 2083.494528
2014 NaN 2185.354793
2015 NaN 2536.021152
4.4 神经网络,LinearSVR模型拟合效果
- dnn
from sklearn.metrics import explained_variance_score,\
mean_absolute_error,mean_squared_error,\
median_absolute_error,r2_score
data=data[:-2]
print('平均绝对误差为:',mean_absolute_error(data['y'].values,data['y_pred'].values))
print('均方误差为:',mean_squared_error(data['y'],data['y_pred']))
print('中值绝对误差为:',median_absolute_error(data['y'],data['y_pred']))
print('可解释方差值为:',explained_variance_score(data['y'],data['y_pred']))
print('R方值为:',r2_score(data['y'],data['y_pred']))
平均绝对误差为: 47.34970288085937
均方误差为: 4967.7319640722835
中值绝对误差为: 17.800775756835947
可解释方差值为: 0.98689966862744
R方值为: 0.9859123984239436
- LinearSVR
平均绝对误差为: 34.27321657516803
均方误差为: 3224.483503621415
中值绝对误差为: 17.69311546022425
可解释方差值为: 0.9908669137713841
R方值为: 0.9908559400514944