复变函数——学习笔记4:复变函数的积分
复变函数的积分
- 复变函数的积分
- 柯西积分定理——积分与路径无关
- 柯西积分定理及其应用
- 柯西积分定理的证明
- 柯西积分定理的变式
- 单连通闭区域情形
- 多连通区域情形
- 柯西积分公式
- 柯西积分公式的证明
- 解析函数的无穷可微性
- 刘维尔定理及代数基本定理
- 莫雷拉定理
复变函数的积分
复变函数积分的定义和数学分析中的曲线积分的定义很类似。
定义4.1 L L L是复平面上的一条可求长曲线,复变函数 w = f ( z ) w=f(z) w=f(z)在 L L L上有定义, L L L的起止点分别为 z 0 , z 0 ′ z_0,z_0^\prime z0,z0′,从 z 0 z_0 z0到 z 0 ′ z_0^\prime z0′依次取分点 z 0 , z 1 , ⋯ , z n = z 0 ′ z_0,z_1,\cdots,z_n=z_0^\prime z0,z1,⋯,zn=z0′,称为 L L L的一个分划,记为 Δ \Delta Δ, z i − 1 z_{i-1} zi−1到 z i z_i zi的曲线段记为 L i ( i = 1 , ⋯ , n ) L_i(i=1,\cdots,n) Li(i=1,⋯,n), λ ( Δ ) = max 1 ≤ i ≤ n ∣ L i ∣ \displaystyle\lambda(\Delta)=\max_{1\le i\le n}|L_i| λ(Δ)=1≤i≤nmax∣Li∣,如果存在复数 I I I,对任意的 ε > 0 \varepsilon>0 ε>0,存在 δ > 0 \delta>0 δ>0,对任意的分划 Δ \Delta Δ,只要 λ ( Δ ) < δ \lambda(\Delta)<\delta λ(Δ)<δ,任取 ξ i ∈ L i ( i = 1 , ⋯ , n ) \xi_i\in L_i(i=1,\cdots,n) ξi∈Li(i=1,⋯,n),都有 ∣ ∑ k = 1 n f ( ξ k ) ( z k − z k − 1 ) − I ∣ < ε \left|\sum_{k=1}^nf(\xi_k)(z_k-z_{k-1})-I\right|<\varepsilon ∣∣∣∣∣k=1∑nf(ξk)(zk−zk−1)−I∣∣∣∣∣<ε则称 w = f ( z ) w=f(z) w=f(z)在 L L L上可积, I I I为 w = f ( z ) w=f(z) w=f(z)沿着 L L L从 z 0 z_0 z0到 z 0 ′ z_0^\prime z0′的积分,记为 ∫ L f ( z ) d z \displaystyle \int_Lf(z)dz ∫Lf(z)dz
现在我们来考察一下以上定义中的和式 ∑ k = 1 n f ( ξ k ) Δ z k \sum_{k=1}^nf(\xi_k)\Delta z_k k=1∑nf(ξk)Δzk设 f = u + v i f=u+vi f=u+vi, Δ z k = Δ x k + i Δ y k \Delta z_k=\Delta x_k+i\Delta y_k Δzk=Δxk+iΔyk,则 ∑ k = 1 n f ( ξ k ) Δ z k = ∑ k = 1 n [ u ( ξ k ) + v ( ξ k ) i ] [ Δ x k + i Δ y k ] = ∑ k = 1 n [ ( u ( ξ k ) Δ x k − v ( ξ k ) Δ y k ) + i ( u ( ξ k ) Δ y k + v ( ξ k ) Δ x k ) ] \begin{aligned} &\sum_{k=1}^nf(\xi_k)\Delta z_k=\sum_{k=1}^n[u(\xi_k)+v(\xi_k)i][\Delta x_k+i\Delta y_k]\\ =&\sum_{k=1}^n[(u(\xi_k)\Delta x_k-v(\xi_k)\Delta y_k)+i(u(\xi_k)\Delta y_k+v(\xi_k)\Delta x_k)] \end{aligned} =k=1∑nf(ξk)Δzk=k=1∑n[u(ξk)+v(ξk)i][Δxk+iΔyk]k=1∑n[(u(ξk)Δxk−v(ξk)Δyk)+i(u(ξk)Δyk+v(ξk)Δxk)]取极限即可得到 ∫ L f ( z ) d z = ∫ L u d x − v d y + i ∫ L u d y + v d x \int_Lf(z)dz=\int_Ludx-vdy+i\int_Ludy+vdx ∫Lf(z)dz=∫Ludx−vdy+i∫Ludy+vdx我们就得到了复积分和曲线积分之间的联系,我们再改写一下以上的等式,为 ∫ L f ( z ) d z = ∫ L ( u + i v ) ( d x + i d y ) \int_Lf(z)dz=\int_L(u+iv)(dx+idy) ∫Lf(z)dz=∫L(u+iv)(dx+idy)容易验证形式上 ∫ L ( u + i v ) ( d x + i d y ) = ∫ L u d x − v d y + i ∫ L u d y + v d x \int_L(u+iv)(dx+idy)=\int_Ludx-vdy+i\int_Ludy+vdx ∫L(u+iv)(dx+idy)=∫Ludx−vdy+i∫Ludy+vdx写成左边的形式就很方便对积分计算公式进行记忆。如果 L L L是光滑曲线 x = z ( t ) = x ( t ) + y ( t ) i , a ≤ t ≤ b x=z(t)=x(t)+y(t)i,a\le t\le b x=z(t)=x(t)+y(t)i,a≤t≤b,由数学分析中曲线积分的计算公式,我们还可以得到 ∫ L f ( z ) d z = ∫ a b f ( z ( t ) ) z ′ ( t ) d t \int_Lf(z)dz=\int_a^bf(z(t))z^\prime(t)dt ∫Lf(z)dz=∫abf(z(t))z′(t)dt其中 z ′ ( t ) = x ′ ( t ) + i y ′ ( t ) z^\prime(t)=x^\prime(t)+iy^\prime(t) z′(t)=x′(t)+iy′(t),这就为我们提供了复积分的参数方程计算方法。下面我们列举复积分的若干性质:
(1) f ( z ) , g ( z ) f(z),g(z) f(z),g(z)在曲线 L L L上可积,则对任意的复数 α , β \alpha,\beta α,β, α f ( z ) + β g ( z ) \alpha f(z)+\beta g(z) αf(z)+βg(z)在 L L L上可积,并且 ∫ L [ α f ( z ) + β g ( z ) ] d z = α ∫ L f ( z ) d z + β ∫ L g ( z ) d z \int_L[\alpha f(z)+\beta g(z)]dz=\alpha\int_Lf(z)dz+\beta\int_Lg(z)dz ∫L[αf(z)+βg(z)]dz=α∫Lf(z)dz+β∫Lg(z)dz(2) L L L由 L 1 , L 2 L_1,L_2 L1,L2衔接得到, f f f在 L L L上可积的充要条件是 f f f在 L 1 , L 2 L_1,L_2 L1,L2上可积,并且 ∫ L f ( z ) d z = ∫ L 1 f ( z ) d z + ∫ L 2 f ( z ) d z \int_Lf(z)dz=\int_{L_1}f(z)dz+\int_{L_2}f(z)dz ∫Lf(z)dz=∫L1f(z)dz+∫L2f(z)dz(3) L L L的起止点为 z 0 , z 0 ′ z_0,z_0^\prime z0,z0′,记 z 0 ′ z_0^\prime z0′到 z 0 z_0 z0沿着 L L L的曲线为 L − L^- L−, f ( z ) f(z) f(z)在 L L L上可积,则 f ( z ) f(z) f(z)在 L − L^{-} L−上可积,并且 ∫ L f ( z ) d z = − ∫ L − f ( z ) d z \int_Lf(z)dz=-\int_{L^-}f(z)dz ∫Lf(z)dz=−∫L−f(z)dz(4) f ( z ) f(z) f(z)在 L L L可积,则 ∣ ∫ L f ( z ) d z ∣ ≤ ∫ L ∣ f ( z ) ∣ d s \left|\int_Lf(z)dz\right|\le\int_L|f(z)|ds ∣∣∣∣∫Lf(z)dz∣∣∣∣≤∫L∣f(z)∣ds其中右边是第一型曲线积分
(5)(积分估值)若沿着曲线 L L L,函数 f ( z ) f(z) f(z)连续,且有正数 M M M使 ∣ f ( z ) ∣ ≤ M ( ∀ z ∈ L ) |f(z)|\le M(\forall z\in L) ∣f(z)∣≤M(∀z∈L),设 L L L其长度为 ∣ L ∣ |L| ∣L∣,则 ∣ ∫ L f ( z ) d z ∣ ≤ M ∣ L ∣ \left|\int_Lf(z)dz\right|\le M|L| ∣∣∣∣∫Lf(z)dz∣∣∣∣≤M∣L∣
下面给出一个重要的积分
例5.1 计算 ∫ C d z z − z 0 \displaystyle\int_C\frac{dz}{z-z_0} ∫Cz−z0dz,其中 C C C为以 ∣ z − z 0 ∣ = r |z-z_0|=r ∣z−z0∣=r,方向取正向
解:
取参数方程 z = z 0 + r e θ i z=z_0+re^{\theta i} z=z0+reθi,则 d z d θ = i r e θ i \frac{dz}{d\theta}=ire^{\theta i} dθdz=ireθi,因此 ∫ C d z z − z 0 = ∫ 0 2 π i r e θ i r e θ i d θ = 2 π i \int_C\frac{dz}{z-z_0}=\int_0^{2\pi}\frac{ire^{\theta i}}{re^{\theta i}}d\theta=2\pi i ∫Cz−z0dz=∫02πreθiireθidθ=2πi
柯西积分定理——积分与路径无关
柯西积分定理及其应用
柯西积分定理和柯西积分公式是本章的核心定理,柯西积分定理是有关复积分与路径无关的定理,考察例5.1就知道复积分并不总是与路径无关,柯西积分定理如下:
定理5.1(柯西积分定理) f ( z ) f(z) f(z)在单连通区域 G G G上解析,则对 G G G内任何逐段光滑的闭曲线 C C C,都有 ∫ C f ( z ) d z = 0 \int_Cf(z)dz=0 ∫Cf(z)dz=0
我们后面再给出柯西积分定理的证明,在给出证明之前,我们先给出柯西积分定理的应用,有了柯西积分定理,我们就可以得出结论,如果 f ( z ) f(z) f(z)在单连通区域 G G G上解析,则积分 ∫ L f ( z ) d z \displaystyle\int_Lf(z)dz ∫Lf(z)dz只与起止点有关,而与积分路径无关,则积分就可以写成 ∫ z 0 z f ( ξ ) d ξ \int_{z_0}^{z}f(\xi)d\xi ∫z0zf(ξ)dξ其中 z 0 z_0 z0为 L L L的起点, z z z为 L L L的终点。任取 z 0 ∈ G z_0\in G z0∈G,我们在 G G G内定义函数 G ( z ) = ∫ z 0 z f ( ξ ) d ξ G(z)=\int_{z_0}^zf(\xi)d\xi G(z)=∫z0zf(ξ)dξ下面我们将证明 G ( z ) G(z) G(z)是解析的,对于 z ∈ G z\in G z∈G,存在 δ > 0 \delta>0 δ>0,使得 z z z以 δ \delta δ为半径的邻域 B ( z , δ ) B(z,\delta) B(z,δ)都在 G G G内,那么对 z ′ ∈ B ( z , δ ) z^\prime\in B(z,\delta) z′∈B(z,δ), z z z和 z ′ z^\prime z′间的直线段 L L L都在 G G G内 G ( z ′ ) − G ( z ) = ∫ L f ( ξ ) d ξ G(z^\prime)-G(z)=\int_Lf(\xi)d\xi G(z′)−G(z)=∫Lf(ξ)dξ取 L L L的参数方程为 z = z ( t ) = ( 1 − t ) z + t z ′ , 0 ≤ t ≤ 1 z=z(t)=(1-t)z+tz^\prime,0\le t\le 1 z=z(t)=(1−t)z+tz′,0≤t≤1,则 G ( z ′ ) − G ( z ) = Δ z ∫ 0 1 f ( z ( t ) ) d t G(z^\prime)-G(z)=\Delta z\int_0^1f(z(t))dt G(z′)−G(z)=Δz∫01f(z(t))dt设 f = u + v i f=u+vi f=u+vi,由定积分的积分中值定理,存在 ξ , ζ ∈ ( 0 , 1 ) \xi,\zeta\in(0,1) ξ,ζ∈(0,1)使得 ∫ 0 1 u ( z ( t ) ) d t = u ( z ( ξ ) ) ∫ 0 1 v ( z ( t ) ) d t = v ( z ( ζ ) ) \int_0^1u(z(t))dt=u(z(\xi))\\ \int_0^1v(z(t))dt=v(z(\zeta)) ∫01u(z(t))dt=u(z(ξ))∫01v(z(t))dt=v(z(ζ))于是 G ( z ′ ) − G ( z ) = Δ z [ u ( z ( ξ ) ) + i v ( z ( ζ ) ) ] G(z^\prime)-G(z)=\Delta z[u(z(\xi))+iv(z(\zeta))] G(z′)−G(z)=Δz[u(z(ξ))+iv(z(ζ))]即 lim Δ z → 0 G ( z ′ ) − G ( z ) Δ z = u ( z ) + i v ( z ) = f ( z ) \lim_{\Delta z\to 0}\frac{G(z^\prime)-G(z)}{\Delta z}=u(z)+iv(z)=f(z) Δz→0limΔzG(z′)−G(z)=u(z)+iv(z)=f(z)这就说明了 G ( z ) G(z) G(z)解析,并且 G ′ ( z ) = f ( z ) G^\prime(z)=f(z) G′(z)=f(z),以上过程如果假设放松为 f ( z ) f(z) f(z)连续,并且 f ( z ) f(z) f(z)在 G G G内的积分与路径无关,也是成立的。如果在 G G G上的解析函数 g ( z ) g(z) g(z)满足 g ′ ( z ) = 0 , ∀ z ∈ G g^\prime(z)=0,\forall z\in G g′(z)=0,∀z∈G,那么, G ( z ) G(z) G(z)为常数(容易证明,这里省略)。那么如果 f ( z ) f(z) f(z)在单连通区域 G G G上解析,那么 f ( z ) f(z) f(z)上 G G G上任意原函数只相差一个常复数,如果我们找到 f ( z ) f(z) f(z)的一个原函数 F ( z ) F(z) F(z),则 F ( z ) = G ( z ) + C F(z)=G(z)+C F(z)=G(z)+C,那么对 z 1 , z 2 ∈ G z_1,z_2\in G z1,z2∈G,就有 ∫ z 1 z 2 f ( z ) d z = G ( z 2 ) − G ( z 1 ) = F ( z 2 ) − F ( z 1 ) \int_{z_1}^{z_2}f(z)dz=G(z_2)-G(z_1)=F(z_2)-F(z_1) ∫z1z2f(z)dz=G(z2)−G(z1)=F(z2)−F(z1)这就是复数域上的微积分基本定理
例5.2 在单连通区域 D : − π < a r g z < π D:-\pi
例5.3 计算复积分 ∫ 0 π + 2 i cos z 2 d z \displaystyle \int_0^{\pi+2i}\cos\frac{z}{2}dz ∫0π+2icos2zdz
解:
w = cos z 2 w=\cos\frac{z}{2} w=cos2z在全平面上解析,其原函数为 2 sin z 2 2\sin\frac{z}{2} 2sin2z,则 ∫ 0 π + 2 i cos z 2 d z = 2 [ sin z 2 ] 0 π + 2 i = 2 sin ( π 2 + i ) = e + 1 e \int_0^{\pi+2i}\cos\frac{z}{2}dz=2[\sin\frac{z}{2}]_0^{\pi+2i}=2\sin{(\frac{\pi}{2}+i)}=e+\frac{1}{e} ∫0π+2icos2zdz=2[sin2z]0π+2i=2sin(2π+i)=e+e1
柯西积分定理的证明
下面我们来证明柯西积分定理:观察 C . − R . C.-R. C.−R.方程:
u x ′ = v y ′ u y ′ = − v x ′ u_x^\prime=v_y^\prime\\ u_y^\prime=-v_x^\prime ux′=vy′uy′=−vx′假设 f ′ ( z ) f^\prime(z) f′(z)是连续的,并且设 f = u + v i f=u+vi f=u+vi,如果 C C C是逐段光滑的简单闭曲线,我们前面推导过 ∫ C f ( z ) d z = ∫ C u d x − v d y + i ∫ C v d x + u d y \int_Cf(z)dz=\int_Cudx-vdy+i\int_Cvdx+udy ∫Cf(z)dz=∫Cudx−vdy+i∫Cvdx+udy我们对两个线积分分别采用格林公式 ∫ C u d x − v d y = ∫ D − v x ′ − u y ′ d x d y = 0 ∫ C v d x + u d y = ∫ D u x ′ − v y ′ d x d y = 0 \int_Cudx-vdy=\int_D -v_x^\prime-u_y^\prime dxdy=0\\ \int_Cvdx+udy=\int_Du_x^\prime-v_y^\prime dxdy=0 ∫Cudx−vdy=∫D−vx′−uy′dxdy=0∫Cvdx+udy=∫Dux′−vy′dxdy=0有 ∫ C f ( z ) d z = 0 \int_Cf(z)dz=0 ∫Cf(z)dz=0这可能是柯西积分定理的灵感来源,但是证明柯西积分定理不能采用格林公式,因为 f ′ ( z ) f^\prime(z) f′(z)不一定是连续的(当然,我们后面会证明解析函数是无穷次可微的, f ′ ( z ) f^\prime(z) f′(z)是连续的,但是这需要用到柯西积分定理证明的柯西积分公式,如果采用这个结果,就会循环论证)。古尔萨给出了一个不需要用到格林公式的证明,我们先大致阐述一下这个证明的思路:
(1)第一步,证明如果闭曲线 C C C是一个包含在 G G G内的三角形区域的边界,柯西积分定理成立
(2)第二步,对于任何包含在 G G G内的多边形,我们将多边形分解成若干三角形之并,添加的连线在不同的三角形边界线积分计算中,方向相反,因而正负相消,最后只剩下多边形的边界,从而证明多边形也满足柯西积分定理(见下图:将多边形分解为三角形之并)
(3)对任意的闭曲线,用一个闭折线逼近这个积分,由于任意的闭折线的积分都为0,而沿着这条闭曲线的积分可以任意接近0,就证得了闭曲线的积分为0
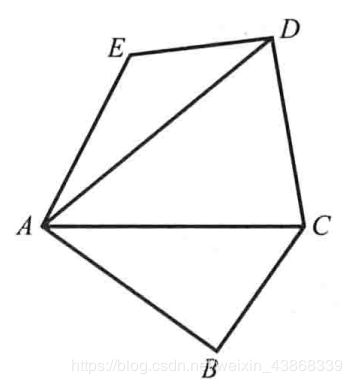
我们先来完成第一步:如果三角形闭区域 Δ \Delta Δ包含在 G G G内,我们取三条边的中点,连接三个中点,得到四个全等的三角形 Δ 1 , Δ 2 , Δ 3 , Δ 4 \Delta_1,\Delta_2,\Delta_3,\Delta_4 Δ1,Δ2,Δ3,Δ4,这里的 Δ \Delta Δ表示三角形区域的圆周, Δ , Δ 1 , Δ 2 , Δ 3 , Δ 4 \Delta,\Delta_1,\Delta_2,\Delta_3,\Delta_4 Δ,Δ1,Δ2,Δ3,Δ4均取正向。
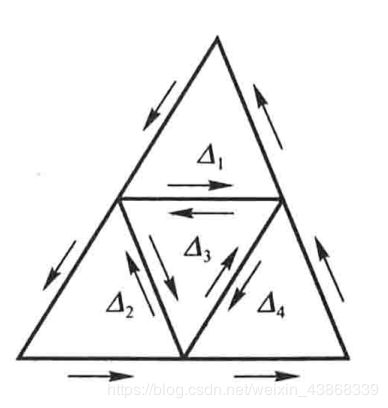
可以看到添加的连线积分方向恰好相反,正负相消,就得到 ∫ Δ f ( z ) d z = ∫ Δ 1 f ( z ) d z + ∫ Δ 2 f ( z ) d z + ∫ Δ 3 f ( z ) d z + ∫ Δ 4 f ( z ) d z \int_\Delta f(z)dz=\int_{\Delta_1}f(z)dz+\int_{\Delta_2}f(z)dz+\int_{\Delta_3}f(z)dz+\int_{\Delta_4}f(z)dz ∫Δf(z)dz=∫Δ1f(z)dz+∫Δ2f(z)dz+∫Δ3f(z)dz+∫Δ4f(z)dz设 ∣ ∫ Δ f ( z ) d z ∣ = M \left|\int_\Delta f(z)dz\right|=M ∣∣∣∣∫Δf(z)dz∣∣∣∣=M我们来证明 M = 0 M=0 M=0,那么必定存在 i 1 = 1 , 2 , 3 或 4 i_1=1,2,3或4 i1=1,2,3或4,满足 ∣ ∫ Δ i 1 f ( z ) d z ∣ ≥ M 4 \left|\int_{\Delta_{i_1}}f(z)dz\right|\ge\frac{M}{4} ∣∣∣∣∣∫Δi1f(z)dz∣∣∣∣∣≥4M我们记这个三角形为 D i 1 1 D^1_{i_1} Di11,对于 D i 1 1 D^1_{i_1} Di11我们也用同样的办法,连接三边中点将其分为四个全等三角形 Δ 2 1 , Δ 2 2 , Δ 3 2 , Δ 4 2 \Delta^1_2,\Delta_2^2,\Delta_3^2,\Delta_4^2 Δ21,Δ22,Δ32,Δ42,则存在 i 2 = 1 , 2 , 3 或 4 i_2=1,2,3或4 i2=1,2,3或4,有 ∣ ∫ Δ i 2 2 f ( z ) d z ∣ ≥ M 16 \left|\int_{\Delta_{i_2}^2}f(z)dz\right|\ge\frac{M}{16} ∣∣∣∣∣∫Δi22f(z)dz∣∣∣∣∣≥16M Δ i 2 2 \Delta_{i_2}^2 Δi22与 Δ i 1 1 \Delta_{i_1}^1 Δi11相似,周长为其 1 2 \frac{1}{2} 21且包含在其内,对 Δ i 2 2 \Delta_{i_2}^2 Δi22也作同样的操作,得到一个完全包含在 Δ i 2 2 \Delta_{i_2}^2 Δi22内相似与 Δ i 2 2 \Delta_{i_2}^2 Δi22的三角形 Δ i 3 3 \Delta_{i_3}^3 Δi33,满足 ∣ ∫ Δ i 3 3 f ( z ) d z ∣ ≥ M 64 \left|\int_{\Delta_{i_3}^3}f(z)dz\right|\ge\frac{M}{64} ∣∣∣∣∣∫Δi33f(z)dz∣∣∣∣∣≥64M其周长为 Δ i 2 2 \Delta_{i_2}^2 Δi22的 1 2 \frac{1}{2} 21,以此类推。得到一个三角形序列 { Δ i n n } \{\Delta_{i_n}^n\} {Δinn},作为区域时 Δ i n n ⊂ Δ i n − 1 n − 1 \Delta_{i_n}^n\subset \Delta_{i_{n-1}}^{n-1} Δinn⊂Δin−1n−1,周长为 Δ i n − 1 n − 1 \Delta_{i_{n-1}}^{n-1} Δin−1n−1的 1 2 \frac{1}{2} 21,因此其周长为 L 2 n \frac{L}{2^n} 2nL,其中 L L L为 Δ \Delta Δ的周长,并且 ∣ ∫ Δ i n n f ( z ) d z ∣ ≥ M 4 n \left|\int_{\Delta_{i_n}^n}f(z)dz\right|\ge \frac{M}{4^n} ∣∣∣∣∣∫Δinnf(z)dz∣∣∣∣∣≥4nM记 Δ i n n = Δ n \Delta_{i_n}^{n}=\Delta_n Δinn=Δn,有 ∫ Δ n d z = 0 \int_{\Delta_n}dz=0 ∫Δndz=0这是因为 Δ n \Delta_n Δn是闭曲线,由复积分的定义就可以直接验证,其次 ∫ Δ n z d z = ∫ Δ n x d x − y d y + i ∫ Δ n x d y + y d x \int_{\Delta_n}zdz=\int_{\Delta_n}xdx-ydy+i\int_{\Delta_n}xdy+ydx ∫Δnzdz=∫Δnxdx−ydy+i∫Δnxdy+ydx用格林公式即可验证 ∫ Δ n z d z = 0 \displaystyle\int_{\Delta_n}zdz=0 ∫Δnzdz=0,实际上, { Δ n } \{\Delta_n\} {Δn}构成一个闭区间套,存在一点 z 0 z_0 z0,属于所有 Δ n \Delta_n Δn(此时作为区域而不是周线),由于 f ( z ) f(z) f(z)在 z 0 z_0 z0处可微,对任意的 ε > 0 \varepsilon>0 ε>0,存在 δ > 0 \delta>0 δ>0,当 ∣ z − z 0 ∣ < δ |z-z_0|<\delta ∣z−z0∣<δ时 ∣ f ( z ) − f ( z 0 ) z − z 0 − f ′ ( z 0 ) ∣ < ε \left|\frac{f(z)-f(z_0)}{z-z_0}-f^\prime(z_0)\right|<\varepsilon ∣∣∣∣z−z0f(z)−f(z0)−f′(z0)∣∣∣∣<ε即 ∣ f ( z ) − f ( z 0 ) − f ′ ( z 0 ) ( z − z 0 ) ∣ < ε ∣ z − z 0 ∣ |f(z)-f(z_0)-f^\prime(z_0)(z-z_0)|<\varepsilon|z-z_0| ∣f(z)−f(z0)−f′(z0)(z−z0)∣<ε∣z−z0∣存在 n 0 n_0 n0, n ≥ n 0 n\ge n_0 n≥n0时,三角形 Δ n \Delta_n Δn,完全包含在 z 0 z_0 z0的邻域内,有 ∫ Δ n f ( z ) d z = ∫ Δ n [ f ( z ) − f ( z 0 ) − f ( z 0 ) ( z − z 0 ) ] d z \int_{\Delta_{n}}f(z)dz=\int_{\Delta_{n}}[f(z)-f(z_0)-f^(z_0)(z-z_0)]dz ∫Δnf(z)dz=∫Δn[f(z)−f(z0)−f(z0)(z−z0)]dz此时1 ∣ ∫ Δ n f ( z ) d z ∣ ≤ ε L 2 4 n \left|\int_{\Delta_{n}}f(z)dz\right|\le \frac{\varepsilon L^2}{4^n} ∣∣∣∣∫Δnf(z)dz∣∣∣∣≤4nεL2故 M < ε L 2 M<\varepsilon L^2 M<εL2由 ε \varepsilon ε的任意性, M = 0 M=0 M=0
于是容易证明:任意包含在 G G G内的闭折线 C C C,都有 ∫ C f ( z ) d z \int_Cf(z)dz ∫Cf(z)dz因此,我们对于一般的曲线,我们只要用一条闭折线取代之即可。那么如何取代呢?取代的合理性又在哪?我们可以仿照数学分析中证明积分与路径无关的条件时采取的手段,引入星形区域:如果区域 G G G内存在一点 z 0 z_0 z0, ∀ z ∈ G \forall z\in G ∀z∈G,直线段 z 0 z z_0z z0z整个包含在 G G G内,如果 f ( z ) f(z) f(z)在 G G G内解析,引入函数 F ( z ) = ∫ z 0 z f ( ξ ) d ξ F(z)=\int_{z_0z}f(\xi)d\xi F(z)=∫z0zf(ξ)dξ其中积分路径是 z 0 z_0 z0到 z z z的直线段,存在 δ > 0 \delta>0 δ>0,当 Δ z < δ \Delta z<\delta Δz<δ时, z z z到 z + Δ z z+\Delta z z+Δz的直线段包含在 G G G内,则以 z 0 , z , z + Δ z z_0,z,z+\Delta z z0,z,z+Δz为三条边的三角形包含在 G G G内 F ( z + Δ z ) − F ( z ) = ∫ z z + Δ z f ( ξ ) d ξ F(z+\Delta z)-F(z)=\int_{z}^{z+\Delta z}f(\xi)d\xi F(z+Δz)−F(z)=∫zz+Δzf(ξ)dξ类似于前面的证明方法,我们可以知道 F ( z ) F(z) F(z)是 f ( z ) f(z) f(z)在 G G G内的原函数。在数学分析中,我们知道原函数存在是线积分与路径无关的充要条件,在复变函数中也是如此。其证法和数学分析也是类似的。即假设 L : z = z ( t ) L:z=z(t) L:z=z(t)是光滑的,我们可以起止点为 z 1 , z 2 z_1,z_2 z1,z2,那么就有 ∫ L f ( z ) d z = F ( z 2 ) − F ( z 1 ) \int_{L}f(z)dz=F(z_2)-F(z_1) ∫Lf(z)dz=F(z2)−F(z1)对逐段光滑曲线分段讨论即可,于是,只要 L L L是逐段光滑的,起止点为 z 1 , z 2 z_1,z_2 z1,z2,就有微积分基本定理成立 ∫ L f ( z ) d z = F ( z 2 ) − F ( z 1 ) \int_{L}f(z)dz=F(z_2)-F(z_1) ∫Lf(z)dz=F(z2)−F(z1)因此在星形区域内积分与路径无关,开邻域一定是星形区域。对于任意的闭曲线 C C C, C C C的起止点都为为 a a a, C C C与 D c D^c Dc有一段正距离 δ > 0 \delta>0 δ>0,对 C C C作划分 Δ : a = z 0 < z 1 < ⋯ < z n = b \Delta:a=z_0
柯西积分定理的变式
单连通闭区域情形
定理5.2 G G G为复平面上的单连通区域,如果 f ( z ) f(z) f(z)在 G ‾ \overline{G} G上解析,则对于任意包含在 G ‾ \overline{G} G中的逐段光滑的闭曲线 C C C,都有 ∫ C f ( z ) d z = 0 \int_Cf(z)dz=0 ∫Cf(z)dz=0
这一定理的证明相当简单,只要找一个包含 G ‾ \overline{G} G的区域 G ′ G^\prime G′, f ( z ) f(z) f(z)在 G ′ G^\prime G′即可,我们自然就想到有限覆盖定理,对于任意的 z ∈ G ‾ z\in \overline{G} z∈G,都存在邻域 B ( z , δ z ) B(z,\delta_z) B(z,δz), f ( z ) f(z) f(z)在其上解析, G ′ = ⋃ z ∈ G ‾ B ( z , δ z ) \displaystyle G^\prime=\bigcup_{z\in \overline{G}}B(z,\delta_z) G′=z∈G⋃B(z,δz)是开集,并且 G ‾ ⊆ G ′ \overline{G}\subseteq G^\prime G⊆G′, f ( z ) f(z) f(z)在 G ′ G^\prime G′上解析,再应用柯西积分定理即可证得结论。
定理5.3 G G G为复平面上的单连通区域,如果 f ( z ) f(z) f(z)在 G G G中解析,在 G ‾ \overline{G} G上连续,则对于任意包含在 G ‾ \overline{G} G中的逐段光滑的闭曲线 C C C,都有 ∫ C f ( z ) d z = 0 \int_Cf(z)dz=0 ∫Cf(z)dz=0
定理5.3的证明相当复杂,一个初等的证明可见杜长国《推广的Cauchy定理的初等证明》一文,这里不证。
多连通区域情形
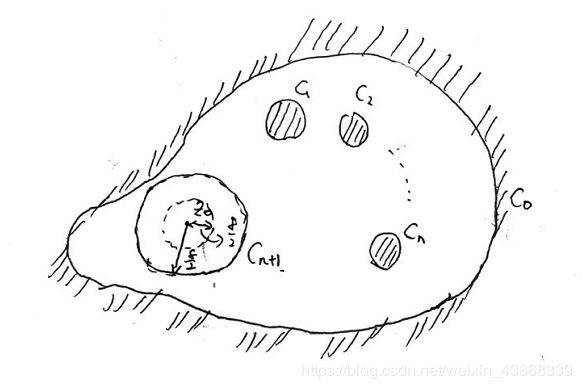
定理5.4 C 0 , C 1 , ⋯ , C n C_0,C_1,\cdots,C_n C0,C1,⋯,Cn是 n + 1 n+1 n+1条逐段光滑的两两不交的简单闭曲线,其中 C 1 , ⋯ , C n C_1,\cdots,C_n C1,⋯,Cn中每一条都在其余各条的外区域内, C 1 , ⋯ , C n C_1,\cdots,C_n C1,⋯,Cn在 C 0 C_0 C0的内区域中,则 C 0 , C 1 , ⋯ , C n C_0,C_1,\cdots,C_n C0,C1,⋯,Cn共同围成一个 n + 1 n+1 n+1连通区域 D D D,如果我们记 C 0 C_0 C0取正向, C 1 , ⋯ , C n C_1,\cdots,C_n C1,⋯,Cn取负向的曲线为 C C C,如果 f ( z ) f(z) f(z)在 D D D中解析,在 D ‾ \overline{D} D上连续,则 ∫ C f ( z ) d z = ∫ C 0 f ( z ) d z − ∑ k = 1 n ∫ C k f ( z ) d z = 0 \int_C f(z)dz=\int_{C_0}f(z)dz-\sum_{k=1}^n\int_{C_k}f(z)dz=0 ∫Cf(z)dz=∫C0f(z)dz−k=1∑n∫Ckf(z)dz=0
以上的 C C C我们又称为复周线,一条逐段可微闭曲线我们称为单周线,单周线和复周线统称为周线,类似于格林公式的证明,我们只要加若干条可微曲线,就可以把 D D D划分为若干个单连通区域或把 D D D切割成单连通区域,所加的曲线积分为0,就可以证得上面的定理。如下图:

柯西积分公式
柯西积分公式的证明
有了柯西积分定理,就可以证明柯西积分公式。
定理5.5(柯西积分公式) f ( z ) f(z) f(z)在周线 C C C(单周线或复周线)围成的区域 D D D上解析, D ‾ \overline{D} D上连续,对任取的 z 0 ∈ D z_0\in D z0∈D,都有 2 π i f ( z 0 ) = ∫ C f ( z ) z − z 0 d z 2\pi if(z_0)=\int_C\frac{f(z)}{z-z_0}dz 2πif(z0)=∫Cz−z0f(z)dz
证:
对于 z 0 z_0 z0,存在 ρ > 0 \rho>0 ρ>0,使得闭邻域 B ‾ ( z 0 , ρ ) ⊆ D \overline{B}(z_0,\rho)\subseteq D B(z0,ρ)⊆D,对 r ≤ ρ r\le \rho r≤ρ,记 D r = D − B ‾ ( z 0 , r ) D_r=D-\overline{B}(z_0,r) Dr=D−B(z0,r), f ( z ) z − z 0 \frac{f(z)}{z-z_0} z−z0f(z)在 D r ‾ \overline{D_r} Dr上解析,在其闭包连续,由定理5.4,有 ∫ ∣ z − z 0 ∣ = r f ( z ) z − z 0 d z = ∫ C f ( z ) z − z 0 d z \int_{|z-z_0|=r}\frac{f(z)}{z-z_0}dz=\int_C\frac{f(z)}{z-z_0}dz ∫∣z−z0∣=rz−z0f(z)dz=∫Cz−z0f(z)dz由于 f ( z ) f(z) f(z)在 z 0 z_0 z0处可微,则对任意的 ε > 0 \varepsilon>0 ε>0,存在 δ > 0 \delta>0 δ>0,当 ∣ z − z 0 ∣ < δ |z-z_0|<\delta ∣z−z0∣<δ时,有 ∣ f ( z 0 ) − f ( z ) ∣ < ε |f(z_0)-f(z)|<\varepsilon ∣f(z0)−f(z)∣<ε令 r < δ r<\delta r<δ,就有 ∣ ∫ ∣ z − z 0 ∣ = r f ( z ) z − z 0 d z − ∫ ∣ z − z 0 ∣ = r f ( z 0 ) z − z 0 d z ∣ ≤ ∫ ∣ z − z 0 ∣ = r ∣ f ( z ) − f ( z 0 ) ∣ ∣ z − z 0 ∣ d s = 1 r ∫ ∣ z − z 0 ∣ = r ∣ f ( z ) − f ( z 0 ) ∣ d z ≤ 2 ε π \begin{aligned} &\left|\int_{|z-z_0|=r}\frac{f(z)}{z-z_0}dz-\int_{|z-z_0|=r}\frac{f(z_0)}{z-z_0}dz\right|\\ \le&\int_{|z-z_0|=r}\frac{|f(z)-f(z_0)|}{|z-z_0|}ds\\ =&\frac{1}{r}\int_{|z-z_0|=r}|f(z)-f(z_0)|dz\le 2\varepsilon\pi \end{aligned} ≤=∣∣∣∣∣∫∣z−z0∣=rz−z0f(z)dz−∫∣z−z0∣=rz−z0f(z0)dz∣∣∣∣∣∫∣z−z0∣=r∣z−z0∣∣f(z)−f(z0)∣dsr1∫∣z−z0∣=r∣f(z)−f(z0)∣dz≤2επ而 ∫ ∣ z − z 0 ∣ = r f ( z 0 ) z − z 0 d z = 2 π f ( z 0 ) i \int_{|z-z_0|=r}\frac{f(z_0)}{z-z_0}dz=2\pi f(z_0)i ∫∣z−z0∣=rz−z0f(z0)dz=2πf(z0)i于是 ∣ ∫ C f ( z ) z − z 0 d z − 2 i π f ( z 0 ) ∣ ≤ 2 π ε \left|\int_{C}\frac{f(z)}{z-z_0}dz-2i\pi f(z_0)\right|\le 2\pi \varepsilon ∣∣∣∣∫Cz−z0f(z)dz−2iπf(z0)∣∣∣∣≤2πε由 ε \varepsilon ε的任意性,就有 ∫ C f ( z ) z − z 0 d z = 2 π i f ( z 0 ) \int_{C}\frac{f(z)}{z-z_0}dz=2\pi if(z_0) ∫Cz−z0f(z)dz=2πif(z0)
解析函数的无穷可微性
定理5.6 f ( z ) f(z) f(z)在周线 C C C(单周线或复周线)围成的区域 D D D上解析, D ‾ \overline{D} D上连续,对任取的 z 0 ∈ D z_0\in D z0∈D, f ( z ) f(z) f(z)在 z 0 z_0 z0处有任意阶导数,并且有 f ( p ) ( z 0 ) = p ! 2 π i ∫ C f ( z ) ( z − z 0 ) p + 1 d z f^{(p)}(z_0)=\frac{p!}{2\pi i}\int_C \frac{f(z)}{(z-z_0)^{p+1}}dz f(p)(z0)=2πip!∫C(z−z0)p+1f(z)dz
证:
我们先看 p = 1 p=1 p=1的情形,考察 f ( z ) − f ( z 0 ) z − z 0 = 1 2 i π Δ z ∫ C [ f ( ξ ) ξ − z − f ( ξ ) ξ − z 0 ] d ξ = 1 2 i π Δ z ∫ C f ( ξ ) Δ z ( ξ − z ) ( ξ − z 0 ) d ξ = 1 2 i π ∫ C f ( ξ ) ( ξ − z ) ( ξ − z 0 ) d ξ \begin{aligned} &\frac{f(z)-f(z_0)}{z-z_0}=\frac{1}{2i\pi\Delta z}\int_C[\frac{f(\xi)}{\xi - z}-\frac{f(\xi)}{\xi - z_0}]d\xi\\ =&\frac{1}{2i\pi\Delta z}\int_C\frac{f(\xi)\Delta z}{(\xi-z)(\xi-z_0)}d\xi=\frac{1}{2i\pi}\int_C\frac{f(\xi)}{(\xi-z)(\xi-z_0)}d\xi \end{aligned} =z−z0f(z)−f(z0)=2iπΔz1∫C[ξ−zf(ξ)−ξ−z0f(ξ)]dξ2iπΔz1∫C(ξ−z)(ξ−z0)f(ξ)Δzdξ=2iπ1∫C(ξ−z)(ξ−z0)f(ξ)dξ而 ∫ C f ( ξ ) ( ξ − z ) ( ξ − z 0 ) d ξ − ∫ C f ( ξ ) ( ξ − z 0 ) 2 d ξ = Δ z ∫ C f ( ξ ) ( ξ − z ) ( ξ − z 0 ) 2 d ξ \begin{aligned} &\int_C\frac{f(\xi)}{(\xi-z)(\xi-z_0)}d\xi-\int_C\frac{f(\xi)}{(\xi-z_0)^2}d\xi\\ =&\Delta z\int_C\frac{f(\xi)}{(\xi-z)(\xi-z_0)^2}d\xi \end{aligned} =∫C(ξ−z)(ξ−z0)f(ξ)dξ−∫C(ξ−z0)2f(ξ)dξΔz∫C(ξ−z)(ξ−z0)2f(ξ)dξ由于 z 0 ∈ D z_0\in D z0∈D,存在 δ > 0 \delta>0 δ>0, B ‾ ( z 0 , δ ) ⊂ D \overline{B}(z_0,\delta)\subset D B(z0,δ)⊂D,当 Δ z < δ 2 \Delta z<\frac{\delta}{2} Δz<2δ时,见下图
其中 C n + 1 C_{n+1} Cn+1为 ∣ ξ − z 0 ∣ = δ |\xi-z_0|=\delta ∣ξ−z0∣=δ,方向沿逆时针,由柯西积分定理,有 ∣ ∫ C f ( ξ ) ( ξ − z ) ( ξ − z 0 ) 2 d ξ ∣ = ∣ ∫ C n + 1 f ( ξ ) ( ξ − z ) ( ξ − z 0 ) 2 d ξ ∣ ≤ ∫ C n + 1 ∣ f ( ξ ) ∣ ∣ ξ − z ∣ ∣ ξ − z 0 ∣ 2 d s = 1 δ 2 ∫ C n + 1 ∣ f ( ξ ) ∣ ∣ ξ − z ∣ d ξ \begin{aligned} &\left|\int_C\frac{f(\xi)}{(\xi-z)(\xi-z_0)^2}d\xi\right|=\left|\int_{C_{n+1}}\frac{f(\xi)}{(\xi-z)(\xi-z_0)^2}d\xi\right|\\ \le&\int_{C_{n+1}}\frac{|f(\xi)|}{|\xi-z||\xi-z_0|^2}ds=\frac{1}{\delta^2}\int_{C_{n+1}}\frac{|f(\xi)|}{|\xi-z|}d\xi \end{aligned} ≤∣∣∣∣∫C(ξ−z)(ξ−z0)2f(ξ)dξ∣∣∣∣=∣∣∣∣∫Cn+1(ξ−z)(ξ−z0)2f(ξ)dξ∣∣∣∣∫Cn+1∣ξ−z∣∣ξ−z0∣2∣f(ξ)∣ds=δ21∫Cn+1∣ξ−z∣∣f(ξ)∣dξ令 M M M为 ∣ f ( ξ ) ∣ |f(\xi)| ∣f(ξ)∣在 C n + 1 C_{n+1} Cn+1上的最大值,同时 ∣ ξ − z ∣ ≥ δ 2 |\xi-z|\ge\frac{\delta}{2} ∣ξ−z∣≥2δ,因此 1 δ 2 ∫ C n + 1 ∣ f ( ξ ) ∣ ∣ ξ − z ∣ d ξ ≤ 4 M π δ 2 \begin{aligned} &\frac{1}{\delta^2}\int_{C_{n+1}}\frac{|f(\xi)|}{|\xi-z|}d\xi\le \frac{4M\pi}{\delta^2} \end{aligned} δ21∫Cn+1∣ξ−z∣∣f(ξ)∣dξ≤δ24Mπ因此 lim z → z 0 ( ∫ C f ( ξ ) ( ξ − z ) ( ξ − z 0 ) d ξ − ∫ C f ( ξ ) ( ξ − z 0 ) 2 d ξ ) = lim z → z 0 Δ z ∫ C f ( ξ ) ( ξ − z ) ( ξ − z 0 ) 2 d ξ = 0 \begin{aligned} &\lim_{z\to z_0}(\int_C\frac{f(\xi)}{(\xi-z)(\xi-z_0)}d\xi-\int_C\frac{f(\xi)}{(\xi-z_0)^2}d\xi)\\ =&\lim_{z\to z_0}\Delta z\int_C\frac{f(\xi)}{(\xi-z)(\xi-z_0)^2}d\xi=0 \end{aligned} =z→z0lim(∫C(ξ−z)(ξ−z0)f(ξ)dξ−∫C(ξ−z0)2f(ξ)dξ)z→z0limΔz∫C(ξ−z)(ξ−z0)2f(ξ)dξ=0这就证得了 f ′ ( z 0 ) = 1 2 i π ∫ C f ( ξ ) ( ξ − z 0 ) 2 d ξ f^\prime(z_0)=\frac{1}{2i\pi}\int_C\frac{f(\xi)}{(\xi-z_0)^2}d\xi f′(z0)=2iπ1∫C(ξ−z0)2f(ξ)dξ其他阶导数可用数学归纳法类似证明,这里不再赘述
推论5.1 f ( x ) f(x) f(x)在区域 D D D上解析,则 f ( x ) f(x) f(x)在区域 D D D上有无穷阶导数
对于 z 0 ∈ D z_0\in D z0∈D,只要找一个闭邻域 B ‾ ( z 0 , δ ) ⊂ D \overline{B}(z_0,\delta)\subset D B(z0,δ)⊂D,其边界为 C : ∣ z − z 0 ∣ = δ C:|z-z_0|=\delta C:∣z−z0∣=δ,然后应用定理5.6即可。在数学分析中,在开区间 ( a , b ) (a,b) (a,b)上可导的函数不一定有无穷阶导数,而在复变函数中,在区域 D D D上可导的函数却有无穷阶导数,这是解析函数优良性质。
例5.4 通过计算 ∫ ∣ z ∣ = 1 ( z + 1 z ) 2 n d z z ( n = 1 , 2 , ⋯ ) \int_{|z|=1}(z+\frac{1}{z})^{2n}\frac{dz}{z}(n=1,2,\cdots) ∫∣z∣=1(z+z1)2nzdz(n=1,2,⋯)证明 ∫ 0 2 π cos 2 n θ d θ = 2 π ( 2 n − 1 ) ! ! ( 2 n ) ! ! \int_0^{2\pi}\cos^{2n}\theta d\theta = 2\pi \frac{(2n-1)!!}{(2n)!!} ∫02πcos2nθdθ=2π(2n)!!(2n−1)!!
证:令 f ( z ) = ( z 2 + 1 ) 2 n f(z)=(z^2+1)^{2n} f(z)=(z2+1)2n,我们先求 f ( 2 n ) ( z ) f^{(2n)}(z) f(2n)(z),由二项式定理 f ( z ) = ∑ k = 0 2 n C 2 n k z 2 k f(z)=\sum_{k=0}^{2n}C_{2n}^kz^{2k} f(z)=k=0∑2nC2nkz2k
则 f ( 2 n ) ( z ) = C 2 n n ( 2 n ) ! + . . . + C 2 n 2 n ( 4 n ) ( 4 n − 1 ) ⋯ ( 2 n + 1 ) z 2 n f^{(2n)}(z)=C_{2n}^n(2n)!+...+C_{2n}^{2n}(4n)(4n-1)\cdots(2n+1)z^{2n} f(2n)(z)=C2nn(2n)!+...+C2n2n(4n)(4n−1)⋯(2n+1)z2n故 f ( 2 n ) ( 0 ) = ( 2 n ) ! C 2 n n = ( 2 n ) ! ( 2 n ) ! ( n ! ) 2 f^{(2n)}(0)=(2n)!C_{2n}^n=(2n)!\frac{(2n)!}{(n!)^2} f(2n)(0)=(2n)!C2nn=(2n)!(n!)2(2n)!由定理5.6,有 f ( 2 n ) ( 0 ) = ( 2 n ) ! 2 π i ∫ ∣ z ∣ = 1 ( z + 1 z ) 2 n d z z f^{(2n)}(0)=\frac{(2n)!}{2\pi i}\int_{|z|=1}(z+\frac{1}{z})^{2n}\frac{dz}{z} f(2n)(0)=2πi(2n)!∫∣z∣=1(z+z1)2nzdz故 ∫ ∣ z ∣ = 1 ( z + 1 z ) 2 n d z z = 2 i π C 2 n n \int_{|z|=1}(z+\frac{1}{z})^{2n}\frac{dz}{z}=2i\pi C_{2n}^n ∫∣z∣=1(z+z1)2nzdz=2iπC2nn对 z = e i θ z=e^{i\theta} z=eiθ,有 z + 1 z = cos 2 θ + 1 + i sin 2 θ e i θ = 2 cos θ z+\frac{1}{z}=\frac{\cos 2\theta+1+i\sin 2\theta}{e^{i\theta}}=2\cos\theta z+z1=eiθcos2θ+1+isin2θ=2cosθ则 ∫ ∣ z ∣ = 1 ( z + 1 z ) 2 n d z z = 2 2 n i ∫ 0 2 π cos 2 n θ d θ \int_{|z|=1}(z+\frac{1}{z})^{2n}\frac{dz}{z}=2^{2n}i\int_0^{2\pi}\cos^{2n}\theta d\theta ∫∣z∣=1(z+z1)2nzdz=22ni∫02πcos2nθdθ就有 ∫ 0 2 π cos 2 n θ d θ = 2 π ( 2 n ) ! ( 2 n ) ! ! ( 2 n ) ! ! = 2 π ( 2 n − 1 ) ! ! ( 2 n ) ! ! \int_0^{2\pi}\cos^{2n}\theta d\theta=2\pi\frac{(2n)!}{(2n)!!(2n)!!}=2\pi\frac{(2n-1)!!}{(2n)!!} ∫02πcos2nθdθ=2π(2n)!!(2n)!!(2n)!=2π(2n)!!(2n−1)!!
例5.5 计算积分 ∫ ∣ z ∣ = 2 d z z 2 + 2 \displaystyle \int_{|z|=2}\frac{dz}{z^2+2} ∫∣z∣=2z2+2dz
解:任取一条围绕着 2 i \sqrt{2}i 2i,但不含 − 2 i -\sqrt{2}i −2i,且包含在 ∣ z ∣ < 2 |z|<2 ∣z∣<2内的简单闭曲线 C 1 C_1 C1,及一条围绕着 − 2 i -\sqrt{2}i −2i,包含在 ∣ z ∣ < 2 |z|<2 ∣z∣<2,且在 C 1 C_1 C1的外区域的简单闭曲线 C 2 C_2 C2,由柯西积分定理
∫ ∣ z ∣ = 2 d z z 2 + 2 = ∫ C 1 d z z 2 + 2 + ∫ C 2 d z z 2 + 2 \int_{|z|=2}\frac{dz}{z^2+2}=\int_{C_1}\frac{dz}{z^2+2}+\int_{C_2}\frac{dz}{z^2+2} ∫∣z∣=2z2+2dz=∫C1z2+2dz+∫C2z2+2dz分别计算 ∫ C 1 d z z 2 + 2 , ∫ C 2 d z z 2 + 2 \displaystyle\int_{C_1}\frac{dz}{z^2+2},\int_{C_2}\frac{dz}{z^2+2} ∫C1z2+2dz,∫C2z2+2dz:
∫ C 1 d z z 2 + 2 = ∫ C 1 d z ( z + 2 i ) ( z − 2 i ) \int_{C_1}\frac{dz}{z^2+2}=\int_{C_1}\frac{dz}{(z+\sqrt{2}i)(z-\sqrt{2}i)} ∫C1z2+2dz=∫C1(z+2i)(z−2i)dz由于 1 z + 2 i \frac{1}{z+\sqrt{2}i} z+2i1在 C 1 C_1 C1的内区域 D 1 D_1 D1解析, D 1 ‾ \overline{D_1} D1上连续,由柯西积分公式:
2 π i 2 2 i = 2 π 2 = ∫ C 1 d z z 2 + 2 \frac{2\pi i}{2\sqrt{2} i}=\frac{\sqrt{2}\pi}{2}=\int_{C_1}\frac{dz}{z^2+2} 22i2πi=22π=∫C1z2+2dz同理得到 ∫ C 2 d z z 2 + 2 = − 2 π 2 \int_{C_2}\frac{dz}{z^2+2}=-\frac{\sqrt{2}\pi}{2} ∫C2z2+2dz=−22π因此 ∫ ∣ z ∣ = 2 d z z 2 + 2 = 0 \int_{|z|=2}\frac{dz}{z^2+2}=0 ∫∣z∣=2z2+2dz=0
刘维尔定理及代数基本定理
由定理5.6,我们可以对解析函数的各阶导数进行估计。
定理5.7(柯西积分不等式) f ( z ) f(z) f(z)在区域 D D D上解析, z 0 ∈ D z_0\in D z0∈D, z 0 z_0 z0的闭邻域 B ‾ ( z 0 , R ) ⊂ D \overline{B}(z_0,R)\subset D B(z0,R)⊂D,则 ∣ f ( p ) ( z 0 ) ∣ ≤ p ! M R n |f^{(p)}(z_0)| \le \frac{p!M}{R^n} ∣f(p)(z0)∣≤Rnp!M其中 M M M为 ∣ f ( z ) ∣ |f(z)| ∣f(z)∣在 ∣ z − z 0 ∣ = R |z-z_0|=R ∣z−z0∣=R上的最大值
证:
由定理5.6,就有 f ( p ) ( z 0 ) = p ! 2 π i ∫ ∣ z − z 0 ∣ = R f ( z ) ( z − z 0 ) p + 1 d z f^{(p)}(z_0)=\frac{p!}{2\pi i}\int_{|z-z_0|=R}\frac{f(z)}{(z-z_0)^{p+1}}dz f(p)(z0)=2πip!∫∣z−z0∣=R(z−z0)p+1f(z)dz因此 ∣ f ( p ) ( z 0 ) ∣ ≤ p ! 2 π ∫ ∣ z − z 0 ∣ = R ∣ f ( z ) ∣ ∣ z − z 0 ∣ p + 1 d s = p ! 2 π R p + 1 ∫ ∣ z − z 0 ∣ = R ∣ f ( z ) ∣ d z ≤ p ! M 2 π R p + 1 ∫ ∣ z − z 0 ∣ = R d z = p ! M R n \begin{aligned} &|f^{(p)}(z_0)|\le\frac{p!}{2\pi}\int_{|z-z_0|=R}\frac{|f(z)|}{|z-z_0|^{p+1}}ds=\frac{p!}{2\pi R^{p+1}}\int_{|z-z_0|=R}|f(z)|dz\\ \le&\frac{p!M}{2\pi R^{p+1}}\int_{|z-z_0|=R}dz=\frac{p!M}{R^n} \end{aligned} ≤∣f(p)(z0)∣≤2πp!∫∣z−z0∣=R∣z−z0∣p+1∣f(z)∣ds=2πRp+1p!∫∣z−z0∣=R∣f(z)∣dz2πRp+1p!M∫∣z−z0∣=Rdz=Rnp!M
如果 f ( z ) f(z) f(z)在整个复平面上解析,则称 f ( z ) f(z) f(z)是整函数。由上面的不等式,就可以得出以下定理
定理5.8(刘维尔定理) 有界整函数必恒为一常数
证:
设 ∣ f ( z ) ∣ ≤ M |f(z)|\le M ∣f(z)∣≤M,任取一点 z ∈ C z\in C z∈C,由定理5.7,有 f ′ ( z ) ≤ M R f^\prime(z) \le \frac{M}{R} f′(z)≤RM 其中 R R R为任意的正数,令 R → ∞ R\to\infty R→∞,得到 f ′ ( z ) = 0 f^\prime(z)=0 f′(z)=0故 f ( z ) f(z) f(z)恒为常数
下面我们证明高等代数第一章提出的代数基本定理:
定理5.9(代数基本定理) 复 n n n次多项式( n ≥ 1 n\ge 1 n≥1)在复平面上必有零点
证:
对 n n n次多项式 p ( z ) = z n + a 1 z n − 1 + ⋯ + a n p(z)=z^n+a_1z^{n-1}+\cdots+a_n p(z)=zn+a1zn−1+⋯+an,如果 p ( z ) p(z) p(z)在 C C C上没有零点,那么存在 δ > 0 \delta>0 δ>0, p ( z ) ≥ δ p(z)\ge \delta p(z)≥δ,这是因为,首先 lim ∣ z ∣ → ∞ p ( z ) z n = 1 \lim_{|z|\to\infty}\frac{p(z)}{z^n}=1 ∣z∣→∞limznp(z)=1故 lim ∣ z ∣ → ∞ ∣ p ( z ) ∣ = ∞ \displaystyle\lim_{|z|\to\infty}|p(z)|=\infty ∣z∣→∞lim∣p(z)∣=∞,如果 inf z ∈ C p ( z ) = 0 \displaystyle \inf_{z\in C}p(z)=0 z∈Cinfp(z)=0,那么存在点列 { z n } \{z_n\} {zn},满足 lim n → ∞ ∣ p ( z n ) ∣ = 0 \displaystyle\lim_{n\to\infty}|p(z_n)|=0 n→∞lim∣p(zn)∣=0,存在 δ > 0 \delta>0 δ>0,当 ∣ z ∣ ≥ δ |z|\ge \delta ∣z∣≥δ时, ∣ p ( z ) ∣ ≥ 1 |p(z)|\ge 1 ∣p(z)∣≥1,存在 N N N, n ≥ N n\ge N n≥N时, ∣ p ( z n ) ∣ < 1 |p(z_n)|<1 ∣p(zn)∣<1,此时 ∣ z n ∣ < δ |z_n|<\delta ∣zn∣<δ。因此,存在 { z n } \{z_n\} {zn}的收敛子列 { z n k } \{z_{n_k}\} {