本文始发于个人公众号:TechFlow,原创不易,求个关注
今天是机器学习专题的第19篇文章,我们来看经典的Apriori算法。
Apriori算法号称是十大数据挖掘算法之一,在大数据时代威风无两,哪怕是没有听说过这个算法的人,对于那个著名的啤酒与尿布的故事也耳熟能详。但遗憾的是,随着时代的演进,大数据这个概念很快被机器学习、深度学习以及人工智能取代。即使是拉拢投资人的创业者也很少会讲到这个故事了,虽然时代的变迁令人唏嘘,但是这并不妨碍它是一个优秀的算法。

我们来简单回顾一下这个故事,据说在美国的沃尔玛超市当中,啤酒和尿布经常被摆放在同一个货架当中。如果你仔细观察就会觉得很奇怪,啤酒和尿布无论是从应用场景还是商品本身的属性来分都不应该被放在一起,为什么超市要这么摆放呢?
看似不合理的现象背后往往都有更深层次的原因,据说是沃尔玛引进了一种全新的算法,它分析了所有顾客在超市消费的记录,然后计算商品之间的关联性,发现这两件商品的关联性非常高。也就是说有大量的顾客会同时购买啤酒和尿布这两种商品,所以经过数据的分析,沃尔玛下令将这两个商品放在同一个货架上进行销售。果然这么一搞之后,两种商品的销量都提升了。
这个在背后分析数据,出谋划策充当军师一样决策的算法就是Apriori算法。
关联分析与条件概率
我们先把这个故事的真假放在一边,先来分析一下故事背后折射出来的信息。我们把问题进行抽象,沃尔玛超市当中的商品种类大概有数万种,我们的算法做的其实是根据售卖数据计算分析这些种类之间的相关性。专业术语叫做关联分析,这个从字面上很好理解。但从关联分析这个角度出发,我们会有些不一样的洞见。
我们之前都学过条件概率,我们是不是可以用条件概率来反应两个物品之间的关联性呢?比如,我们用A表示一种商品,B表示另外一种商品,我们完全可以根据所有订单的情况计算出P(A|B)和P(B|A),也就是说用户在购买了A的情况下会购买B的概率以及在购买B的情况下会购买A的概率。这样做看起来也很科学啊,为什么不这样做呢,还要引入什么新的算法呢?
这也就是算法必要性问题,这个问题解决不了,我们好像会很难说服自己去学习一门新的算法。其实回答这个问题很简单,就是成本。大型超市当中的商品一般都有几万种,而这几万种商品的销量差异巨大。一些热门商品比如水果、蔬菜的销量可能是冷门商品,比如冰箱、洗衣机的上千倍甚至是上万倍。如果我们要计算两两商品之间的相关性显然是一个巨大的开销,因为对于每两个商品的组合,我们都需要遍历一遍整个数据集,拿到商品之间共同销售的记录,从而计算条件概率。
我们假设商品的种类数是一万,超市的订单量也是一万好了,那么两两商品之间的组合就有一亿条,如果再乘上每次计算需要遍历一次整个数据集,那么整个运算的复杂度大概会是一万亿。如果再考虑多个商品的组合,那这个数字更加可怕。
但实际上一个大型超市订单量肯定不是万级别的,至少也是十万或者是百万量级甚至更多。所以这个计算的复杂度是非常庞大的,如果考虑计算带来的开销,这个问题在商业上就是不可解的。因为即使算出来结果带来的收益也远远无法负担付出的计算代价,这个计算代价可能比很多人想得大得多,即使是使用现成的云计算服务,也会带来极为昂贵的开销。如果考虑数据安全,不能使用其他公司的计算服务的话,那么自己维护这些数据和人工带来的消耗也是常人难以想象的。
如果想要得出切实可行的结果,那么优化算法一定是必须的,否则可能没有一家超市愿意付出这样的代价。
在我们介绍Apriori算法之前,我们可以先试着自己思考一下这个问题的解法。我真的试着想过,但是我没有得到很好的答案,对比一下Apriori算法我才发现,这并非是我个人的问题,而是因为我们的思维有误区。
如果你做过LeetCode,学过算法导论和数据结构,那么你在思考问题的时候,往往会情不自禁地从最优解以及最佳解的方向出发。反应在这个问题当中,你可能会倾向于找到所有高关联商品,或者是计算出所有商品对之间的关联性。但是在这个问题当中,前提可能就是错的。因为答案的完备性和复杂度之间往往是挂钩的,找出所有的答案必然会带来更多的开销,而且落实在实际当中,牺牲一些完备性也是有道理的。因为对于超市而言,更加关注高销量的商品,比如电冰箱和洗衣机,即使得出结论它们和某些商品关联性很高对超市来说也没有太大意义,因为电冰箱和洗衣机一天总共也卖不出多少台。
你仔细思考就会发现这个问题和算法的背景比我们一开始想的和理解的要深刻得多,所以让我们带着一点点敬畏之心来看看这个算法的详细吧。
频繁项集与关联规则
在我们具体了解算法的原理之前,我们先来熟悉两个术语。第一个属于叫做频繁项集,英文是frequent item sets。这个翻译很接地气,我们直接看字面意思应该就能理解。意思是经常会出现在一起的物品的集合。第二个属于叫做关联规则,也就是两个物品之间可能存在很强的关联关系。
用啤酒和尿布的故事举个例子,比如很多人经常一起购买啤酒和尿布,那么啤酒和尿布就经常出现在人们的购物单当中。所以啤酒和尿布就属于同一个频繁项集,而一个人买了啤酒很有可能还会购买尿布,啤酒和尿布之间就存在一个关联规则。表示它们之间存在很强的内在联系。
有了频繁项集和关联规则我们会做什么事情?很简单会去计算它们的概率。
对于一个集合而言,我们要考虑的是整个集合出现的概率。在这个问题场景当中,它的计算非常简单。即用集合当中所有元素一起出现的次数,除以所有的数据条数。这个概率也有一个术语,叫做支持度,英文称作support。
对于一个关联规则而言,它指的是A物品和B物品之间的内在关系,其实也就是条件概率。所以A->B关联规则的概率就是P(AB)/P(A)和条件概率的公式一样,不过在这个问题场景当中,也有一个术语,叫做置信度,英文是confidence。
其实confidence也好,support也罢,我们都可以简单地理解成出现的概率。这是一个计算概率的模型,可以认为是条件概率运算的优化。其中关联规则是基于频繁项集的,所以我们可以先把关联规则先放一放,先来主要看频繁项集的求解过程。既然频繁项集的支持度本质上也是一个概率,那么我们就可以使用一个阈值来进行限制了。比如我们规定一个阈值是0.5,那么凡是支持度小于0.5的集合就不用考虑了。我们先用这个支持度过一遍全体数据,找出满足支持度限制的单个元素的集合。之后当我们寻找两个元素的频繁项集的时候,它的候选集就不再是全体商品了,而只有那些包含单个元素的频繁项集。
同理,如果我们要寻找三项的频繁项集,它的候选集就是含有两项元素的频繁项集,以此类推。表面上看,我们是把候选的范围限制在了频繁项集内从而简化了运算。其实它背后有一个很深刻的逻辑,即不是频繁项集的集合,一定不可能构成其他的频繁项集。比如电冰箱每天的销量很低,它和任何商品都不可能构成频繁项集。这样我们就可以排除掉所有那些不是频繁项集的所有情况,大大减少了运算量。
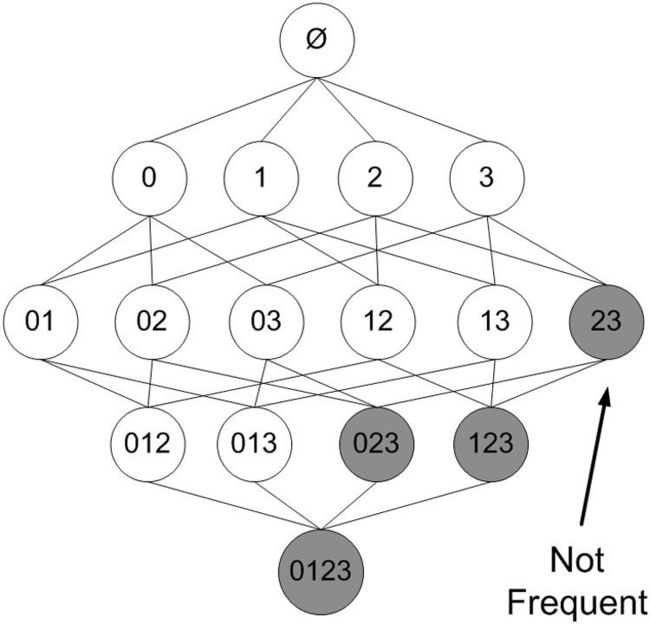
上图当中的23不是频繁项集,那么对应的123和023显然也都不是频繁项集。其实我们把这些非频繁的项集去掉,剩下的就是频繁项集。所以我们从正面或者是反面理解都可以,逻辑的内核是一样的。
Apriori算法及实现
其实Apriori的算法精髓就在上面的表述当中,也就是根据频繁项集寻找新的频繁项集。我们整理一下整个算法的流程,然后一点点用代码来实现它,对照代码和流程很容易就搞清楚了。
首先,我们来创建一批假的数据用来测试:
def create_dataset():
return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
下面我们要生成只有一个项的所有集合。这一步很好理解,我们需要对所有有交易的商品生成一个清单,也就是将所有交易记录中的商品购买记录进行去重。由于我们生成的结果在后序会作为dict的key,并且我们知道set也是可变对象,也是不可以作为dict中的key的。所以我们要做一点转换,将它转换成frozenset,它可以认为是不可以修改的set。
def individual_components(dataset):
ret = []
for data in dataset:
for i in data:
ret.append((i))
# 将list转化成set即是去重操作
ret = set(ret)
return [frozenset((i, )) for i in ret]
执行过后,我们会得到这样一个序列:
[frozenset({1}), frozenset({2}), frozenset({3}), frozenset({4}), frozenset({5})]
上面的这个序列是长度为1的所有集合,我们称它为C1,这里的C就是component,也就是集合的意思。下面我们要生成的f1,也就是长度为1的频繁集合。频繁集合的选取是根据最小支持度过滤的,所以我们下面要实现的就是计算Ck中每一个集合的支持度,然后过滤掉那些支持度不满足要求的集合。这个应该也很好理解:
def filter_components_with_min_support(dataset, components, min_support):
# 我们将数据集中的每一条转化成set
# 一方面是为了去重,另一方面是为了进行集合操作
dataset = list(map(set, dataset))
# 记录每一个集合在数据集中的出现次数
components_dict = defaultdict(int)
for data in dataset:
for i in components:
# 如果集合是data的子集
# 也就是data包含这个集合
if i <= data:
components_dict[i] += 1
rows = len(dataset)
frequent_components = []
supports = {}
for k,v in components_dict.items():
# 支持度就是集合在数据集中的出现次数除以数据总数
support = v / rows
# 保留满足支持度要求的数据
if support >= min_support:
frequent_components.append(k)
supports[k] = support
return frequent_components, supports
我们将支持度设置成0.5来执行一下,会得到以下结果:
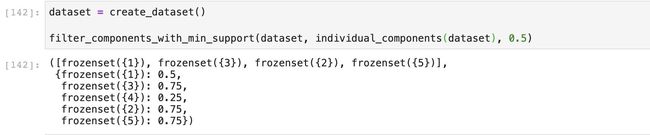
可以发现数据中的4被过滤了,因为它只出现了1次,支持度是0.25,达不到我们设置的阈值,和我们的预期一致。
现在我们有了方法创建长度为1的项集,也有了方法根据支持度过滤非频繁的项集,接下来要做的已经很明显了,我们要根据长度为1的频繁项集生成长度为2的候选集,然后再利用上面的方法过滤得到长度为2的频繁项集,再通过长度为2的频繁项集生成长度为3的候选集,如此往复,直到所有的频繁项集都被挖掘出来为止。
根据这个思路,我们接下来还有两个方法要做,一个是根据长度为n的频繁项集生成长度n+1候选集的方法,另一个方法是利用这些方法挖掘所有频繁项集的方法。
我们先来看根据长度为n的项集生成n+1候选集的方法,这个也很好实现,我们只需要用所有元素依次加入现有的集合当中即可。
def generate_next_componets(components):
# 获取集合当中所有单个的元素
individuals = individual_components(components)
storage = set()
for i in individuals:
for c in components:
# 如果i已经在集合中了则跳过
if i <= c:
continue
cur = i | c
# 否则合并,加入存储
if cur not in storage:
storage.add(cur)
return list(storage)
这些方法都有了之后,剩下的就很好办了,我们只需要重复调用上面的方法,直到找不到更长的频繁项集为止。我们直接来看代码:
def apriori(dataset, min_support):
# 生成长度1的候选集合
individuals = individual_components(dataset)
# 生成长度为1的频繁项集
f1, support_dict = filter_components_with_min_support(dataset, individuals, min_support)
frequent = [f1]
while True:
# 生成长度+1的候选集合
next_components = generate_next_componets(frequent[-1])
# 根据支持度筛选出频繁项集
components, new_dict = filter_components_with_min_support(dataset, next_components, min_support)
# 如果筛选结果为空,说明不存在更长的频繁项集了
if len(components) == 0:
break
# 更新结果
support_dict.update(new_dict)
frequent.append(components)
return frequent, support_dict
最后,我们运行一下这个方法查看一下结果:
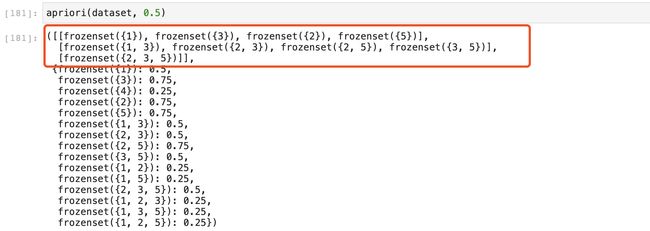
红色框中就是我们从数据集合当中挖掘出的频繁项集了。在一些场景当中我们除了想要知道频繁项集之外,可能还会想要知道关联规则,看看哪些商品之间存在隐形的强关联。我们根据类似的思路可以设计出算法来实现关联规则的挖掘。
关联规则
理解了频繁项集的概念之后再来算关联规则就简单了,我们首先来看一个很简单的变形。由于我们需要计算频繁项集之间的置信度,也就是条件概率。我们都知道P(A|B) = P(AB) / P(B),这个是条件概率的基本公式。这里的P(A) = 出现A的数据条数/ 总条数,其实也就是A的支持度。所以我们可以用支持度来计算置信度,由于刚刚我们在计算频繁项集的时候算出了所有频繁项集的支持度,所以我们可以用这份数据来计算置信度,这样会简单很多。
我们先来写出置信度的计算公式,它非常简单:
def calculate_confidence(comp, subset, support_dict):
return float(support_dict[comp]) / support_dict[comp-subset]
这里的comp表示集合,subset表示我们要推断的项。也就是我们挖掘的是comp-item这个集合与subset集合之间的置信度。
接着我们来看候选规则的生成方法,它和前面生成候选集合的逻辑差不多。我们拿到频繁项集之后,扣除其中的一个子集,将它作为一个候选的规则。
def generate_rules(components, subset):
all_set = []
# 生成所有子集,也就是长度更小的频繁项集的集合
for st in subset:
all_set += st
rules = []
# 遍历所有子集
for i in all_set:
# 遍历频繁项集
for comp in components:
# 如果子集关系成立,则生成了一条候选规则
if i <= comp:
rules.append((comp, i))
return rules
最后,我们把上面两个方法串联在一起,先生成所有的候选规则,再根据置信度过滤掉符合条件的关联规则。利用之前频繁项集时候生成的数据,很容易实现这点。
def mine_rules(frequent, support_dict, min_confidence):
rules = []
# 遍历长度大于等于2的频繁项集
for i in range(1, len(frequent)):
# 使用长度更小的频繁项集作为自己,构建候选规则集
candidate_rules = generate_rules(frequent[i], frequent[:i])
# 计算置信度,根据置信度进行过滤
for comp, item in candidate_rules:
confidence = calculate_confidence(comp, item, support_dict)
if confidence >= min_confidence:
rules.append([comp-item, item, confidence])
return rules
我们运行一下这个方法,看一下结果:
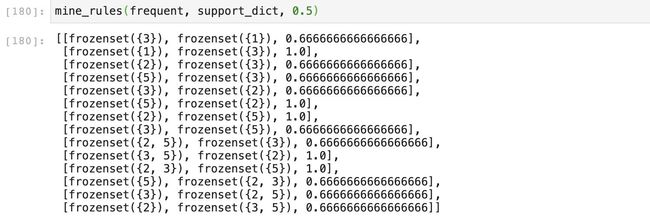
从结果来看还不错,我们挖掘出了所有的关联规则。要注意一点A->B和B->A是两条不同的规则,这并不重复。举个简单的例子,买乒乓拍的人往往都会买乒乓球,但是买乒乓球的人却并不一定会买乒乓拍,因为乒乓拍比乒乓球贵得多。而且乒乓球是消耗品,乒乓拍不是。所以乒乓拍可以关联乒乓球,但反之不一定成立。
结尾、升华
到这里,Apriori算法和它的应用场景就讲完了。这个算法的原理并不复杂,代码也不困难,没有什么高深的推导或者是晦涩的运算,但是算法背后的逻辑并不简单。怎么样为一个复杂的场景涉及简单的指标?怎么样缩小我们计算的范围?怎么样衡量数据的价值?其实这些并不是空穴来风,显然算法的设计者是付出了大量思考的。
如果我们顺着解法出发去试着倒推当时设计者的思考过程,你会发现看似简单的问题背后其实并不简单,看似自然而然的道理,也并不自然,这些看似寻常的背后都隐藏着逻辑,这些背后的思考和逻辑,才是算法真正宝贵的部分。
今天的文章就到这里,原创不易,需要你的一个关注,你的举手之劳对我来说很重要。
