两种智能小车的建模与仿真

1.两种智能小车的构造简介

在市面上常见的两种智能小车都是基于轮式的，在某宝上面卖的最多的，各位在学生时代拿来应付课程设计和毕业设计用的各种小车分为两种。
1.后轮驱动，前轮阿克曼转向的，通常后轴通过有刷直流电机驱动，前轴通过舵机带动连杆转向。英文通常称为Car-like Model.
2.差速驱动，这种最为多见，可以做成轮式的，也可以做成履带式的。通过每个轮子都有电机，当然你可以说成为轮毂电机驱动。这种通常称为Tank-like Model.
通过在分析控制问题的时候，第一步就是需要对被控对象进行数学模型的建立，这里我们不强调模型的复杂性，因为大多数都在低速情况行驶，所以可以只考虑运动学模型，如果您需要参加XXX智能车比赛，这类竞速类的项目，就必须考虑动力学模型，且需要通过大量的试验对模型进行参数估计和辨识。本次只谈论简易的运动学模型，并且进行Simulink环境的模型搭建，最后通过一个仿真环境来验证模型的可用性！

2.需要的软件与硬件

1.电脑一台
2.装有Matlab/Simulink的软件
本次只在仿真环境中建模，不需要小车的硬件和控制器硬件。

3. Car-like小车建模与仿真

3.1 模型推导

先给大家一个直观的印象，如在我的上一篇博客中的小车就属于Car-like 小车。您可以跳回上一篇文章进行查看小车图片。
那么对于小车研究运动学模型，是需要对其简化的，可以简化成如下图所示的模型。如果您不想看数学推导，可以直接看最后的推导结果。
假设小车的重心坐标(x,y)，则后轮中心坐标为(x1,y1)，前轮中心坐标为(x2,y2)。 $\theta$为方位角，即与x轴的正方向的夹角。$\psi$为前轮转角。
那么后轮的位置关系如下：
$$\begin{gathered} x_1=x-b\ast cos\theta \\ {y}_{{}_1}=y-b\ast sin\theta \end{gathered}$$
对上式求微分，后轮的速度：
$$\begin{gathered} \dot{x_1}=\dot{x}+b\ast \dot{\theta }\ast sin\theta \\ \dot{y_1}=\dot{y}-b\ast \dot{\theta }\ast cos\theta \end{gathered}$$
假设后轮无侧滑（约束）：
$$\begin{gathered} \frac{\dot{y_1}}{\dot{x_1}}=\frac{sin\theta }{cos\theta } \\ \frac{\dot{y}-b\ast \dot{\theta }\ast cos\theta }{\dot{x}+b\ast \dot{\theta }\ast sin\theta }=\frac{sin\theta }{cos\theta } \end{gathered}$$
将上式化简，可以得出后轮对质心约束的运动方程
$$\dot{x}sin\theta -\dot{y}cos\theta +b\dot{\theta }=0\left(1\right)$$
同样分析前轮，可得前轮位置关系：
$$\begin{gathered} x_2=x+a\ast cos\theta \\ {y}_{{}_2}=y+a\ast sin\theta \end{gathered}$$
对上式求微分，前轮的速度：
$$\begin{gathered} \dot{x_2}=\dot{x}-a\ast \dot{\theta }\ast sin\theta \\ \dot{y_2}=\dot{y}+a\ast \dot{\theta }\ast cos\theta \end{gathered}$$
同样对前轮进行约束，假设没有侧滑，满足如下约束,其中 $\psi$为前轮转角：
$$\frac{\dot{y_2}}{\dot{x_2}}=\frac{sin\left(\theta +\psi \right)}{cos\left(\theta +\psi \right)}$$
将前轮的速度公式代入，可得前轮对质心运动的约束方程：
$$\dot{x}sin\left(\theta +\psi \right)-\dot{y}cos\left(\theta +\psi \right)-a\dot{\theta }cos\psi =0\left(2\right)$$
定义小车前进方向Longitudinal的速度为$V_u$，小车的侧向速度Lateral（法向）$V_w$，那么根据上图可以得如下关系式,十分简单的三角关系运算：
$$\begin{gathered} \dot{x}=v_u\ast cos\theta -v_w\ast sin\theta \\ \dot{y}=v_u\ast sin\theta +v_w\ast cos\theta \left(3\right) \end{gathered}$$
将（1）式代入（3）式，也就是将约束代入,一通计算化简。可得：
$$v_w=b\dot{\theta }$$
将（2）式代入（3）式，一通化简，可得：
$$\dot{\theta }=\frac{v_u}{L}tan\left(\psi \right)$$
看似小车的运动方程就计算出来了。
$$\begin{gathered} \dot{x}=v_{u}cos\theta -b\dot{\theta }sin\theta \\ \dot{y}=v_{u}sin\theta +b\dot{\theta }cos\theta \\ \dot{\theta }=\frac{v_u}{L}tan\left(\psi \right) \end{gathered}$$
不过使用后轮中心(x1,y1)表示小车位置会更简单,将后轮的速度方程代入上式，便可得到最终的运动学模型：
$$\begin{gathered} \dot{x}=vcos\theta \\ \dot{y}=vsin\theta \\ \dot{\theta }=\frac{v}{L}tan\left(\psi \right) \end{gathered}$$
其中v是小车轴向速度，x,y代表小车后轴中心点的大地坐标。

3.2 Simulink模型搭建

首先，根据上节中的内容搭建仿真模型，具体模型如下图所示，如果您才入门Simulink，可以按照我的模型自己动手建一遍。

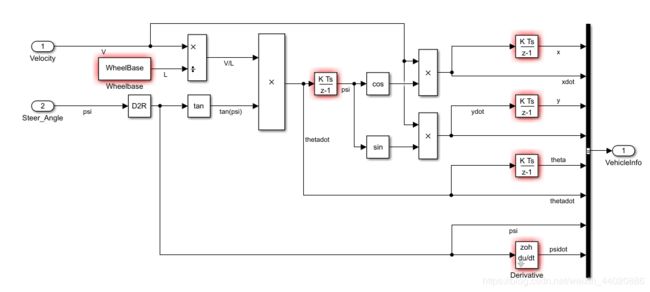
您会问我为什么会报错呢，原因很简单，我并没有在Baseworkspace或者数据字典定义参数的具体数值，所示编译器无法识别具体参数，为什么我这么做呢，因为会将这部分模型封装成子系统。在子系统封装界面输入参数。具体报错原因我点进去几个模块给您看一下。例如这个积分模块

这个模块输出值代表小车的大地坐标中的横坐标，在Initial Condition中是定义小车的初始值，这里通过参数定义小车的初始横坐标，采样时间用参数表示方便自定义采样时间，不用每次都打开模型输入。其他方位角，纵坐标，轴距其实都是一样的。输出模块我用了Bus模块，也是方便我们查看自己感兴趣的输出信号。接下来封装子系统。全选界面，右键选择Create Subsystem from Selection。如下图所示，可以看到，还是存在报错情况，不过没关系，稍后会进行解决。车身系统目前就建立完了。

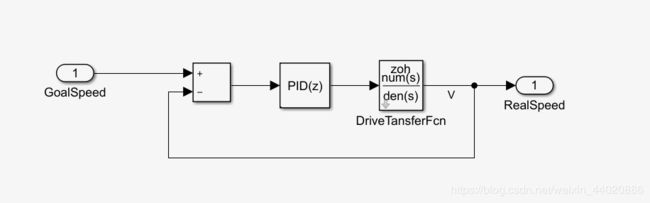
然后我们将进行转向系统和驱动系统的建立，驱动系统的建立我就不用示意了，在上一篇博客中我已经详细说明了驱动系统的模型是如何建立的，这时只需要把上次的模型拿过来，接入速度接口就可以了。输入：期望车速。输出：实际速度。当然控制器不属于系统本身的模型，这里我为了后期方便仿真，就放在一起了。

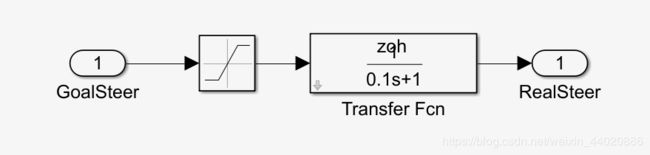
那么转向系统的模型如何建立呢？小车使用的是一个舵机，舵机具有非常大的惯性，如果用过的同学肯定都知道，这里我使用一个一阶惯性环节来表示转向系统，一阶惯性环节的滞后这里我就不做详细的数学推导了，从bode图上可以看相位有90度的滞后。这里就用一个开环控制，因为转向舵机我目前无法通过传感器进行反馈控制。时间常数tao的选取决定了系统滞后时间。不过注意不要将惯性环节和延迟环节进行混淆，千万需要注意！其中Saturation模块是对小车的期望转角做一个限制的，限制最大转角，在模块中输入参数MaxSteerAngle，后期进行封装使用。

如果您不确定滞后参数，可以加个Scope看一下滞后的时间，从而选定时间常数tao。这时我们将整个系统表示为如下图所示。

软件的架构一定要清晰，这是最基本的!
接下来创建一个整体的子系统。

在VehicleBody子系统里，参数没有定义还是处于报错状态。那么右键子系统，选择Mask->Create Mask，出现下图界面：

先选中Parameters，再点击左侧的Edit。编辑成如下图所示：

其中name对应您设置的参数名字，Prompt对应您在封装界面显示的名字。并且您可以在Documentation条目中进行子系统的描述。最后点击Ok。再次点击您的子系统，可见已经封装完成。

当然您也可以右键子系统Mask->Add Icon Image选择您小车的图片，我也将自己的小车图片加上去了。并且您可以在Library中将您的模型生成自定义库。这里我就不展示具体怎么做了，搜索引擎可以找到很多教程！您也可以私信我，我会指导您进行自定义模块的搭建。

3.3 Car-like小车模型仿真

本次的仿真环境我使用Mathworks培训视频提供的一个demo，在此demo上进行修改，这个demo的需求是：通过规划好路径，设计纯追踪控制器，使小车能够良好的跟踪轨迹！模型我在官方的例子上进行了修改（第一部分是用脚本文件重写），非原版。但是架构没有改变。

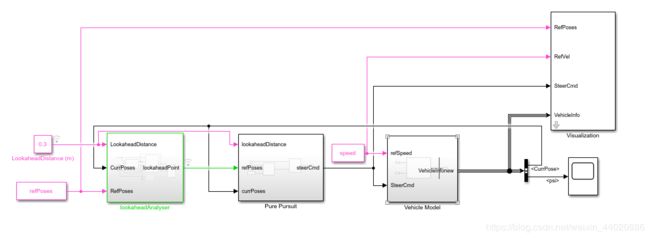
demo中分为三个部分，第一个部分是寻找预瞄点，通过对车辆反馈的当前位置和参考路径位置进行计算，第二部分就是控制器算法，具体算法这里我就不解释了，在CSDN搜索纯跟踪您可以看到关于此类车辆模型详细的控制器数学推导。第三部分就是车辆模型部分了
从图可以看到这个demo使用的Powertrain Blockset工具箱中的3dof自行车动力学模型。我们需要将此模型替换成我们刚刚建立好的模型用我们的模型进行仿真，其他参数一律不进行修改。

已经替换完成，设置小车参数以及车辆在坐标系初始位置。其中SignalProcess子系统里是信号的处理。



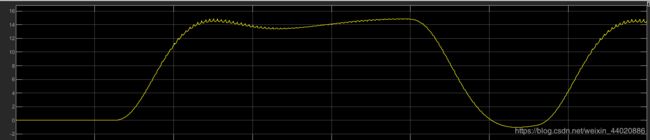
这时点击仿真。红色点是小车的实际路径，参考路径是蓝色的，可以明显看到，小车在预瞄距离0.3米的情况下，跟踪的很好。和官方的二自由度小车动力学模型结果几乎误差，这里我就没有把两者的误差进行对比了，大家可以看下轨迹效果。说明基于运动学建立的模型在低速环境下使用是没有问题的。

前轮转角也十分平稳，这里我用的离散模型，采用时间是5e3秒，官方提供的模型是连续的，只不过它在后面的信号处理用了RateTransition模块。

4.Tank-like小车建模与仿真

4.1 模型推导

Tank-like小车模型较前者简单，并且在某宝的普及率是远远高于带前轮转向的小车的，因为价格相对便宜很多，通过用两块亚克力板和四个轮子加香蕉电机就可以完成组装。下图即为小车简化后的模型。

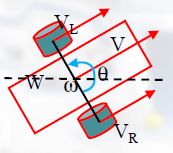
从图中可以看出，$V_L$和$V_R$分别代表小车的左轮和右轮的前进速度，$W$代表轮距，$\theta$代表方位角，和前一个模型一样，即与x轴正方向的夹角（也有仿真软件定义为与y轴正方向的夹角）。$w$即绕Z轴的横摆角速度（转向的角速度，因为是绕质心进行转向的），单位$rad/s$。不难得出如下结论，做一个简单的几何学的分析。
$$\begin{gathered} V=\frac{1}{2}(V_L+V_R) \\ w=(V_R-V_L))/W \end{gathered}$$
$$\begin{gathered} \dot{x}=V\ast cos\theta \\ \dot{y}=V\ast sin\theta \\ \dot{\theta }=w \end{gathered}$$
运动学关系就非常清晰了，可以通过速度和角速度求解出x与y的位置，也可以求解出左右的速度分别是多少。那么下一步就可以在Simulink中建模了。

4.2 Simulink模型搭建

建模也十分简单，将上面推导的公式代入，就可以得到一系列的输出了，这里我输出了8个值，分别是小车的x和y的位置信息，x和y的速度信息，方位角和角速度信息和两个车辆不同的前进速度！

注意在高亮的模块中，是需要和上个模型一样在模块中定义初始值和采样时间的，最后用总线信号输出。然后按照上一个模型类似步骤的简单封装，就可以做成如下图所示的样子。

当您需要输出什么信号的时候，后接一个Bus Selector即可选择您想要的任何信号。

4.3 控制器推导

那么如何搭建一个仿真环境呢，官方提供的例子中是阿克曼转向的前轮小车控制器设计，我们现在需要一个差速小车的纯跟踪控制器，没有轮子就需要自己从头造轮子了，那就先从原理入手吧。都是非常简单基于几何的控制算法，所以有图形就可以直观的通过数学关系解析出控制器表达式。

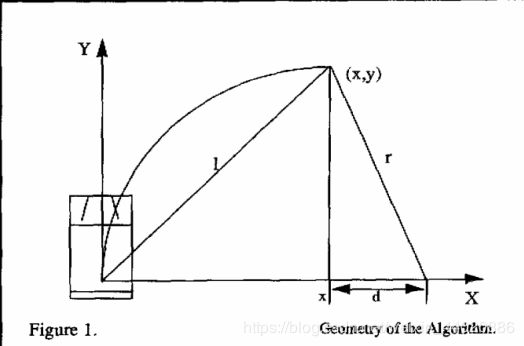
图片和推导公式节选自论文[1]
根据几何关系可以推导、一系列数学关系式。
$$\begin{gathered} x^2+y^2=l^2 \\ x+d=r \\ d=r-x \\ (r-x{)}^2+y^2=r^2 \\ {r}^2-2rx+x^2+y^2=r^2 \\ 2rx=l^2 \\ r=\frac{l^2}{2x} \\ \gamma =\frac{2x}{l^2} \end{gathered}$$
其中$r$和$\gamma$分别代入目标点（x,y）的半径和曲率，$l$表示差速小车的预瞄距离。可以看出这类似P控制器，输出为$\gamma$，输入为$xoffset$。最终的控制律为：
$$\gamma =\frac{2x}{l^2}$$
当然您可以发现我们需要的距离 $x$是在小车坐标系下的，而预瞄距离是在大地坐标系下的，所以在求出预瞄点坐标的时候，您需要将预瞄点坐标转换到小车的坐标系中，而坐标系按如下方法进行转换的：
（1）首先将预瞄点坐标平移到以小车坐标为原点的坐标系中。
（2）将平移后的坐标系旋转小车的方位角$\theta$，得到最终的小车坐标系。

4.4 仿真环境搭建

参考轨迹按照上个模型的仿真环境不变，计算预瞄点距离的算法子系统不变，我们需要改变的是控制器子系统和车辆模型子系统。

当然在MAAB建模规范中，是尽量避免模块和子系统出现在同一层的，除非必要模块，这里我为了让大家看清原理，就直接把乘法器放在外面了。请务必记住如下公式，大多数人可能对高中物理有些淡忘。
$$w=\frac{v}{r}=v\ast \gamma$$
再看控制器如何设计的，最重要的就是坐标系的转换（蓝色区域），建议有兴趣的同学可以自己推算一遍，十分简单的数学几何关系。这里就没有使用参考轨迹的方位角信息了！

整体模型架构如下。

本次仿真设置的是预瞄距离20cm，车速0.5m/s，开始仿真。看一下期望轨迹。

这是差速小车，当然您可以将左轮速度和右轮速度输出看一下。总体来说弄懂原理十分简单。参数的具体值就不对比了。如果您有兴趣可以从头自己搭建一个您自己期望的参考轨迹，根据已经设计好的控制器进行仿真看一下效果。将x和y坐标接入xyGraph模块一样可以看到实际轨迹。

5.总结

本次进行了两种常见的小车模型推导，建模与仿真，其中Tank-like小车您也可以沿用成履带式的小车，在低速有约束的情况下都是模型都是通用的。当您从某宝等电商平台购买回一台小车，我建议您从小车的构造本质进行入手，才能最其进行更好的控制，控制首先需要对被控对象进行深入的了解，无论是正向原则和数据驱动的方式建模，都需要对模型进行搭建，才能展开后续控制器的设计。
如果您使用的是Matlab2019b，那您可以在机器人工具箱中找到我今天做的两种小车模型和差速小车纯跟踪控制器，区别在于工具箱中的模块是基于面向对象编程的方法，没有用Simulink模块搭建，底层代码是不可见的。您可以验证下本次教程的模型搭建是否和官方的模型有出入。

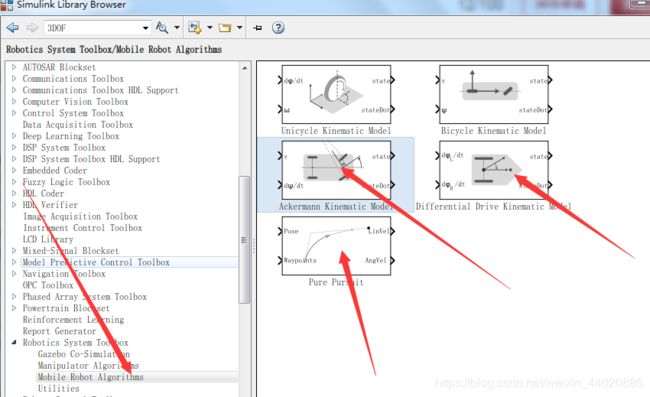
我们不但需要Know-How，而且需要Know-Why！

如果您对本次仿真的模型感兴趣，可以在评论区留下您的邮箱或者私信，我会发送至您的邮箱，如果版本低于2018a，请留言备注。

参考文献

[1] Coulter, R. Implementation of the Pure Pursuit Path Tracking Algorithm. Carnegie Mellon University, Pittsburgh, Pennsylvania, Jan 1990.