HOJ.12931 ZZ

ZZ

Problem description

ZZ-function, a shorter name of ZeedZaad-function is defines as followed.

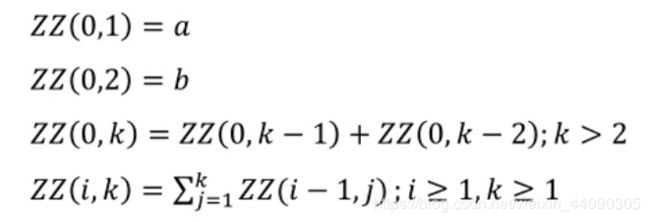
Given 4 inegers a, b, c and d, your task is to find ZZ(c, d)

Input

First line of input is a number of test cases T ≤ 200.

Each test case is a line containing of 4 integers a, b, c and d (0 ≤ a, b ≤ 1 000 000 000, 1 ≤ c ≤ 100, 1 ≤ c x d ≤ 100 000 000)

Output

For each test case, display ZZ(c, d) mod 1 000 000 009.

Sample Input

5
1 1 1 1
1 1 1 4
1 1 2 3
1 1 5 5
24995 8633 1 25158567

Sample Output

1
7
7
155
512203519

Problem Source

2013 ACM-ICPC Thailand National Programming Contest

为了写这篇博客还是花了不少功夫, 因为今天写博客发现沙雕百度输入法输进markdown直接崩（之前还好端端的，今天突然出问题了）。（也许是沙雕markdown）
不管为什么

直接把他卸了，看到都烦

进入正题：

 这是一个推广的类似Fibonacci序列的数列。第一行其实就是一个Fibonacci数列，我们知道Fibonacci数列可以用快速幂解决，从前往后递推，那么我们考虑这道题是不是也可以用矩阵快速幂呢？手动列举了几个例子，试图发现规律

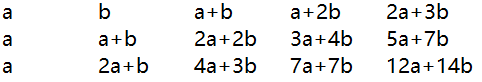
如果暴力推的话，时间是O(c*d)的。无法接受。因此不能直接计算。

思路1(超时)：
我们可以推出第一行，然后根据运用组合数求解要求的项：
如要求ZZ（1，4）（第二行第四个，行从0，开始，列从1开始）
我们可以发现，ZZ（1，4）由第一行中的第一个4+第一行中的第二个3+第一行中的第三个2+第一行中的第4个1
所以只需要第一行中的前四个乘以一个向量（4，3，2，1）T即可
因此我们只需要找到这个向量
不难推出这其实是一个斜着的杨辉三角，用组合数可以解决。
因为这是一个超时的算法，不做过多解释，组合数也很好推，先上错误代码：

package DailyCode;

import java.io.*;
import java.util.StringTokenizer;
import static ACMProblem.ACMIO.*;

public class LiuJuanFibonacci {

    static int MOD = 1000000009;

    public static long combination(long n, long m, int mod) {
        //make it as small as possible
        if (m > n - m)
            m = n - m;
        if (m == 0)
            return 1;
        long fz = 1, fm = 1;
        for (int i = 1; i <= m; i++) {
            fz = (fz * (n - i + 1)) % mod;
            fm = (fm * i) % mod;
        }
        long fmInv = fastPow(fm, mod - 2, mod);
        return (fz * fmInv) % mod;
    }

    public static long fastPow(long a, long n, long M) {
        long r = 1, base = a;
        while (n != 0) {
            //if is odd
            if ((n & 1) != 0)
                r = r * base % M;
            base = base * base % M;
            n >>= 1;
        }
        return r % M;
    }

    static long getYH(int r, int c) {
        if (r < 0 || c < 0)
            return 1;
        return combination((long) (r + c), (long) c, MOD);
    }

    public static void main(String[] args) throws Exception {
        setStream(System.in);
        int n = nextInt();
        long res = 0;
        int[] fibonacci;
        for (int i = 0; i < n; ++i) {
            res = 0;
            int a = nextInt();
            int b = nextInt();
            int c = nextInt();
            int d = nextInt();
            --c;
            long foo = a;
            long bar = b;
            long foobar;
            res += getYH(c, d - 1) * a;
            if (d > 1)
                res += getYH(c, d - 2) * b;
            for (int j = 3; j <= d; ++j) {
                foobar = foo + bar;
                foobar = foobar % MOD;
                foo = bar;
                bar = foobar;
                res += (getYH(c, d - j) % MOD) * foobar;
                res %= MOD;
            }
            out.println(res);
            out.flush();
        }
    }
}


 */

思路二(超时):
我们可以通过第一列，通过一系列的加法运算，推出第二列，这就变成了一个矩阵快速幂的问题，十分简单。复杂度为$O(c^3\log d)$, 由于样例过多，如果直接这样做，这是依然超时的。。。原理简单，不再赘述，超时的部分核心代码：

	
    static MatrixLong generateMatrix(int n) {
        long[][] data = new long[n][n];
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j)
                if (i >= j)
                    data[i][j] = 1;
        data[0][0] = 0;
        data[0][1] = 1;
        return new MatrixLong(data);
    }

    static MatrixLong generateVector(int a, int b, int n) {
        assert n > 2;
        long[][] data = new long[n][1];
        data[0][0] = a;
        data[1][0] = b;
        for (int i = 2; i < n; ++i)
            data[i][0] = ((i - 1) * a % MOD + b) % MOD;
        return new MatrixLong(data);
    }

    static long solve(int a, int b, int c, int d) {
        if (d == 1)
            return a;
        else if (d == 2)
            return (a * c + b) % MOD;
        else {
            vec = generateVector(a, b, c + 2);
            MatrixLong mat = generateMatrix(c + 2);
            return mat.pow(d - 2, MOD).dot(vec, MOD).getData()[c + 1][0];
        }
    }

思路3(AC):
我们可以算出要求的项是由多少个a和b组成的。
同样的，某列中的各项有多少个a和多少个b相加而成（后简称为a的个数和b的个数）可以由前一列经过加法运算得到，和思路一类似，由于记录的是个数，而不是具体的a，b值，因此具有普适性，可以先大致的打表，每个样例都可以用打好的结果，来乘a或乘b。就不需要每次都对大矩阵做大量的幂运算。还有一个点就是，对于大矩阵未必快速幂就快，有的时候乘以一个小矩阵，缩小规模可能效果更好。

对于小数据，可以直接用思路一的方法，小矩阵快速幂效果良好。
对于大矩阵就可以先打表，用通用的方法计算a和b的个数来得到结果
不难计算，当临界值为30左右时效率最佳
AC代码：

/*
 * Copyright (c) 2019 Ng Kimbing, HNU, All rights reserved. May not be used, modified, or copied without permission.
 * @Author: NgKimbing College of Computer Scienceand Electronic Engineering Hunan University.
 * @LastModified:2019-06-10 T 14:06:59.061 +08:00
 */
package DailyCode;

import java.io.*;
import java.util.StringTokenizer;
import MyUtil.MatrixLong;

import static ACMProblem.ACMIO.*;

public class LiuJuanFibonacci2 {
  
    private static final int MOD = 1000000009;
    private static final int MAX_CD = 100000000;
    private static final int BLOCK_SIZE = 1000;
    private static final int C_THRESHOLD = 30;
    private static final int SIZE = MAX_CD / C_THRESHOLD / BLOCK_SIZE + 5;
    // the second column
    private static MatrixLong vec; // [a, b, a+b, 2a+b, 3a+b ...]T
    private static MatrixLong mat;
    private static MatrixLong table;

    private static MatrixLong generateMatrix(int n) {
        long[][] data = new long[n][n];
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j)
                if (i >= j)
                    data[i][j] = 1;
        data[0][0] = 0;
        data[0][1] = 1;
        return new MatrixLong(data);
    }

    private static MatrixLong generateVector(int a, int b, int n) {
        assert n > 2;
        long[][] data = new long[n][1];
        data[0][0] = a;
        data[1][0] = b;
        for (int i = 2; i < n; ++i)
            data[i][0] = ((i - 1) * a % MOD + b) % MOD;
        return new MatrixLong(data);
    }

    private static void makeTable() {
        int size = 105;
        long[][] data = new long[size][1];
        for (int i = 0; i < size; ++i)
            data[i][0] = i;
        data[0][0] = 1;
        vec = new MatrixLong(data);
        mat = generateMatrix(size);
        mat = mat.pow(BLOCK_SIZE, MOD);
        long[][] tab = new long[SIZE][size];
        for (int j = 0; j < size; ++j)
            tab[0][j] = j;
        tab[0][0] = 1;
        for (int i = 1; i < SIZE; ++i) {
            vec = mat.dot(vec, MOD);
            long[][] bar = vec.getData();
            for (int j = 0; j < size; ++j)
                tab[i][j] = bar[j][0];
        }
        table = new MatrixLong(tab);
    }

    private static void getNextColumn(long[] arr) {
        long temp = arr[1];
        arr[1] = (arr[0] + arr[1]) % MOD;
        arr[0] = temp;
        for (int i = 2; i < arr.length; ++i)
            arr[i] = (arr[i] + arr[i - 1]) % MOD;
    }

    private static long solve(int a, int b, int c, int d) {
        if (d == 1)
            return a;
        if (d == 2)
            return (a * c + b) % MOD;
        if (c < C_THRESHOLD) {
            vec = generateVector(a, b, c + 2);
            MatrixLong mat = generateMatrix(c + 2);
            return mat.pow(d - 2, MOD).dot(vec, MOD).getData()[c + 1][0];
        } else {
            int pos = (d - 3) / BLOCK_SIZE;
            long[][] tab = table.getData();
            long[] bar = new long[tab[pos].length];
            System.arraycopy(tab[pos], 0, bar, 0, tab[pos].length);
            int remainder = (d - 3) % BLOCK_SIZE;
            for (int i = 0; i < remainder; ++i)
                getNextColumn(bar);
            long n2 = bar[c + 1];
            getNextColumn(bar);
            long n1 = bar[c];
            return (n1 * a % MOD + n2 * b % MOD) % MOD;
        }
    }

    public static void main(String[] args) throws Exception {
        setStream(System.in);
        makeTable();
        int n = nextInt();
        for (int i = 0; i < n; ++i) {
            int a = nextInt();
            int b = nextInt();
            int c = nextInt();
            int d = nextInt();
            out.println(solve(a, b, c, d));
            out.flush();
        }
    }
}
/*
5
1 1 1 1
1 1 1 4
1 1 2 3
1 1 5 5
24995 8633 1 25158567

 */

思路4
其实以上方法还是太笨，OJ上博士 0ms AC， 一定还有什么更强的算法，应该涉及很多数学知识。有机会向他请教请教再来完善思路4