一、数据预处理:数值型特征无量纲化
1.数据标准化(Standardization)
标准化的前提是特征值服从正态分布,标准化后,其转换成标准正态分布。
优点:
Z-Score最大的优点就是简单,容易计算,Z-Score能够应用于数值型的数据,并且不受数据量级的影响,因为它本身的作用就是消除量级给分析带来的不便。
缺点:
估算Z-Score需要总体的平均值与方差,但是这一值在真实的分析与挖掘中很难得到,大多数情况下是用样本的均值与标准差替代;
Z-Score对于数据的分布有一定的要求,正态分布是最有利于Z-Score计算的;
Z-Score消除了数据具有的实际意义,A的Z-Score与B的Z-Score与他们各自的分数不再有关系,因此Z-Score的结果只能用于比较数据间的结果,数据的真实意义还需要还原原值;
在存在异常值时无法保证平衡的特征尺度。
2.归一化
1)MinMax归一化
区间缩放法利用了边界值信息,将属性缩放到[0,1]。
缺点:这种方法有一个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义;MinMaxScaler对异常值的存在非常敏感。
(2) MaxAbs归一化
单独地缩放和转换每个特征,使得训练集中的每个特征的最大绝对值将为1.0,将属性缩放到[-1,1]。它不会移动/居中数据,因此不会破坏任何稀疏性
缺点:这种方法有一个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义;MaxAbsScaler与先前的缩放器不同,绝对值映射在[0,1]范围内。
在仅有正数据时,该缩放器的行为MinMaxScaler与此类似,因此也存在大的异常值。
3.正态分布化(Normalization)
正则化的过程是将每个样本缩放到单位范数(每个样本的范数为1),如果要使用如二次型(点积)或者其它核方法计算两个样本之间的相似性这个方法会很有用。
该方法是文本分类和聚类分析中经常使用的向量空间模型(Vector Space Model)的基础。Normalization主要思想是对每个样本计算其p-范数,然后对该样本中每个元素除以该范数,这样处理的结果是使得每个处理后样本的p-范数(l1-norm,l2-norm)等于1。
4.标准化与归一化对比
1)标准化与归一化的异同
相同点:
它们的相同点在于都能取消由于量纲不同引起的误差;都是一种线性变换,都是对向量X按照比例压缩再进行平移。
不同点:
目的不同,归一化是为了消除纲量压缩到[0,1]区间;
标准化只是调整特征整体的分布;
归一化与最大,最小值有关;
标准化与均值,标准差有关;
归一化输出在[0,1]之间;
标准化无限制。
2)什么时候用归一化?什么时候用标准化?
如果对输出结果范围有要求,用归一化;
如果数据较为稳定,不存在极端的最大最小值,用归一化;
如果数据存在异常值和较多噪音,用标准化,可以间接通过中心化避免异常值和极端值的影响。
3)归一化与标准化的应用场景
在分类、聚类算法中,需要使用距离来度量相似性的时候(如SVM、KNN)、或者使用PCA技术进行降维的时候,标准化(Z-score standardization)表现更好;
在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用第一种方法或其他归一化方法。
比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围;
基于树的方法不需要进行特征的归一化。
例如随机森林,bagging与boosting等方法。
如果是基于参数的模型或者基于距离的模型,因为需要对参数或者距离进行计算,都需要进行归一化。
二、数值型特征特征分箱(数据离散化)
离散化是数值型特征非常重要的一个处理,其实就是要将数值型数据转化成类别型数据。连续值的取值空间可能是无穷的,为了便于表示和在模型中处理,需要对连续值特征进行离散化处理。
分箱的重要性及其优势:
离散特征的增加和减少都很容易,易于模型的快速迭代;
稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
离散化后的特征对异常数据有很强的鲁棒性;
比如一个特征是年龄>30是1,否则0。
如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰;
对于线性模型,表达能力受限;
单变量离散化为N个后,每个变量有单独的权重,相当于模型引入了非线性,能够提升模型表达能力,加大拟合;
离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;特征离散化后,模型会更稳定;
比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。
当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问;
特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险;
可以将缺失作为独立的一类带入模型;将所有变量变换到相似的尺度上。
1.无监督分箱法
1)自定义分箱
自定义分箱,是指根据业务经验或者常识等自行设定划分的区间,然后将原始数据归类到各个区间中。
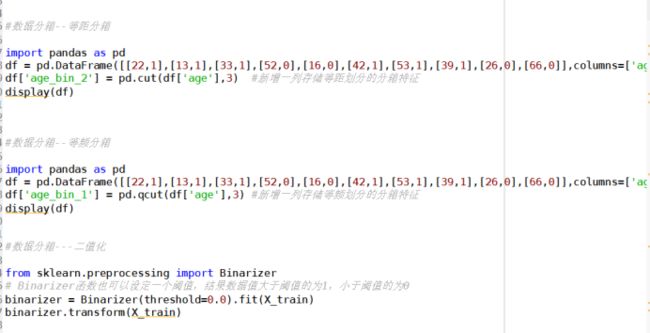
2)等距分箱
按照相同宽度将数据分成几等份。
[if !supportLists]3)[endif]等频分箱
将数据分成几等份,每等份数据里面的个数是一样的。区间的边界值要经过选择,使得每个区间包含大致相等的实例数量。比如说 N=10 ,每个区间应该包含大约10%的实例。
4)聚类分箱
5)二值化(Binarization)
2.有监督分箱法(忽略)
三、总结
1)特征预处理是数据预处理过程的重要步骤,是对数据的一个的标准的处理,几乎所有的数据处理过程都会涉及该步骤。
2)我们对特征进行分箱后,需要对分箱后的每组(箱)进行woe编码和IV值的计算,通过IV值进行变量筛选后,然后才能放进模型训练。
3)分箱后需要进行特征编码,如:LabelEncode、OneHotEncode或LabelBinarizer等。
实践代码: