权值线段树/主席树学习笔记+例题

介绍

以下转自：大佬
还有知乎有一篇比较好的介绍： 浅谈权值线段树到主席树

前言

据说主席树这个名字的由来呢，是因为创始人的名字缩写hjt与某位相同，然后他因为不会划分树于是自创了这一个数据结构。好强啊orz

主席树能实现什么操作呢？最经典的就是查询区间第k小了，其他的还有诸如树上路径第k小啦，带修改第k小啦之类的。以静态区间第k小为例

定义

先贴一下某神犇对主席树的理解：所谓主席树呢，就是对原来的数列[1…n]的每一个前缀[1…i]（1≤i≤n）建立一棵线段树，线段树的每一个节点存某个前缀[1…i]中属于区间[L…R]的数一共有多少个（比如根节点是[1…n]，一共i个数，sum[root] = i；根节点的左儿子是[1…(L+R)/2]，若不大于(L+R)/2的数有x个，那么sum[root.left] = x）。若要查找[i…j]中第k大数时，设某结点x，那么x.sum[j] - x.sum[i - 1]就是[i…j]中在结点x内的数字总数。而对每一个前缀都建一棵树，会MLE，观察到每个[1…i]和[1…i-1]只有一条路是不一样的，那么其他的结点只要用回前一棵树的结点即可，时空复杂度为O(nlogn)。

然而没有什么用，因为感觉根本没看懂

然后来说说我自己的理解吧。如何求出一个区间内第k小呢？直接sort当然可以，但是复杂度爆表。于是我们可以换一个思路，能否将[l,r]之间出现过的数都建成线段树呢？设节点为p，区间为[l,r]，左儿子是[l,mid]，右儿子是[mid+1,r]
要查找第k大的话，先看左儿子里有多少个数（表示小于等于mid的数的个数），如果大于k，进左子树找，否则令k−=左儿子数的个数，进右子树找

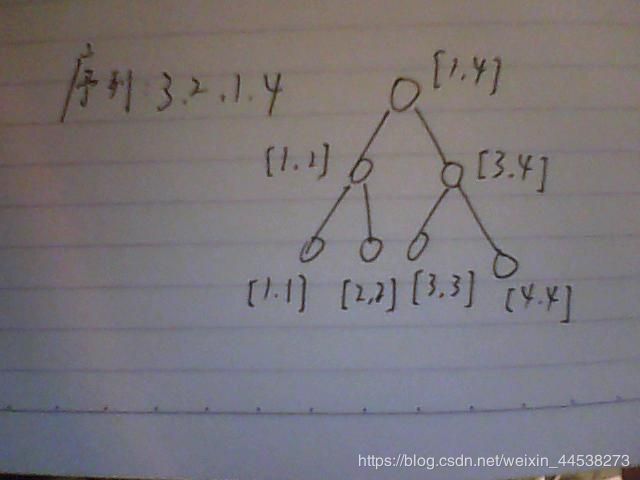
先来考虑一个序列：3,2,1,4

建完树之后是这样的

然后要查第2大，一下子就能发现是2了

（上面画的可能不是很严谨，大家将就下）

但我们不可能对每一个区间都建一棵树，那样的话空间复杂度绝对爆炸

然后可以转化一下思路：前缀和

区间[l,r]中小于等于mid的数的个数，可以转换为[1,r]中小于等于mid的数的个数减去[1,l−1]中小于等于mid的数的个数

于是我们只要对每一个前缀建一棵树即可

然后空间复杂度还是爆炸

然而我们又发现，区间[1,l−1]的树和区间[1,l]的树最多只会有logn个节点不同（因为每次新插入一个节点最多只会更新logn个节点），有许多空间是可以重复利用的

只要能将这些空间重复利用起来，就可以解决空间的问题了

还是上面那个序列：3，2,1,4

一开始先建一棵空树，然后一个个把每一个节点加进去

如果要看图的话可以点这里

这个时候有人就要问了，万一序列的数字特别大呢？

当然是离散化

将这些所有值离散一下就行了，可以保证所有数在1 n之间

然而感觉讲太多也没啥用……上代码好了，有详细的注释

例题

模板

Zoo
Description
JZ拥有一个很大的野生动物园。这个动物园坐落在一个狭长的山谷内，这个区域从南到北被划分成N个区域，每个区域都饲养着一头狮子。这些狮子从北到南编号为1,2,3,…,N。每头狮子都有一个觅食能力值Ai，Ai越小觅食能力越强。饲养员西西决定对狮子进行M次投喂，每次投喂都选择一个区间[I,J]，从中选取觅食能力值第K强的狮子进行投喂。值得注意的是，西西不愿意对某些区域进行过多的投喂，他认为这样有悖公平。因此西西的投喂区间是互不包含的(即区间[1,10]不会与[3,4]或[5,10]同时存在，但可以与[9,11]或[10,20]一起)。同一区间也只会出现一次。你的任务就是算出每次投喂后，食物被哪头狮子吃掉了。

Input
第一行，两个整数N,M。

第二行，N个整数Ai。(1 ≤ Ai ≤ 2^31-1)$。

此后M行，每行描述一次投喂。第t+2行的三个数I,J,K表示在第t次投喂中，西西选择了区间[I,J]内觅食能力值第K强的狮子进行投喂。

Output
输出文件有M行，每行一个整数。第i行的整数表示在第i次投喂中吃到食物的狮子的觅食能力值。

Sample Input
7 2
1 5 2 6 3 7 4
1 5 3
2 7 1
Sample Output
3
2
Data Constraint
对于100%的数据，有1 ≤ N ≤ 10^5,1 ≤ M ≤ 5 × 10^4。

来源
JZOJ

Analysis 分析
可持久化线段树/主席树
主席树的主要思想就是：保存每次插入操作时的历史版本，以便查询区间第$k$小。

怎么保存呢？暴力一点，每次开一棵线段树呗。

那空间还不爆掉？

那么我们分析一下，发现每次修改操作修改的点的个数是一样的。

（例如下图，修改了[1,8]中对应权值为1的结点，红色的点即为更改的点）

只更改了log(n)个结点，形成一条链，也就是说每次更改的结点数 = 树的高度。

注意主席树不能使用堆式存储法，就是说不能用x × 2,x × 2 + 1来表示左右儿子，而是应该动态开点，并保存每个节点的左右儿子编号。

所以我们只要在记录左右儿子的基础上存一下插入每个数的时候的根节点就可以持久化辣。

我们把问题简化一下：每次求[1,r]区间内的k小值。

怎么做呢？只需要找到插入r时的根节点版本，然后用普通权值线段树做就行了，如果不会用普通权值线段树做的话请参见开头部分的解释。

那么这个相信大家很简单都能理解，把问题扩展到原问题——求[l,r]区间k小值。

这里我们再联系另外一个知识理解：前缀和。

它运用了区间减法的性质，通过预处理从而达到O(1)回答每个询问。

那么我们主席树也行！如果需要得到[l,r]的统计信息，只需要用[1,r]的信息减去[1,l - 1]的信息就行了（请好好地想一想是不是如此）

那么至此，该问题解决！（完结撒花）

关于空间问题，我们分析一下：由于我们是动态开点的，所以一棵线段树只会出现2n-1个结点。然后，有n次修改，每次增加log(n)个结点。那么最坏情况结点数会达到2n-1+nlog(n)，那么此题的n ≤ 10^5，通过计算得到$log{2}^{(10^5)}$≈17，那么把n和log的结果代入这个式子，变成$2\times 10^5-1+17\times 10^5$，忽略掉-1，大概就是19 × 10^5。

算了这么一大堆，I tell you: 千万不要吝啬空间！保守一点，直接上个2^5 × 10^5 = 32 × 10^5，接近原空间的两倍（即n << 5）。

（较真的同学请注意，如果你真的很吝啬，可以自己造个数据输出一下结点数量，但是如果数据没造好把自己卡掉了就尴尬了）

P.S: 实测该题需要开到20n+10个结点，19n+10会Wonderful Answer 80pts，该程序对于N = 10^5的数据开到了1968911个结点，大于19n+10。
代码：

#include 
#include 
#include 
using namespace std;
const int maxn = 1e5;//数据范围
int tot,n,m;
int sum[(maxn << 5) + 10],rt[maxn + 10],ls[(maxn << 5) + 10],rs[(maxn << 5) + 10];
int a[maxn + 10],ind[maxn + 10],len;
inline int getid(const int &val)//离散化
{
    return lower_bound(ind + 1,ind + len + 1,val) - ind;
}
int build(int l,int r)//建树
{
    int root = ++tot;
    if(l == r)
        return root;
    int mid = l + r >> 1;
    ls[root] = build(l,mid);
    rs[root] = build(mid + 1,r);
    return root;//返回该子树的根节点
}
int update(int k,int l,int r,int root)//插入操作
{
    int dir = ++tot;
    ls[dir] = ls[root],rs[dir] = rs[root],sum[dir] = sum[root] + 1;
    if(l == r)
        return dir;
    int mid = l + r >> 1;
    if(k <= mid)
        ls[dir] = update(k,l,mid,ls[dir]);
    else
        rs[dir] = update(k,mid + 1,r,rs[dir]);
    return dir;
}
int query(int u,int v,int l,int r,int k)//查询操作
{
    int mid = l + r >> 1,x = sum[ls[v]] - sum[ls[u]];//通过区间减法得到左儿子的信息
    if(l == r)
        return l;
    if(k <= x)//说明在左儿子中
        return query(ls[u],ls[v],l,mid,k);
    else//说明在右儿子中
        return query(rs[u],rs[v],mid + 1,r,k - x);
}
inline void init()
{
    scanf("%d%d",&n,&m);
    for(register int i = 1;i <= n;++i)
        scanf("%d",a + i);
    memcpy(ind,a,sizeof ind);
    sort(ind + 1,ind + n + 1);
    len = unique(ind + 1,ind + n + 1) - ind - 1;
    rt[0] = build(1,len);
    for(register int i = 1;i <= n;++i)
        rt[i] = update(getid(a[i]),1,len,rt[i - 1]);
}
int l,r,k;
inline void work()
{
    while(m--)
    {
        scanf("%d%d%d",&l,&r,&k);
        printf("%d\n",ind[query(rt[l - 1],rt[r],1,len,k)]);//回答询问
    }
}
int main()
{
    init();
    work();
    return 0;
}

权值线段树例题

Weight Tarot 权值塔罗牌
Description 题目描述
最近小L收集了一套塔罗牌，每个塔罗牌上面有一个权值，不超过10^5，现有N个操作，分别有以下三种情况：

Add x 如果当前的手牌中没有权值为x的塔罗牌则加入，否则忽略该操作。
Remove x 如果当前的手牌中有权值为x的塔罗牌则弃掉该牌，否则忽略该操作。
Query 查询当前手牌中权值最接近的两张牌的权值之差，如果当前手牌数量少于2张牌，输出-1。
Input Format 输入格式
第一行，一个整数 N。

接下来 N 行，每行一个操作。

Output Format 输出格式
对于每个Query操作，输出一行，表示操作的结果。

Sample 样例
Sample Input 样例输入
12
Add 1
Remove 2
Add 1
Query
Add 7
Query
Add 10
Query
Add 5
Query
Remove 7
Query
Sample Output 样例输出
-1
6
3
2
4
Data Constraint 数据范围
N ≤ 10^5

Source 来源
改编自学校OJ一题

Analysis 分析
注意，对于各个操作的描述，可以看出塔罗牌的权值不能重复！

那么，就可以构造一棵根节点区间为[1,10^5]的线段树，在树上乱搞，这就是权值线段树的核心思想——（划重点）以数据范围为区间进行答案的维护（这句话是自己说的说错了别打我（逃）

大概是这样的：

对于每个结点，我们维护三个值：min,max,diff，分别代表区间最小值，区间最大值，区间最小差。

递归维护的时候，

min=min{lson.min,rson.min},max=max{lson.max,rson.max}

这个不难理解，但是最小差呢……

思考一下，容易发现更新的时候有三种状态： - 左儿子$[l,mid]$区间维护的最小差

右儿子[mid + 1,r]区间维护的最小差
右儿子区间维护的最小值与左儿子区间维护的最大值的差
然后对于三种情况，min一下就可以了（注意左儿子和右儿子都可能没有数，这时就需要去除对应的情况）

一个技巧：建树的时候可以把最小值初始化为正无穷，把最大值初始化为负无穷，这样更新最小差的时候只需要对第三种状态判断左右最值是否为无穷即可，因为对无穷作min是无用的。

代码：

#include 
#include 
#include 
#define lson (root << 1)
#define rson (lson | 1)
using namespace std;
int n,x;
char opt[15];
struct node
{
    int l,r;
    int max,min,diff;
} seg[400010];
void build(int l,int r,int root = 1)//初始建树操作
{
    seg[root].min = seg[root].diff = 0x3f3f3f3f;
    seg[root].max = -0x3f3f3f3f;
    seg[root].l = l,seg[root].r = r;
    //以上初值不多说
    if(l == r)
        return ;
    int mid = l + r >> 1;
    build(l,mid,lson);
    build(mid + 1,r,rson);
}
void generate(int x,int root = 1)//加牌操作
{
    if(seg[root].l == seg[root].r)
    {
        seg[root].max = seg[root].min = x;
        return ;
    }
    int mid = seg[root].l + seg[root].r >> 1;
    if(x <= mid)
        generate(x,lson);
    if(x > mid)
        generate(x,rson);
    seg[root].max = max(seg[lson].max,seg[rson].max);
    seg[root].min = min(seg[lson].min,seg[rson].min);
    if(seg[lson].max == -0x3f3f3f3f || seg[rson].min == 0x3f3f3f3f)
        seg[root].diff = min(seg[lson].diff,seg[rson].diff);
    else
        seg[root].diff = min(seg[rson].min - seg[lson].max,min(seg[lson].diff,seg[rson].diff));
}
void remove(int x,int root = 1)//弃牌操作
{
    if(seg[root].l == seg[root].r)
    {
        seg[root].max = -0x3f3f3f3f;
        seg[root].min = 0x3f3f3f3f;
        return ;
    }
    int mid = seg[root].l + seg[root].r >> 1;
    if(x <= mid) 
        remove(x,lson);
    if(x > mid)
        remove(x,rson);
    seg[root].max = max(seg[lson].max,seg[rson].max);
    seg[root].min = min(seg[lson].min,seg[rson].min);
    if(seg[lson].max == -0x3f3f3f3f || seg[rson].min == 0x3f3f3f3f)
        seg[root].diff = min(seg[lson].diff,seg[rson].diff);
    else
        seg[root].diff = min(seg[rson].min - seg[lson].max,min(seg[lson].diff,seg[rson].diff));
}
int main()
{
    scanf("%d",&n);
    build(1,100000);//数据范围
    while(n--)
    {
        scanf("%s",opt);
        if(!strcmp(opt,"Add"))
        {
            scanf("%d",&x);
            generate(x);
        }
        else if(!strcmp(opt,"Remove"))//else if减少多余的strcmp调用
        {
            scanf("%d",&x);
            remove(x);
        }
        else if(!strcmp(opt,"Query"))
            printf("%d\n",seg[1].diff == 0x3f3f3f3f ? -1 : seg[1].diff);//注意判断-1情况
    }
}

以区间第k小为例 洛谷p3834

代码：

//minamoto
#include
#define N 200005
using namespace std;
inline int read(){
    #define num ch-'0'
    char ch;bool flag=0;int res;
    while(!isdigit(ch=getchar()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getchar());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
int sum[N<<5],L[N<<5],R[N<<5];
int a[N],b[N],t[N];
int n,q,m,cnt=0;
int build(int l,int r){
    int rt=++cnt;
    //建树 
    sum[rt]=0;
    if(l<r){
        int mid=(l+r)>>1;
        L[rt]=build(l,mid);
        R[rt]=build(mid+1,r);
    }
    return rt;
}
int update(int last,int l,int r,int x){
    int rt=++cnt;
    L[rt]=L[last],R[rt]=R[last],sum[rt]=sum[last]+1;
    //先继承上一次的信息 
    //L是左节点，R是右节点，sum是节点内数的个数 
    if(l<r){
        int mid=(l+r)>>1;
        if(x<=mid) L[rt]=update(L[last],l,mid,x);
        else R[rt]=update(R[last],mid+1,r,x);
        //如果有需要更新的信息，更新
        //可以发现每一次更新的节点最多只有log n个 
    }
    return rt;
}
int query(int u,int v,int l,int r,int k){
    if(l>=r) return l;
    int x=sum[L[v]]-sum[L[u]];
    //查询操作 
    int mid=(l+r)>>1;
    if(x>=k) return query(L[u],L[v],l,mid,k);
    else return query(R[u],R[v],mid+1,r,k-x);
    //如果左节点个数大于等于k，进左子树找第k小
    //否则进右子树 
}
int main(){
    //freopen("testdata.in","r",stdin);
    n=read(),q=read();
    for(int i=1;i<=n;++i)
    b[i]=a[i]=read();
    sort(b+1,b+1+n);
    m=unique(b+1,b+1+n)-b-1;
    t[0]=build(1,m);
    //先建一棵空树 
    for(int i=1;i<=n;++i){
        int k=lower_bound(b+1,b+1+m,a[i])-b;
        //离散 
        t[i]=update(t[i-1],1,m,k);
        //然后每次在上一次的基础上建树 
    }
    while(q--){
        int x,y,z;
        x=read(),y=read(),z=read();
        int k=query(t[x-1],t[y],1,m,z);
        printf("%d\n",b[k]);
    }
    return 0;
}

如果熟练了之后，可以发现其实第一步的建树过程是可以省略的，直接每一步加节点就行了

//minamoto
#include
#define N 200005
using namespace std;
inline int read(){
    #define num ch-'0'
    char ch;bool flag=0;int res;
    while(!isdigit(ch=getchar()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getchar());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
int sum[N<<5],L[N<<5],R[N<<5];
int a[N],b[N],t[N];
int n,q,m,cnt=0;
void update(int last,int &now,int l,int r,int x){
    //注意这里开的是引用 
    if(!now) now=++cnt;
    sum[now]=sum[last]+1;
    if(l==r) return;
    int mid=(l+r)>>1;
    if(x<=mid) R[now]=R[last],update(L[last],L[now],l,mid,x); // 往哪走更新哪一路
    else L[now]=L[last],update(R[last],R[now],mid+1,r,x);
}
int query(int u,int v,int l,int r,int k){
    if(l>=r) return l;
    int x=sum[L[v]]-sum[L[u]];
    int mid=(l+r)>>1;
    if(x>=k) return query(L[u],L[v],l,mid,k);
    else return query(R[u],R[v],mid+1,r,k-x);
}
int main(){
    //freopen("testdata.in","r",stdin);
    n=read(),q=read();
    for(int i=1;i<=n;++i)
    b[i]=a[i]=read();
    sort(b+1,b+1+n);
    m=unique(b+1,b+1+n)-b-1;
    for(int i=1;i<=n;++i){
        int k=lower_bound(b+1,b+1+m,a[i])-b;  //这里插入的是权值
        update(t[i-1],t[i],1,m,k); // 因为now是引用格式的，所以这里t[i]的值会自动更新
        //省略建树过程，直接加入节点 
    }
    while(q--){
        int x,y,z;
        x=read(),y=read(),z=read();
        int k=query(t[x-1],t[y],1,m,z);
        printf("%d\n",b[k]);
    }
    return 0;
}

给一个数列，每次询问一个区间内有没有一个数出现次数超过一半

主席树的一般应用 洛谷P3567 [POI2014]KUR-Couriers
出现次数可以转化为左右节点的大小，如果符合条件就递归

//minamoto
#include
#define N 500005
using namespace std;
inline int read(){
    #define num ch-'0'
    char ch;bool flag=0;int res;
    while(!isdigit(ch=getchar()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getchar());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
int sum[N*20],L[N*20],R[N*20],t[N];
int n,q,cnt=0;
void update(int last,int &now,int l,int r,int x){
    if(!now) now=++cnt;
    sum[now]=sum[last]+1;
    if(l==r) return;
    int mid=(l+r)>>1;
    if(x<=mid) R[now]=R[last],update(L[last],L[now],l,mid,x);
    else L[now]=L[last],update(R[last],R[now],mid+1,r,x);
}
int query(int u,int v,int l,int r,int k){
    if(l==r) return l;
    int x=sum[L[v]]-sum[L[u]],y=sum[R[v]]-sum[R[u]];
    int mid=(l+r)>>1;
    if(x*2>k) return query(L[u],L[v],l,mid,k);
    if(y*2>k) return query(R[u],R[v],mid+1,r,k);
    return 0;
}
int main(){
    //freopen("testdata.in","r",stdin);
    n=read(),q=read();
    for(int i=1;i<=n;++i){
        int x=read();
        update(t[i-1],t[i],1,n,x);
    }
    while(q--){
        int x,y;
        x=read(),y=read();
        int k=query(t[x-1],t[y],1,n,y-x+1);
        printf("%d\n",k);
    }
    return 0;
}

树上路径

有些题目会给你一棵树，问你树上两点间路径上的第k大

怎么解决呢？

可以发现，这个东西是可以进行差分的

比如说，u到v路径上的权值和，可以变成sum[u]+sum[v]−sum[lca]−sum[lcafa]
然后套到主席树上，就是小于某个数的个数，同样也可以差分出来表示

但问题是主席树怎么建呢？

我们发现，因为要求lca，我们可以在树剖dfs的时候顺便加点

具体来说，就是用fa[i]的信息更新i点的信息

以bzoj2588 洛谷p2633. count on a tree为例

//minamoto
#include
#define N 100005
#define M 2000005
using namespace std;
inline int read(){
    #define num ch-'0'
    char ch;bool flag=0;int res;
    while(!isdigit(ch=getchar()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getchar());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
int sum[M],L[M],R[M];
int a[N],b[N],rt[N];
int fa[N],sz[N],d[N],ver[N<<1],Next[N<<1],head[N],son[N],top[N];
int n,q,m,cnt=0,tot=0,ans=0;
void update(int last,int &now,int l,int r,int x){
    sum[now=++cnt]=sum[last]+1;
    if(l==r) return;
    int mid=(l+r)>>1;
    if(x<=mid) R[now]=R[last],update(L[last],L[now],l,mid,x);
    else L[now]=L[last],update(R[last],R[now],mid+1,r,x);
}
inline void add(int u,int v){
    ver[++tot]=v,Next[tot]=head[u],head[u]=tot;
    ver[++tot]=u,Next[tot]=head[v],head[v]=tot;
}
void dfs(int u){
    sz[u]=1,d[u]=d[fa[u]]+1;
    update(rt[fa[u]],rt[u],1,m,a[u]);
    for(int i=head[u];i;i=Next[i]){
        int v=ver[i];
        if(v==fa[u]) continue;
        fa[v]=u,dfs(v);
        sz[u]+=sz[v];
        if(!son[u]||sz[v]>sz[son[u]]) son[u]=v;
    }
}
void dfs(int u,int tp){
    top[u]=tp;
    if(!son[u]) return;
    dfs(son[u],tp);
    for(int i=head[u];i;i=Next[i]){
        int v=ver[i];
        if(v==son[u]||v==fa[u]) continue;
        dfs(v,v);
    }
}
int LCA(int x,int y){
    while(top[x]!=top[y])
    d[top[x]]>=d[top[y]]?x=fa[top[x]]:y=fa[top[y]];
    return d[x]>=d[y]?y:x;
}
int query(int ql,int qr,int lca,int lca_fa,int l,int r,int k){
    if(l>=r) return l;
    int x=sum[L[ql]]+sum[L[qr]]-sum[L[lca]]-sum[L[lca_fa]];
    int mid=(l+r)>>1;
    if(x>=k) return query(L[ql],L[qr],L[lca],L[lca_fa],l,mid,k);
    else return query(R[ql],R[qr],R[lca],R[lca_fa],mid+1,r,k-x);
}
int main(){
    //freopen("testdata.in","r",stdin);
    n=read(),q=read();
    for(int i=1;i<=n;++i)
    b[i]=a[i]=read();
    sort(b+1,b+1+n);
    m=unique(b+1,b+1+n)-b-1;
    for(int i=1;i<=n;++i)
    a[i]=lower_bound(b+1,b+1+m,a[i])-b;
    for(int i=1;i<n;++i){
        int u=read(),v=read();
        add(u,v);
    }
    dfs(1),dfs(1,1);
    while(q--){
        int x,y,z,lca;
        x=read(),y=read(),z=read();
        x^=ans,lca=LCA(x,y);
        ans=b[query(rt[x],rt[y],rt[lca],rt[fa[lca]],1,m,z)];
        printf("%d\n",ans);
    }
    return 0;
}

[bzoj3123][洛谷P3302] [SDOI2013]森林

路经查询就是主席树维护，而连接两棵树就是用启发式合并

//minamoto
#include
using namespace std;
inline int read(){
    #define num ch-'0'
    char ch;bool flag=0;int res;
    while(!isdigit(ch=getchar()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getchar());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
const int N=80005,M=N*200;
int ver[N<<2],Next[N<<2],head[N];
int a[N],fa[N],sz[N],b[N];
int n,m,tot,q,size,ans;
void add(int u,int v){
    ver[++tot]=v,Next[tot]=head[u],head[u]=tot;
    ver[++tot]=u,Next[tot]=head[v],head[v]=tot;
}
int L[M],R[M],sum[M],rt[N],cnt;
void update(int last,int &now,int l,int r,int x){
    sum[now=++cnt]=sum[last]+1;
    if(l==r) return;
    int mid=(l+r)>>1;
    if(x<=mid) R[now]=R[last],update(L[last],L[now],l,mid,x);
    else L[now]=L[last],update(R[last],R[now],mid+1,r,x);
}
int query(int u,int v,int lca,int lca_fa,int l,int r,int k){
    if(l>=r) return l;
    int x=sum[L[v]]+sum[L[u]]-sum[L[lca]]-sum[L[lca_fa]];
    int mid=(l+r)>>1;
    if(x>=k) return query(L[u],L[v],L[lca],L[lca_fa],l,mid,k);
    else return query(R[u],R[v],R[lca],R[lca_fa],mid+1,r,k-x);
}
inline int hash(int x){
    return lower_bound(b+1,b+1+size,x)-b;
}
int ff(int x){
    return fa[x]==x?x:fa[x]=ff(fa[x]);
}
int st[N][17],d[N],vis[N];
void dfs(int u,int father,int root){
    st[u][0]=father;
    for(int i=1;i<=16;++i)
    st[u][i]=st[st[u][i-1]][i-1];
    ++sz[root];
    d[u]=d[father]+1;
    fa[u]=root;
    vis[u]=1;
    update(rt[father],rt[u],1,size,hash(a[u]));
    for(int i=head[u];i;i=Next[i]){
        int v=ver[i];
        if(v==father) continue;
        dfs(v,u,root);
    }
}
int LCA(int x,int y){
    if(x==y) return x;
    if(d[x]<d[y]) swap(x,y);
    for(int i=16;i>=0;--i){
        if(d[st[x][i]]>=d[y]) x=st[x][i];
    }
    if(x==y) return x;
    for(int i=16;i>=0;--i){
        if(st[x][i]!=st[y][i])
        x=st[x][i],y=st[y][i];
    }
    return st[x][0];
}
int main(){
    //freopen("testdata.in","r",stdin);
    int t=read();
    n=read(),m=read(),q=read();
    for(int i=1;i<=n;++i)
    a[i]=b[i]=read(),fa[i]=i;
    sort(b+1,b+1+n);
    size=unique(b+1,b+1+n)-b-1;
    for(int i=1;i<=m;++i){
        int u=read(),v=read();
        add(u,v);
    }
    for(int i=1;i<=n;++i)
    if(!vis[i]) dfs(i,0,i);
    while(q--){
        char ch;int x,y;
        while(!isupper(ch=getchar()));
        x=read()^ans,y=read()^ans;
        if(ch=='Q'){
            int k=read()^ans;
            int lca=LCA(x,y);
            ans=b[query(rt[x],rt[y],rt[lca],rt[st[lca][0]],1,size,k)];
            printf("%d\n",ans);
        }
        else{
            add(x,y);
            int u=ff(x),v=ff(y);
            if(sz[u]<sz[v]) swap(x,y),swap(u,v);
            dfs(y,x,u);
        }
    }
    return 0;
}

洛谷P3066 [USACO12DEC]逃跑的BarnRunning Away From…

题意

给出以1号点为根的一棵有根树,问每个点的子树中与它距离小于等于l的点有多少个

题解

似乎有好多种做法啊……然而蒟蒻只会打打主席树的板子……

调了一个上午一直WA……狠下心来重打一遍居然直接一遍过……

先dfs一遍，把到根节点的距离算出来，然后建出树上的主席树

然后考虑，d[v]−d[u]<=L，d[v]<=L+d[u]
然后就是对于每一个d[u]+L查询一下区间内有多少比它小的就好

细节问题：因为不能保证d[u]+L在离散化后的数组内存在，所以要用upper_bound，并查询比它小的，而且要在离散化的数组后面加一个inf
要对每一个子树进行操作，怎么做呢？

我们可以直接dfs这棵树，并记录下进入一个点的编号l[i]和从这个点出去时的编号r[i]
那么这个点的子树的区间一定是[l[i],r[i]]
然后直接在树上查询就行了

//minamoto
#include
#define N 200005
#define M 4000005
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
inline ll read(){
    #define num ch-'0'
    char ch;bool flag=0;ll res;
    while(!isdigit(ch=getchar()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getchar());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
int sum[M],L[M],R[M],rt[N];
int ver[N<<1],Next[N<<1],head[N];ll edge[N<<1];
int ls[N],rs[N];ll a[N],b[N];
int n,m,cnt,tot;ll p;
void update(int last,int &now,int l,int r,int x){
    sum[now=++cnt]=sum[last]+1;
    if(l==r) return;
    int mid=(l+r)>>1;
    if(x<=mid) R[now]=R[last],update(L[last],L[now],l,mid,x);
    else L[now]=L[last],update(R[last],R[now],mid+1,r,x);
}
int query(int u,int v,int l,int r,int k){
    if(r<k) return sum[v]-sum[u];
    if(l>=k) return 0;
    int mid=(l+r)>>1;
    if(k<=mid) return query(L[u],L[v],l,mid,k);
    else return query(R[u],R[v],mid+1,r,k)+sum[L[v]]-sum[L[u]];
}
inline void add(int u,int v,ll e){
    ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e;
}
void dfs(int u,int fa,ll d){
    b[ls[u]=++m]=d,a[m]=d;
    for(int i=head[u];i;i=Next[i])
    if(ver[i]!=fa) dfs(ver[i],u,d+edge[i]);
    rs[u]=m;
}
int main(){
    n=read(),p=read();
    for(int u=2;u<=n;++u){
        int v=read();ll e=read();
        add(v,u,e);
    }
    dfs(1,0,0);
    sort(b+1,b+1+m);
    m=unique(b+1,b+1+m)-b-1;
    for(int i=1;i<=n;++i){
        int k=lower_bound(b+1,b+1+m,a[i])-b;
        update(rt[i-1],rt[i],1,m,k);
    }
    b[m+1]=inf;
    for(int i=1;i<=n;++i){
        int k=upper_bound(b+1,b+2+m,a[ls[i]]+p)-b;
        k=query(rt[ls[i]-1],rt[rs[i]],1,m,k);
        printf("%d\n",k);
    }
    return 0;
}

bzoj 1803: Spoj1487 Query on a tree III(主席树)

题意

你被给定一棵带点权的n个点的有根数，点从1到n编号。

定义查询 query(x,k): 寻找以x为根的k大点的编号（从小到大排序第k个点）

假设没有两个相同的点权。

输入格式： 第一行为整数n，第二行为点权，接下来n-1行为树边，接下来一行为整数m，下面m行为两个整数x,k，代表query(x,k)

输出格式： m行，输出每次查询的结果。

题解

先一遍dfs，然后建个主席树，带上去直接跑一跑就好了

我忘了注意dfs序的位置和原来的编号……结果调了半天啥都调不出来……

//minamoto
#include
#include
#include
using namespace std;
#define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
inline int read(){
    #define num ch-'0'
    char ch;bool flag=0;int res;
    while(!isdigit(ch=getc()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getc());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
char obuf[1<<24],*o=obuf;
inline void print(int x){
    if(x>9) print(x/10);
    *o++=x%10+48;
}
const int N=100005,M=N*30;
int sum[M],L[M],R[M],rt[N];
int ver[N<<1],Next[N<<1],head[N];
int ls[N],rs[N],a[N],b[N],id[N],pos[N];
int n,m,cnt,tot,q;
void update(int last,int &now,int l,int r,int x){
    sum[now=++cnt]=sum[last]+1;
    if(l==r) return;
    int mid=(l+r)>>1;
    if(x<=mid) R[now]=R[last],update(L[last],L[now],l,mid,x);
    else L[now]=L[last],update(R[last],R[now],mid+1,r,x);
}
int query(int u,int v,int l,int r,int k){
    if(l>=r) return l;
    int x=sum[L[v]]-sum[L[u]];
    int mid=(l+r)>>1;
    if(x>=k) return query(L[u],L[v],l,mid,k);
    else return query(R[u],R[v],mid+1,r,k-x);
}
inline void add(int u,int v){
    ver[++tot]=v,Next[tot]=head[u],head[u]=tot;
    ver[++tot]=u,Next[tot]=head[v],head[v]=tot;
}
void dfs(int u,int fa){
    a[ls[u]=++m]=b[u],id[m]=u;
    for(int i=head[u];i;i=Next[i])
    if(ver[i]!=fa) dfs(ver[i],u);
    rs[u]=m;
}
int main(){
    //freopen("testdata.in","r",stdin);
    n=read();
    for(int i=1;i<=n;++i) b[i]=read();
    for(int i=1;i<n;++i){
        int u,v;
        u=read(),v=read();
        add(u,v);
    }
    dfs(1,0);
    sort(b+1,b+1+m);
    for(int i=1;i<=n;++i){
        int k=lower_bound(b+1,b+1+m,a[i])-b;
        update(rt[i-1],rt[i],1,m,k);
        pos[k]=id[i];
    }
    q=read();
    while(q--){
        int u=read(),k=read();
        int ans=pos[query(rt[ls[u]-1],rt[rs[u]],1,m,k)];
        print(ans),*o++='\n';
    }
    fwrite(obuf,o-obuf,1,stdout);
    return 0;
}

带修改主席树

我们可以发现，主席树每一棵线段树维护的都是一个前缀和

如果有修改操作，每一次都要对后面的所有的前缀和都进行修改，那样的话时间复杂度就太爆炸了

我们可以考虑一下树状数组

树状数组维护的也是前缀和，但它的每一次修改是O(logn)的

他的节点存的并不是前缀和，而是一颗线段树，但我们仍可以用树状数组来求出前缀和

于是我们可以用树状数组的思想来维护，主席树

用树状数组存一下每个节点的位置，每一次修改都按树状数组的方法去修改，也就是说并不需要修改那么多节点

查询的时候，也按树状数组的方法查询就好了

建议对这段话仔细理解，我当初也是懵逼了好久，最后看了zcysky大佬的那篇blog才蓦然醒悟的

拿bzoj1901洛谷P2617 Dynamic Rankings为例

题意：有n个数，m次操作，操作有两种:

Q l r k :查询区间[l, r]中第K大的数

C i v :将第i个数改为v

是一个带修改主席树的板子，注意离散化的时候，记得把询问的，修改的都给放到数组里，同时离散化。

思路就按我上面所说的

这道题目以及下面代码的个人总结：
动态更改，做法其实就是树状数组套主席树，树状数组的每一个点就是一颗i位置的线段树，树状数组每次更新用树状数组的形式更新某几个节点，然后每棵树递归的往下更新下面的节点。

//minamoto
#include
#define N 10005
using namespace std;
inline int read(){
    #define num ch-'0'
    char ch;bool flag=0;int res;
    while(!isdigit(ch=getchar()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getchar());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
inline int lowbit(int x){return x&(-x);}
int sum[N*600],L[N*600],R[N*600];
int xx[N],yy[N],rt[N],a[N],b[N<<1],ca[N],cb[N],cc[N];
int n,q,m,cnt=0,totx,toty;
// now开的是引用，所以他会一直变。。所以下面传入now的是rt[i],所以rt[i]就有now最浅层递归的值了，因为之后递归的是L[now],R[now]
void update(int last,int &now,int l,int r,int x,int v){ // 对树桩数组的更新来对每棵
//线段树从头更新，一共logn次更新，v代表是+-1
    sum[now=++cnt]=sum[last]+v;  //开一个新的节点
    L[now]=L[last],R[now]=R[last];  //赋值
    if(l==r) return;
    int mid=(l+r)>>1;
    if(x<=mid) update(L[last],L[now],l,mid,x,v);  
    else update(R[last],R[now],mid+1,r,x,v);
}
int query(int l,int r,int q){
    if(l==r) return l;
    int x=0,mid=(l+r)>>1;
    for(int i=1;i<=totx;++i) x-=sum[L[xx[i]]]; // 统计之前先更新，把前面的剪掉
    for(int i=1;i<=toty;++i) x+=sum[L[yy[i]]]; 
    if(q<=x){
        for(int i=1;i<=totx;++i) xx[i]=L[xx[i]]; // 递归更新节点的编号
        for(int i=1;i<=toty;++i) yy[i]=L[yy[i]];
        return query(l,mid,q);
    }
    else{
        for(int i=1;i<=totx;++i) xx[i]=R[xx[i]];
        for(int i=1;i<=toty;++i) yy[i]=R[yy[i]];
        return query(mid+1,r,q-x);
    }
}
void add(int x,int y){  //x是要修改的位置，y是 +-1
    int k=lower_bound(b+1,b+1+m,a[x])-b;  // 离散化，获取a[x]的离散值
    for(int i=x;i<=n;i+=lowbit(i)) update(rt[i],rt[i],1,m,k,y); //存的不是前缀和了，但是可以通过BIT求出前缀和
}
int main(){
    //freopen("testdata.in","r",stdin);
    n=read(),q=read();
    for(int i=1;i<=n;++i)
    b[++m]=a[i]=read();
    for(int i=1;i<=q;++i){
        char ch;
        while(!isupper(ch=getchar()));
        ca[i]=read(),cb[i]=read();  // 
        if(ch=='Q') cc[i]=read();else b[++m]=cb[i]; // cc代表k，cb带表要改的数
    }
    sort(b+1,b+1+m);
    m=unique(b+1,b+1+m)-b-1;  //去重之后的数量
    for(int i=1;i<=n;++i) add(i,1);  // 初始化每个数都+1，每个数字都遍历，所以可以同时初始化好主席树
    for(int i=1;i<=q;++i){
        if(cc[i]){  // 如果是q
            totx=toty=0;
            for(int j=ca[i]-1;j;j-=lowbit(j)) xx[++totx]=rt[j]; //l-1的BIT的线段树的根的编号
            for(int j=cb[i];j;j-=lowbit(j)) yy[++toty]=rt[j];  // r的BIT的线段树的根的编号
            printf("%d\n",b[query(1,m,cc[i])]);
        }
        else{add(ca[i],-1),a[ca[i]]=cb[i],add(ca[i],1);}  // 否则就是改动，把原来的数字删掉加上要变成的数字
    }
    return 0;
}

一个不错的题解
他是通过两棵树，一颗维护主席树，一颗维护树状数组
代码：

#include
#include
#include
#include
using namespace std;
const int maxn = 6e4+5; //n+m
int a[maxn], Hash[maxn];
int T[maxn], lson[maxn<<5], rson[maxn<<5], sum[maxn<<5];
int S[maxn];
int n, m, tot;
struct node
{
    int l, r, k;
    bool Q;  // q判断是否是询问的
}op[maxn];
 
int build(int l, int r)  // 建树
{
    int rt = tot++;
    sum[rt] = 0;
    if(l != r)
    {
        int mid = (l+r)/2;
        lson[rt] = build(l, mid);
        rson[rt] = build(mid+1, r);
    }
    return rt;
}
 
int update(int pre, int l, int r, int x, int val)
{
    int rt = ++tot;
    lson[rt] = lson[pre], rson[rt] = rson[pre], sum[rt] = sum[pre]+val;
    if(l < r)
    {
        int mid = (l+r)/2;
        if(x <= mid)
            lson[rt] = update(lson[pre], l, mid, x, val);
        else
            rson[rt] = update(rson[pre], mid+1, r, x, val);
    }
    return rt;
}
 
int lowbit(int x)
{
    return x&(-x);
}
 
int use[maxn];  // use记录通过树状数组的格式更新哪几棵树
 
int Sum(int x)
{
    int res = 0;
    while(x)
    {
        res += sum[lson[use[x]]];
        x -= lowbit(x);
    }
    return res;
}
 
int query(int u, int v, int lr, int rr, int l, int r, int k)
{
    if(l >= r) return l;
    int mid = (l+r)/2;
    int tmp = Sum(v)-Sum(u)+sum[lson[rr]]-sum[lson[lr]];
    if(tmp >= k)
    {
        for(int i = u; i; i -= lowbit(i))
            use[i] = lson[use[i]];
        for(int i = v; i; i -= lowbit(i))
            use[i] = lson[use[i]];
        return query(u, v, lson[lr], lson[rr], l, mid, k);
    }
    else
    {
        for(int i = u; i; i -= lowbit(i))
            use[i] = rson[use[i]];
        for(int i = v; i; i -= lowbit(i))
            use[i] = rson[use[i]];
        return query(u, v, rson[lr], rson[rr], mid+1, r, k-tmp);
    }
}
 
void modify(int x, int p, int d)
{
    while(x <= n)
    {
        S[x] = update(S[x], 1, m, p, d);
        x += lowbit(x);
    }
}
 
int main(void)
{
    int t;
    cin >> t;
    while(t--)
    {
        int q;
        scanf("%d%d", &n, &q);
        tot = m = 0;
        for(int i = 1; i <= n; i++)
        {
            scanf("%d", &a[i]);
            Hash[++m] = a[i];
        }
        for(int i = 0; i < q; i++)
        {
            char cmd[10];
            scanf(" %s", cmd);
            if(cmd[0] == 'Q')
            {
                scanf("%d%d%d", &op[i].l, &op[i].r, &op[i].k);
                op[i].Q = 1;
            }
            else
            {
                scanf("%d%d", &op[i].l, &op[i].r);
                op[i].Q = 0;
                Hash[++m] = op[i].r;
            }
        }
        sort(Hash+1, Hash+1+m);
        int mm = unique(Hash+1, Hash+1+m)-Hash-1;
        m = mm;
        T[0] = build(1, m);
        for(int i = 1; i <= n; i++)
            T[i] = update(T[i-1], 1, m, lower_bound(Hash+1, Hash+1+m, a[i])-Hash, 1);
        for(int i = 1; i <= n; i++)
            S[i] = T[0];
        for(int i = 0; i < q; i++)
        {
            if(op[i].Q)
            {
                for(int j = op[i].l-1; j; j-=lowbit(j))
                    use[j] = S[j];
                for(int j = op[i].r; j; j-=lowbit(j))
                    use[j] = S[j];
                printf("%d\n", Hash[query(op[i].l-1, op[i].r, T[op[i].l-1], T[op[i].r], 1, m, op[i].k)]);
            }
            else
            {
                modify(op[i].l, lower_bound(Hash+1, Hash+1+m, a[op[i].l])-Hash, -1);
                modify(op[i].l, lower_bound(Hash+1, Hash+1+m, op[i].r)-Hash, 1);
                a[op[i].l] = op[i].r;
            }
        }
    }
    return 0;
}

还有一道[BZOJ3295] [Cqoi2011]洛谷p3157动态逆序对
题解

//minamoto
#include
#define N 100005
#define M 5000005
#define ll long long
using namespace std;
inline ll read(){
    #define num ch-'0'
    char ch;bool flag=0;ll res;
    while(!isdigit(ch=getchar()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getchar());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
int L[M],R[M],sum[M],rt[N];
int val[N],pos[N],xx[N],yy[N],c[N],a1[N],a2[N];
int n,cnt,q;ll ans=0;
inline int lowbit(int x){return x&(-x);}
int ask(int x){
    int s=0;
    for(int i=x;i;i-=lowbit(i)) s+=c[i];
    return s;
}
void update(int &now,int l,int r,int k){
    if(!now) now=++cnt;
    ++sum[now];
    if(l==r) return;
    int mid=(l+r)>>1;
    if(k<=mid) update(L[now],l,mid,k);
    else update(R[now],mid+1,r,k);
}
int querysub(int x,int y,int v){
    int cntx=0,cnty=0,ans=0;--x;
    for(int i=x;i;i-=lowbit(i)) xx[++cntx]=rt[i];
    for(int i=y;i;i-=lowbit(i)) yy[++cnty]=rt[i];
    int l=1,r=n;
    while(l<r){
        int mid=(l+r)>>1;
        if(v<=mid){
            for(int i=1;i<=cntx;++i) ans-=sum[R[xx[i]]];
            for(int i=1;i<=cnty;++i) ans+=sum[R[yy[i]]];
            for(int i=1;i<=cntx;++i) xx[i]=L[xx[i]];
            for(int i=1;i<=cnty;++i) yy[i]=L[yy[i]];
            r=mid;
        }
        else{
            for(int i=1;i<=cntx;++i) xx[i]=R[xx[i]];
            for(int i=1;i<=cnty;++i) yy[i]=R[yy[i]];
            l=mid+1;
        }
    }
    return ans;
}
int querypre(int x,int y,int v){
    int cntx=0,cnty=0,ans=0;--x;
    for(int i=x;i;i-=lowbit(i)) xx[++cntx]=rt[i];
    for(int i=y;i;i-=lowbit(i)) yy[++cnty]=rt[i];
    int l=1,r=n;
    while(l<r){
        int mid=(l+r)>>1;
        if(v>mid){
            for(int i=1;i<=cntx;++i) ans-=sum[L[xx[i]]];
            for(int i=1;i<=cnty;++i) ans+=sum[L[yy[i]]];
            for(int i=1;i<=cntx;++i) xx[i]=R[xx[i]];
            for(int i=1;i<=cnty;++i) yy[i]=R[yy[i]];
            l=mid+1;
        }
        else{
            for(int i=1;i<=cntx;++i) xx[i]=L[xx[i]];
            for(int i=1;i<=cnty;++i) yy[i]=L[yy[i]];
            r=mid;
        }
    }
    return ans;
}
int main(){
    //freopen("testdata.in","r",stdin);
    n=read(),q=read();
    for(int i=1;i<=n;++i){
        val[i]=read(),pos[val[i]]=i;
        a1[i]=ask(n)-ask(val[i]);
        ans+=a1[i];
        for(int j=val[i];j<=n;j+=lowbit(j)) ++c[j];
    }
    memset(c,0,sizeof(c));
    for(int i=n;i;--i){
        a2[i]=ask(val[i]-1);
        for(int j=val[i];j<=n;j+=lowbit(j)) ++c[j];
    }
    while(q--){
        printf("%lld\n",ans);
        int x=read();x=pos[x];
        ans-=(a1[x]+a2[x]-querysub(1,x-1,val[x])-querypre(x+1,n,val[x]));
        for(int j=x;j<=n;j+=lowbit(j)) update(rt[j],1,n,val[x]);
    }
    return 0;
}

进阶

【bzoj2653】【middle】【主席树+二分答案】

Description
一个长度为 n 的序列 a ，设其排过序之后为 b ，其中位数定义为 b[n/2] ，其中 a,b 从 0 开始标号 , 除法取下整。
给你一个长度为 n 的序列 s 。回答 Q 个这样的询问 ： s 的左端点在 [a,b] 之间 , 右端点在 [c,d] 之间的子序列中 ，最大的中位数。
其中 a

Solution
对着题解理解了半天……又对着代码调了半天……最后发现竟然是一个函数名没写orz

不过不得不说这题真的是主席树好题

先考虑二分答案，找出区间内比mid小的数有多少

因为对答案的贡献只有有或没有，所以可以把比mid小的都设为-1，比mid大的都设为1，如果区间内的和大于等于0，说明mid可行，继续二分下去

然而如果离散之后对每一个值建树，空间毫无疑问爆炸

于是只要用主席树维护一下就可以了

//minamoto
#include
#include
#include
using namespace std;
#define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
inline int read(){
    #define num ch-'0'
    char ch;bool flag=0;int res;
    while(!isdigit(ch=getc()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getc());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
char obuf[1<<24],*o=obuf;
inline void print(int x){
    if(x>9) print(x/10);
    *o++=x%10+48;
}
const int N=20005,M=N*30;
int n,Pre,q,cnt;
int rt[N],p[5];
struct node{
    int l,r,lmx,rmx,sum;
}t[M],op;
struct data{
    int x,id;
    inline bool operator <(const data &b)const
    {return x<b.x;}
}a[N];
inline void pushup(int x){
    t[x].sum=t[t[x].l].sum+t[t[x].r].sum;
    t[x].lmx=max(t[t[x].l].lmx,t[t[x].l].sum+t[t[x].r].lmx);
    t[x].rmx=max(t[t[x].r].rmx,t[t[x].r].sum+t[t[x].l].rmx);
}
void build(int &now,int l,int r){
    now=++cnt;
    if(l==r){t[now].lmx=t[now].rmx=t[now].sum=1;return;}
    int mid=(l+r)>>1;
    build(t[now].l,l,mid);
    build(t[now].r,mid+1,r);
    pushup(now);
}
void update(int last,int &now,int l,int r,int k){
    now=++cnt;
    if(l==r){t[now].lmx=t[now].rmx=t[now].sum=-1;return;}
    int mid=(l+r)>>1;
    if(k<=mid) t[now].r=t[last].r,update(t[last].l,t[now].l,l,mid,k);
    else t[now].l=t[last].l,update(t[last].r,t[now].r,mid+1,r,k);
    pushup(now);
}
node merge(node x,node y){
    node z;
    z.sum=x.sum+y.sum;
    z.lmx=max(x.lmx,x.sum+y.lmx);
    z.rmx=max(y.rmx,y.sum+x.rmx);
    return z;
}
node find(int x,int l,int r,int y,int z){
    if(y>z) return op;
    if(l==y&&r==z) return t[x];
    int mid=(l+r)>>1;
    if(z<=mid) return find(t[x].l,l,mid,y,z);
    else if(y>mid) return find(t[x].r,mid+1,r,y,z);
    else return merge(find(t[x].l,l,mid,y,mid),find(t[x].r,mid+1,r,mid+1,z));
}
int query(int x){
    return find(rt[x],1,n,p[1],p[2]).rmx+find(rt[x],1,n,p[2]+1,p[3]-1).sum+find(rt[x],1,n,p[3],p[4]).lmx;
}
int main(){
    //freopen("testdata.in","r",stdin);
    n=read();
    for(int i=1;i<=n;++i) a[i].x=read(),a[i].id=i;
    sort(a+1,a+1+n);
    build(rt[1],1,n);
    for(int i=2;i<=n;++i) update(rt[i-1],rt[i],1,n,a[i-1].id);
    q=read();
    while(q--){
        int x=read(),y=read(),z=read(),k=read();
        p[1]=(x+Pre)%n+1,p[2]=(y+Pre)%n+1,p[3]=(z+Pre)%n+1,p[4]=(k+Pre)%n+1;
        sort(p+1,p+5);
        int l=1,r=n,ans=1;
        while(l<=r){
            int mid=(l+r)>>1;
            int f=query(mid);
            if(f>=0) ans=mid,l=mid+1;
            else r=mid-1;
        }
        Pre=a[ans].x;
        print(a[ans].x),*o++='\n';
    }
    fwrite(obuf,o-obuf,1,stdout);
    return 0;
}

hdu 4348 To the moon 主席树的区间修改

题意：

一个长度为n的数组，4种操作 ：

（1）C l r d：区间[l,r]中的数都加1，同时当前的时间戳加1 。

（2）Q l r：查询当前时间戳区间[l,r]中所有数的和 。

（3）H l r t：查询时间戳t区间[l,r]的和 。

（4）B t：将当前时间戳置为t 。

所有操作均合法 。

题解

原来……主席树真的能做可持久化的啊……花了一个下午才搞明白……（虽然是看题解的）

先考虑一下，如果直接每一次修改的话，一共要修改r−l+1次，空间复杂度绝对爆炸

然后考虑一下线段树的打懒标记，可不可以套到主席树上来？

我们发现可以这么做，于是每一次修改区间时，如果区间相等，直接打上标记，等到查询的时候，再把标记给加上去

ps：更改时间的时候可以直接把cnt改成rt[t+1]−1，这样的话可以回收空间

//minamoto
#include
#define ll long long
using namespace std;
const int N=100005,M=N*30;
int n,m,cnt,rt[N];
int L[M],R[M];ll sum[M],add[M];
#define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
inline ll read(){
    #define num ch-'0'
    char ch;bool flag=0;ll res;
    while(!isdigit(ch=getc()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getc());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
void build(int &now,int l,int r){
    add[now=++cnt]=0;
    if(l==r) return (void)(sum[now]=read());
    int mid=(l+r)>>1;
    build(L[now],l,mid);
    build(R[now],mid+1,r);
    sum[now]=sum[L[now]]+sum[R[now]];
}
void update(int last,int &now,int l,int r,int ql,int qr,int x){
    now=++cnt;
    L[now]=L[last],R[now]=R[last],add[now]=add[last],sum[now]=sum[last];
    sum[now]+=1ll*x*(qr-ql+1);
    if(ql==l&&qr==r) return (void)(add[now]+=x);
    int mid=(l+r)>>1;
    if(qr<=mid) update(L[last],L[now],l,mid,ql,qr,x);
    else if(ql>mid) update(R[last],R[now],mid+1,r,ql,qr,x);
    else return (void)(update(L[last],L[now],l,mid,ql,mid,x),update(R[last],R[now],mid+1,r,mid+1,qr,x));
}
ll query(int now,int l,int r,int ql,int qr){
    if(l==ql&&r==qr) return sum[now];
    int mid=(l+r)>>1;
    ll res=1ll*add[now]*(qr-ql+1);
    if(qr<=mid) res+=query(L[now],l,mid,ql,qr);
    else if(ql>mid) res+=query(R[now],mid+1,r,ql,qr);
    else res+=query(L[now],l,mid,ql,mid)+query(R[now],mid+1,r,mid+1,qr);
    return res;
}
int main(){
    //freopen("testdata.in","r",stdin);
    n=read(),m=read();
    cnt=-1;
    build(rt[0],1,n);
    int now=0;
    while(m--){
        char ch;int l,r,x;
        while(!isupper(ch=getc()));
        switch(ch){
            case 'C':{
                l=read(),r=read(),x=read();
                ++now;
                update(rt[now-1],rt[now],1,n,l,r,x);
                break;
            }
            case 'Q':{
                l=read(),r=read();
                printf("%lld\n",query(rt[now],1,n,l,r));
                break;
            }
            case 'H':{
                l=read(),r=read(),x=read();
                printf("%lld\n",query(rt[x],1,n,l,r));
                break;
            }
            case 'B':{
                now=read();
                cnt=rt[now+1]-1;
                break;
            }
        }
    }
    return 0;
}