前缀树的数据结构以及O(n)解决子数组最大异或和的问题
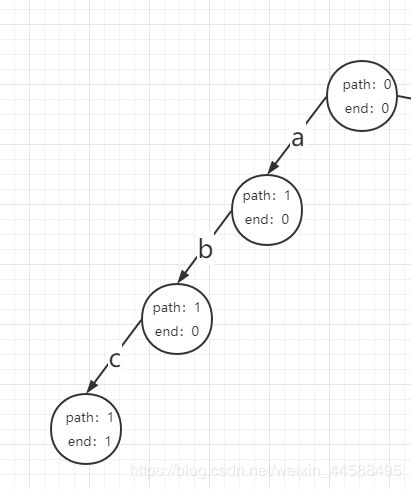
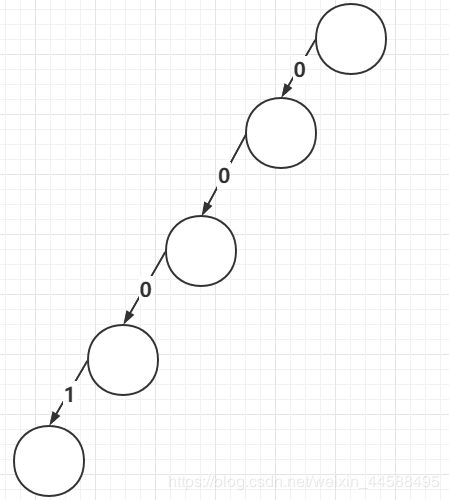
什么是前缀树,比如你输入了一个字符串“abc”:那么前缀树如图所示:
依次在头节点下创建节点,然后线上是字母(并非节点是)
每个节点上面有两个值:path(代表有多少字符串经过了该节点)、end(有多少字符串以该节点结尾)。
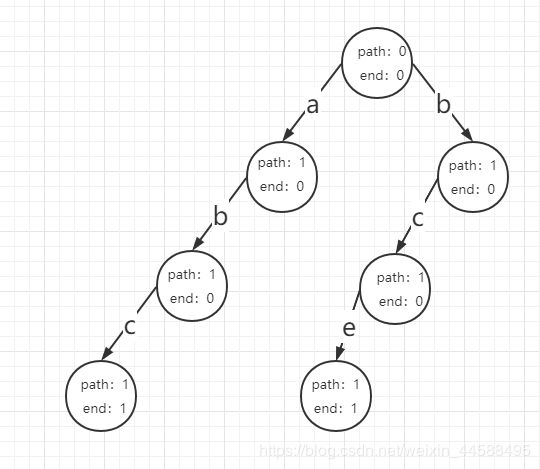
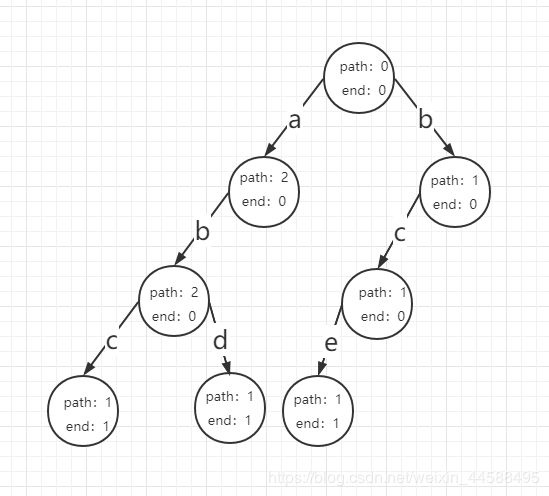
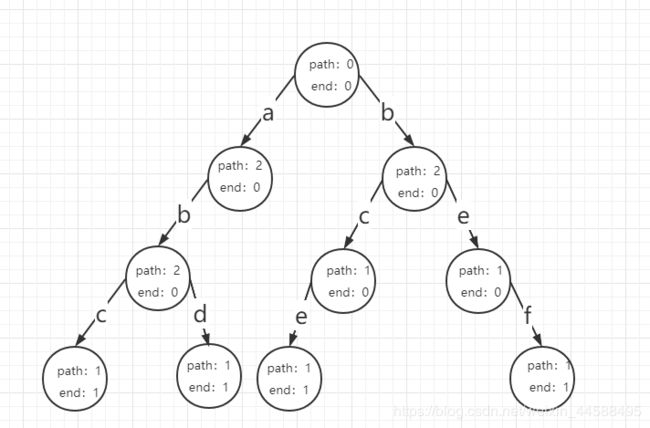
现在依次输入:“abc”、“bce”、“abd”、“bef”
输入第二个字符串:
输入第三个字符串:实际上输入abd的时候,之前已经输入abc了,可以复用之前的前缀ab。更新path。
输入第四个字符串,符用b前缀:
我们的头节点其实是没用的,字符串的下方节点才是有用的。
我们来看下面的代码:
这个就是节点类型,一起前缀的构造方法就是建造一个root,表明根节点,这里的nexts就是下层节点的指针,我们假设这个字符串中只有二十六个字母,所以数组长度是26,也就是下面的节点有26个可能,当然你也可以用map结构来做。这样可以任意字符
public class Trip {
public static class TripNode{
//讲过此节点的字符串的数量
public int path;
//以节点结尾的字符串的个数
public int end;
public TripNode[] nexts;
public TripNode(){
this.path = 0;
this.end = 0;
nexts = new TripNode[26];
}
}
private TripNode root;
public Trip(){
root = new TripNode();
}插入方法:
首先从字符串转换成字符,然后从根节点开始找next是否存在,利用下标是chars[i] - 'a',如果有就直接走进入这个节点,如果没有就创建这个节点。每经过一个节点path++,到达最后的时候end++
/**
* 插入
*/
public void insert(String word){
if(word == null){
return ;
}
char[] chars = word.toCharArray();
TripNode node = root;
int index = 0;
for(int i = 0;i < chars.length;i++){
index = chars[i] - 'a';
if(node.nexts[index] == null){
node.nexts[index] = new TripNode();
}
node = node.nexts[index];
node.path++;
}
node.end++;
}
查找方法:
跟插入是一样的,查找的过程中,如果发现为遍历完,但是有一个节点是null,那么直接返回,不存在这个字符串。否则返回end
/**
* 查找
*/
public int search(String word){
if(word == null){
return 0;
}
char[] chars = word.toCharArray();
TripNode node = root;
int index = 0;
for(int i = 0;i < chars.length;i++){
index = chars[i] - 'a';
if(node.nexts[index] == null){
return 0;
}
node = node.nexts[index];
}
return node.end;
}删除方法:
实际上就是先查找这个字符串有没有,如果有,对于path > 1的节点执行path--,当发现一个节点path=1的时候,说明这个节点一下是下面字符串的一个部分,直接让这个节点指向null,直接返回就可以了。
/**
* 删除
*/
public void delete(String word){
if(search(word) != 0){
char[] chars = word.toCharArray();
TripNode node = root;
int index = 0;
for(int i = 0;i < chars.length;i++){
index = chars[i] - 'a';
if(--node.nexts[index].path == 0){
node.nexts[index] = null;
return ;
}
node = node.nexts[index];
}
node.end--;
}
}就是输入一个pre的前缀字符串,然后返回这个字符串前缀的path。就是作为了多少个字符串的前缀。
/**
* 查询前缀有多少个
*/
public int prefixNumber(String pre){
if(pre == null){
return 0;
}
char[] chars = pre.toCharArray();
TripNode node = root;
int index= 0;
for(int i = 0;i < chars.length;i++){
index = chars[i] - 'a';
if(node.nexts[index] == null){
return 0;
}
node = node.nexts[index];
}
return node.path;
} /**
* O(n3)
*/
public static int getMaxEor1(int[] arr) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j <= i; j++) {
int res = 0;
//计算异或和
for (int start = j; start <= i; start++) {
res ^= arr[start];
}
max = Math.max(max, res);
}
}
return max;
}优化:时间复杂度O(n2),这里每次都保存0 - i子数组的异或和,然后放到dp里面,之后枚举子数组,然后根据dp算出异或和,然后选出最大值,这里的优化主要在于不用每一次重复计算之前的异或和。
/**
* O(n2)
*/
public static int getMaxEor2(int[] arr) {
int max = Integer.MIN_VALUE;
int[] dp = new int[arr.length];
int eor = 0;
for (int i = 0; i < arr.length; i++) {
//0 - i 的异或和
eor ^= arr[i];
max = Math.max(max, eor);
for (int start = 1; start <= i; start++) {
//计算异或和
int res = eor ^ dp[start - 1];
max = Math.max(max, res);
}
dp[i] = eor;
}
return max;
}最优解:就是前缀树,时间复杂度O(n)。这里定义一个前缀树的黑盒,你只需要了解,这个东西能够给你0 - i的最大子数组的最大异或和,至于为什么能给?之后在分析黑盒的内容。
public static int maxXorSubarray(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
int max = Integer.MIN_VALUE;
int eor = 0;
NumTrie numTrie = new NumTrie();
numTrie.add(0);
for (int i = 0; i < arr.length; i++) {
eor ^= arr[i];
//比较大小。
max = Math.max(max, numTrie.maxXor(eor));
numTrie.add(eor);
}
return max;
}eor还是0 - i的数组的异或和,numTrie就是一个黑盒,numTrie.maxXor(eor)方法就能够给你返回0 - i的最优值,然后将每一个eor放入到黑盒中。我们看图分析黑盒:
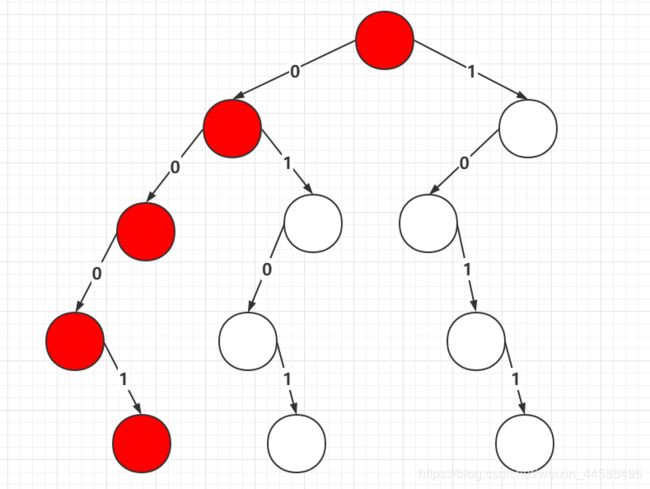
如果黑盒里面有:0 -0 、0 - 1、0 - 2、0 - 3.......、0 - i - 1的异或和,那么当计算 0 - i的最优值的时候怎么做呢?他通过黑盒选举出一个最优的值,比如选举0 - 3,那么就是 0 - 3的异或和 和 0 - i的异或和 做异或最大,那么实际上就是子数组 4 -i 的异或和最大。因为 0 - i ^ 0 - 3 实际上就等于 4 - i的异或和。
看图分析如果建立前缀树,这里运用了位运算,一个int类型32位(我们以4位为例),最高位为符号位(1代表符数,0代表正数)。
现有如下值: 0 - 0 : 0001,0 - 1:0101,0 - 2:1011。要拿取这个最大异或和0 - 3 : 0101。
首先输入0001,建立前缀树:
public static class Node {
public Node[] nexts = new Node[2];
}
public static class NumTrie {
public Node head = new Node();
public void add(int num) {
Node cur = head;
for (int move = 31; move >= 0; move--) {
int path = ((num >> move) & 1);
cur.nexts[path] = cur.nexts[path] == null ? new Node() : cur.nexts[path];
cur = cur.nexts[path];
}
}
public int maxXor(int num) {
Node cur = head;
int res = 0;
for (int move = 31; move >= 0; move--) {
int path = (num >> move) & 1;
int best = move == 31 ? path : (path ^ 1);//期待选择的路
best = cur.nexts[best] != null ? best : (best ^ 1);//实际选择的路
res |= (path ^ best) << move;//设置答案的一位
cur = cur.nexts[best];//继续向下走
}
return res;
}
}这个是前缀树的结构。add方法很简单,就是依次取出32位int整数的位值(0或者1),然后创建一个前缀树。
maxXor方法,就有点道行了,如何选取这个期待的呢?
(1)首先还是取出当前传入的节点num的高位,第一位是符号位, int path = (num >> move) & 1; path就能通过&1能够获取下走的路径,如果(num >> move)是1,那么下次走的路就是1,如果是0,那么走的路就是0。因为1 ^ 1是0,0 ^ 0是0。
(2)然后int best = move == 31 ? path : (path ^ 1);如果是符号位那么直接就是期待我要走path,如果不是符号位,我就想走,我相反的,因为相反才能保证异或是1,所以这个是期待路径。
(3)下一步就是即使你有期待的路径,但是未必前缀树中就有啊,所以呢下一个是实际的选择路径,best = cur.nexts[best] != null ? best : (best ^ 1);这个先判断期待路径是不是null,如果是null,那么走相反的路径(一个前缀树一定是有32高的一个层数的,因为我们起初add(0),所以保证了一定有0这个子树)。如果不是null,就说明有,所以直接走。
(4)res |= (path ^ best) << move;这个是设置答案,如果path(num的位值)与实际值做异或得出最优值,然后右移动放到对应的位数上,用或操作来弄。
(5)之后就是往下走!
这样就能够拿到0 - i的一个最优值。然后依次拿到 0 - i ,i = 1、2、3、......、n。的最优值,最后比较大小,取最大。