二维线图元的生成

1. 图元

• 图形描述：复杂图形既可以看作是若干点组成，也可以看作是由线段等基本几何机构组成。
• 图元：包含坐标和其它属性信息的基本几何结构称为图元，即最基本的图形元素。
• 图元的生成，是从图元的参数表示形式（由图形软件包的使用者指定）到点阵表示形式（光栅显示系统刷新时所需的表示形式）的转换。这个过程也成为扫描转换，主要工作包括确定像素集合及其颜色，显示图形对象。

2. 图形的扫描转换

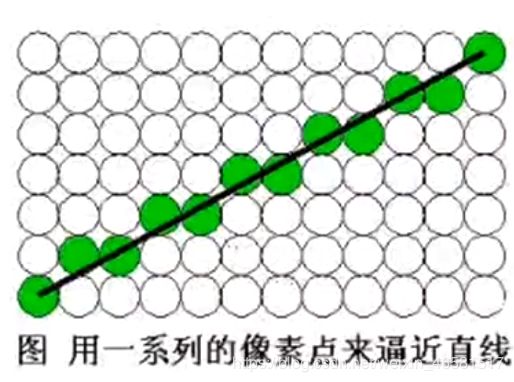
光栅图形显示器可以看作一个像素的矩阵，在光栅图形显示器上显示任何一种图像，实际上都是一些具有一种或多种颜色的像素集合，确定最佳逼近图像的像素集合，并用指定的属性写像素的过程称为图像的扫描转换或光栅化。确定一个像素集合，用于显示一个图形的过程。

• 裁剪：确定一个图形的哪些部分在窗口内，哪些部分在窗口外。

3. 直线段的扫描转换算法

确定最佳逼近于该直线的一组像素，且按扫描线顺序，对这些像素进行操作。

• 光栅扫描显示器的本质决定了它难以生成完美的直线段，也不能保证直线段精确地通过起点和重点。

直线的绘制要求：

• 直线要直：要求具有精确的起点和终点。
• 直线无方向性：从起点绘制到终点的直线段与从终点绘制到起点的直线段要重合。
• 直线的亮度、色泽要均匀。
• 画线的速度要快：即尽量使用加减法整数运算，避免乘、除、开方、三角等复杂运算，但随着计算机处理浮点数与整数的速度趋于一致，这点要求在减弱。

解决的问题：给定直线的两个端点，画出该直线。

3.1 直接求交法

假定直线的起点、终点分别为：$P_0(x_0,y_0)，P_1(x_1,y_1)$，且都为整数。则直线的参数方程为：
$$y=kx+b$$
$$k=\frac{y_1-y_0}{x_1-x_0}，b=\frac{x_1{y}_0-x_0{y}_1}{x_1-x_0}$$

• 以1个像素为单位分割区间$[x_0,x_1]$，得到$\{x_i{\}}_{i=0}^n$
• 利用直线方程计算$\{y_i\}$
• 对$y_i$取整，得到像素集$\{x_i,y_{i,r}\}$

特点

• 直观，但算法复杂度高，计算速度满，因为每一步需要一次浮点乘法、浮点加法和一次取整运算。
• 容易造成隔行显示。
  

3.2 DDA算法

• 增量算法：在一个迭代算法中，如果每一步的$x,y$值是用前一步的加上一个增量来获得，则称为增量算法。
• DDA（Digital DIfferential Analyzer, 数值微分法）算法就是一个增量算法。

特点：

• 当$x$每递增1,$y$递增$k$（即直线斜率）。
• $y_{i-1}$由$y_i$得到，不需要通过直线方程进行计算，避免了浮点乘法运算。
• $|k|>1$时，仍然避免不了隔行现实的问题。
• $y、k$必须是浮点数，且每一步都必须对$y$进行舍入取整，不利于硬件实现。

避免隔行显示：
$$\begin{gathered} y_i=k{x}_i+b \\ {y}_{i+1}=k{x}_{i+1}+b \\ =k(x_i+1)+b \\ =k{x}_i+k+b \\ =k{x}_i+b+k \end{gathered}$$

void DDALine(int x_0, int y_0, int x_1, int y_1, int color) {
	int x;
	float dx, dy, y, k;
	dx = x_1 - x_0, dy = y_1 - y_0;
	k = dy / dx, y = y_0;
	for (x = x_0; x <= x_1; x++) {
		drawpixel(x, int(y + 0.5), color);
		y = y + k;
	}
}

3.3 中点算法

假定直线斜率$0<k<1$，且已确定点亮像素点$P(x_p,y_p)$，则下一个与直线最接近的像素只能是$P_1(x_p+1,y_p)$点或$P_2(x_p+1,y_p+1)$点。设$M$为$P_1{P}_2$的中点，$Q$为$P_1{P}_2$与直线的交点。

• 直线方程：$Ax+By+C=0$，令$d=A(x_i+1)+B(y_i+0.5)+C$
• $d>0$，$M$在$Q$的上方——>$P_1$离直线更近——>取$P_1$。
• $d<0$，$M$在$Q$的下方——>$P_2$离直线更近——>取$P_2$。
• $M$与$Q$重合，$P_1$、$P_2$任取一点。

表达式：
$$y=\{\begin{array}{l}y+1(d<0)\\ y(d\ge 0)\end{array}$$
$$\begin{gathered} d_i=A(x_i+1)+B(y_i+0.5)+C \\ A=y_0-y_1 \\ B=x_1-x_0 \\ C=x_0{y}_1-x_1{y}_0 \end{gathered}$$
能否采用增量计算，提高运算效率？
$$d_{i+1}=d_i+?$$
$d$是$x,y$的线性函数，采用增量计算是可行的。

$d$值的递推公式

$$\begin{gathered} d_0=F(x_{m0},y_{m0}) \\ =F(x_i+1,y_i+0.5) \\ =A(x_i+1)+B(y_i+0.5)+C \end{gathered}$$
$d<0$
$$\begin{gathered} d_1=F(x_{m1},y_{m1}) \\ =F(x_i+2,y_i+1.5) \\ =A(x_i+1)+B(y_i+0.5)+C+A+B \\ =d_0+A+B \end{gathered}$$
$d\ge 0$
$$\begin{gathered} d_1=F(x_{m1},y_{m1}) \\ =F(x_i+2,y_i+0.5) \\ =A(x_i+1)+B(y_i+0.5)+C+A \\ =d_0+A \end{gathered}$$
计算$d$的初始值$d_0$，直线的第一个像素$P_0(x_0,y_0)$在直线上，因此相应的$d$的初始值计算如下：
$$\begin{gathered} d_0=F(x_0+1,y_0+0.5) \\ =A(x_0+1)+B(y_0+0.5)+C \\ =A{x}_0+B{y}_0+C+A+0.5B \\ =A+0.5B \end{gathered}$$
$$d_{new}=\{\begin{array}{l}{d}_{old}+A+Bd<0\\ d_{old}+Ad\ge 0\end{array}{d}_0=A+0.5B$$
特点：

• $Ax+By+C=0$，使用一般式方程
• 通过判中点的符号，最终可以只进行整数加法

void Midpoint_Line(int x_0, int y_0, int x_1, int y_1, int color) {
	int a, b, d_1, d_2, d, x, y;
	a = y_0 - y_1, b = x_1 - x_0, d = 2 * a + b;
	d_1 = 2 * a, d_2 = 2 * (a + b);
	x = x_0, y = y_0;
	drawpixel(x, y, color);
	while (x < x_1) {
		if (d < 0) {
			x++;
			y++;
			d += d_2;
		}
		else {
			x++; 
			d += d_1;
		}
		drawpixel(x, y, color);
	}
}

3.4 Bresenham

基本思想

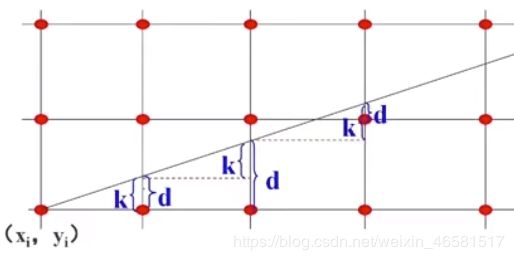
  通过各行、各列像素中心构造一组虚拟网络线，按照直线起点到终点的顺序，计算直线与各垂直网格线的交点，然后根据误差项的符号确定该列像素中与此交点最近的像素。
  假设每次$x+1,y$的递增（减）量为0或1,它取决于实际直线与最近光栅网格点的距离，这个距离的最大误差为0.5。误差项d的初值$d_0=0$
$$d=d+k$$
一旦$d\ge 1$，就把它减去1，保证d的相对性，且在0、1之间。
$$\{\begin{array}{l}{x}_{i+1}=x_i+1\\ y_{i+1}=\{\begin{array}{l}{y}_i+1(d>0.5)\\ y_i(d\le 0.5)\end{array}\end{array}$$
如何把这个算法的效率也提高到整数加法？

改进1

令$e=d-0.5$
$$\{\begin{array}{l}{x}_{i+1}=x_i+1\\ y_{i+1}=\{\begin{array}{l}{y}_i+1(e>0)\\ y_i(e\le 0)\end{array}\end{array}$$

$e=0$时，可任取上、下光栅点显示

• $e_{初}=-0.5$
• 每走一步有$e=e+k$
• if (e > 0) then e = e - 1

$k=\frac{dy}{dx}$

改进2

由于算法中只用到误差项的符号，于是可以用$e\times 2\times \Delta x$来替换$e$

• $e_{初}=-\Delta x$
• 每走一步有：$e=e+2\Delta y$
• if (e > 0) then e = e - 2$\Delta$x

算法步骤：

1. 输入直线的两端点$P_0(x_0,y_0)$和$P_1(x_1,y_1)$
2. 计算初始值$\Delta x、\Delta y、e=-\Delta x、x=x_0、y=y_0$
3. 绘制点$(x,y)$
4. $e$更新为$e+2\Delta y$，判断$e$的符号。若$e>0$，则$(x,y)$更新为$(x+1,y+1)$，同时将$e$更新为$e-2\Delta x$；否则$(x,y)$更新为$(x+1,y)$
5. 当直线没有画完时，重复步骤3和4。否则结束。