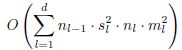深度学习研究理解9：Convolutional Neural Networks at Constrained Time Cost

本文是MSRA的何恺明在14年写的论文，通过一系列的替换实验，探讨了在限定复杂度和时间上，如何设计卷积网络结构，使得网络的性能最好。本文提出的CNN结构，在单个GPU上训练3到4天，在简单的10-view测试下获得了top-5 11.8%的准确率；做到了不仅快而且准确。

摘要：本文主要结论，1在提升准确度上深度比宽度和filter尺寸更重要；2，尽管深度很重要，如果深度随意增加分类结果会停滞，甚至降低。

一，介绍

最近提出的CNN虽然性能比Alex-net好，但是基本上都比Alex-net复杂，在训练和测试上很耗时。这些网络基本上修改了以下一些地方：1，增加宽度（filter的数量），例如zf-big模型，OverFeat-accurate模型；2，增加深度，OverFeat-accurate，VGG；3，小的间隔，ZF-net，OverFeat，VGG；或者是3者的组合使用。

这些复杂的网络不适合工业和商业的使用，此外在训练时间上也非常耗时；多以本文主要在限定时间内探究如何平衡CNN网络中深度，filter个数，间隔等影响网络复杂度的因素。

本文的核心设计是层替换（layer-replacement），通过在固定复杂度下替换实验，不仅得到了好的分类网络，而且还有助于理解卷积网络，帮助设计更好的网络。

二，相关工作

最近一些学者研究加速训练好的CNN运算速度；在一定的准确率损失下，通过近似和简化CNN网络，加速CNN计算。这些方法加速能力有限，人们更愿意找到满足限定时间要求的网络，这样不仅测试计算快速，而且还可以节省训练时间。

最近GoogLeNet提出了，inception-layer，inception是一个多路的设计，其融合了各种filter大小的特征；这个模型的理论复杂度比Alex-net复杂50%。

三，性质

3.1 基本模型

本文基于流行的三段式设计，两个pooling之间为一个阶段，提出了一个更加“苗条”的CNN网络。

具体配置如下：

Input（224,224,3）→64F(7,7,3,s=2) →max-p(3,3,3)→128F(5,5,64) →max-p(2,2,2) →256F(3,3,128) →256F(3,3,256) →256F(3,3,256) →spp(6*6,3*3,2*2,1*1) →4096fc→4096fc→softmax

和Alex-net比较改进：

1，第一层从96个filter变成64个，filter从11*11，间隔=4变成7*7 间隔=2

2，不使用overlap pooling，第一个pooling层窗口不变，间隔变为3；第二个pooling从3*3间隔=3变成2*2的窗口间隔=2

3，第二层卷积个数从256变为128；三个连续的卷基层，从384-384-256变为256-256-256

4，最后一个pooling层使用SPP pooling方式

5，从半连接两个GPU训练，变成采用全连接的方式单个GPU训练。

本网络大约训练3天，达到了top-5 15.9%的准确率。

3.2 网络的时间复杂度

      d为网络卷积层的总层数，nl为本层卷积filter个数；nl-1为上一层卷积filter个数，也可以称作nl层的输入输入通道数，Sl为filter的尺寸，ml为输出特征图的尺寸

fc层和pooling层的计算复杂度没有计算在内，其计算时间占总时间的5-10%。

上述复杂度只是理论上的，真实的计算时间和部署方式，硬件有关系。

四，层替换设计模型

为了简化模型，本文只考虑阶段内（两个相邻pooling层之间）的平衡；固定阶段内的输入和输出，以便不改变其他层。

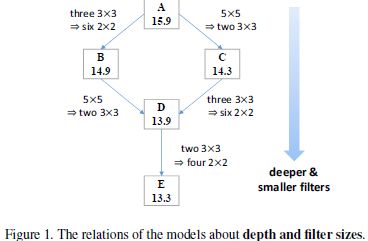
4.1 在深度和filter尺寸上的平衡：把大的filter换成小的filter减小复杂度，增加深度来增加复杂度已达到平衡

B：由于3*3近似等于 2*2+2*2；所以一个256*3*3*256卷基层，近似等于两个256*2*2*256卷基层。

把原始A stage3中的128*3*3*256+256*3*3*256+256*3*3*256的卷基层，替换成128*2*2*256+5个256*2*2*256，这样B就变成了一个有8阶段卷积过程，总网络总共11层的CNN网络。

C: 5*5近似等于3*3+3*3；此外由于A stage2 阶段输入64个特征和输出128个特征，特征个数不相同。所以一个64*5*5*128的卷积过程近似等于64*3*3*128+128*3*3*128.

把A的stage2阶段的5*5filter替换成2个3*3的卷积，从而得到C网络，C有6个卷积层，共计9层网络

D：融合B和C，得到D网络，有9个卷积阶段，总共12层网络。

E：E网络可以看做是把D stage2中的3*3，用2个2*2的替换，即把D stage2中两个3*3的卷提，替换成4个2*2的卷积。也可以看做是用2*2的卷积来替换B的5*5的卷积，只不过进过中间替换步骤D。网络E共有11个卷基层，总共14层。

结果分析：

1，随着网络深度的增加，网络结果越来越好；这可能是增加了非线性能力可以是网络拟合更复杂的函数；也说明网络深度比filter尺寸更重要。

2，B和C的对比中，C的结果比B的好；而B比C网络要更深；说明Astage2中采用5*5的filter，对于结果有不好的影响；所以尽管B网络比C网络更深，但是由于B网络保留了stage2阶段的5*5卷积，所以其结果没有C的好。在filter个数不变的情况下，大的filter尺寸没有多个小的filter好。这个观点和VGG网络中通过多层小的filter尺寸近似一层大的filter会得到更好的结果相似。

4.2深度和宽度的平衡：减少filter个数，减少复杂度；增加深度来增加复杂度来达到平衡。

相比filter和深度的平衡，宽度和深度的平衡比较灵活。特征数目减少的越小，深的就增加的越多。

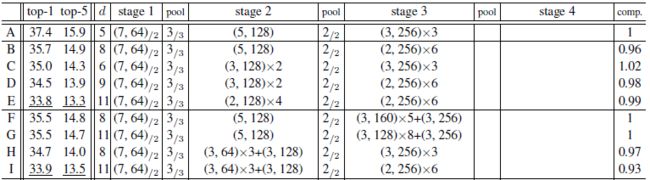
F：把A stage3中128*3*3*256+256*3*3*256+256*3*3*256替换成了128*3*3*160+4个160*3*3*160+160*3*3*256，为了不影响其它层，保持stage3的输入和输出filter个数不变。F共有8个卷基层，共计11层网络。

G：若把stage3中间层卷积filter从256再次降到128，stage3变成了128*3*3*128+8个128*3*3*128+128*3*3*256，这样得到网络G，卷积层有12层，总共15层网络。

H：把网络C的stage2中的2个64*3*3*128+128*3*3*128通过缩小第一个卷积filter到64来增加深度，变成：3个64*3*3*64+64*3*3*128；网络H有8个卷积层，总共11层。

I：把D网络stage2中按照C的方式替换，I网络共有11个卷积层，14层网络

结果分析：

1，分别从A发展而来的网络F（把A的stage3分为6层）和G（把A的stage3分为8层）都比A的结果好，H比C的好，I的比D的好，说明深度越深，网络性能越好。

2，G和F网络性能差的也不太多，说明随着深度的增加网络性能逐渐饱和。

4.3 宽度和filter尺寸的平衡

B：A stage3中的三个卷基层，通过缩小filter尺寸替换成6层：128*2*2*256+5个256*2*2*256，

F：A stage3中的三个卷基层，通过缩小filter个数，替换成6层：128*3*3*160+4个160*3*3*160+160*3*3*256

所以B和F对比，相当于把3*3的filter尺寸换成2*2的，同时增加了filter的个数。

同理E和I网络，把A的stage2分解了成了相同层数，不同的filter尺寸和个数。

B和F，E和I的结果基本一样，说明filter的尺寸和宽度之间优先级差不多，发挥的作用都没有深度大。

4.4越深越好？

试验中持续增加深度时，网络性能会饱和甚至会降低。这里有两个可能的原因：1，过度的减少filter的尺寸和个数可能损害网络性能；2，如果其他的因素不平衡，过度地增加深度导致网络识别率下降。

通过在D的最后一个卷基层添加额外的256 2*2的卷积层，网络其他结构不变，所以每增加一层，都会增加计算时间。实验结果如图

当filter个数和尺寸都不改变时，增加网络的深度会导致网络的性能饱和甚至降低（这个不是因为过拟合，因为训练误差也在增加），所以在固定复杂度下，降低filter尺寸和个数来换取深度的增加，应该有个限度。

此外作者还利用Network in Network中的方法，在B和D的每个卷基层后面增加一个1*1的卷基层来增加网络的深度，发现结果变得有些差，所以再一次证明过度的增加层数，会损害网络性能。

4.5增加pooling 层：特征图尺寸和filter个数的平衡

   本文通过在stage3中插入一个pooling层，然后在新形成的stage4中增加宽度来达到特征图尺寸和filter个数的平衡。

J：stage2的输出特征图大小（stage3的输入维数）维数为17*17或者18*18，然后直接应用spp，现加入一个3*3的pooling层后就变成了5*5或者6*6，在应用spp。维数上降低的复杂度，通过增加filter个数来补偿。

所以网络E 的stage3中最后两个256*2*2*256卷积层中前加入3*3的pooling后，最后两个256*2*2*256卷积层变成新的stage4，filter个数增加为：256*2*2*2304+2304*2*2*256;从而得到网络J。

J的top-5结果为12.5%比E提升了近1%。说明filter个数的增加也可以增加网络性能。

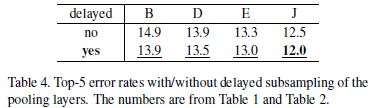
4.6 Pooling层的延迟采样

Pooling层主要起两个作用：1，侧面抑制，以增大局部不变形

2，通过子采样来减小降维

本文通过在max-pooling层的间隔s=1，让其后面的卷积曾间隔s>1的方法，把pooling层的作用分开。在BDEJ网络上实验得结果普遍提升。

五，部署细节

数据增益：和SP-net相同，参数设置也和SPP-net相同。

六，比较

由于不同过的数据增益技术对于结果有影响，所以为了公平；测试的模型使用相同的数据增益技术。

本文的J’网络，每个批次的训练时间为0.41秒，per view的测试时间为1毫秒。

作者对比了ZF-net，OverFeat等网络模型，比这些网络的快速版本还快，而且准确；但是对比VGG和GoogLeNet结果就要差一些，但是计算速度分别快20倍和2.1倍。（VGG使用了一些其他的数据增益技术，GoogLeNet中inception模型不适合GPU但是适合cpu处理）

七，未来工作

深度模型需要占用更大的内存，在未来探讨在限定内存下的最优化网络结构。

一些理解和困惑

感觉本的出发点很好，在限定时间（复杂度内）探索最优化的网络结构；作者首先给予ZF-net或者Alex-net提出了一个效果不错的网络结构A；然后在A的技术上通过stage替换思想来比较层数，filter尺寸和filter个数的优先级；不仅提出在限定时间内的网络结构，更有助于我们了解卷积网络，为以后设计调整深度网络提供了很好的参考。作者的结论和上一篇利用循环卷积网络探索卷积特性的结论相似，深度很重要，深度会饱和，也会溢出。

文中从J到J’网络时，作者探讨了延迟pooling结构，结果有明显的提升，但是作者貌似并没解释这个是为什么，也可能是我没看懂，这个地方有个疑惑。还有就是作者利用Network IN Network的思想，给每个卷积层都增加1*1的新卷基层，层数增加多了，参数也就会增加很多，结果不好感觉像是过拟合引起的；如果增加的少一些层结果可能会好（个人见解）。