最短路算法总结(超详细~)
文章目录
- 最短路算法框架
- 朴素Dijkstra算法
- 堆优化版Dijkstra算法
- Bellman-Ford算法
- SPFA算法
- SPFA判断负环
- Floyd算法
最短路算法框架
最短路有五种算法,分别适用不同的情况。

单源最短路: 求一个点到其他点的最短路
多源最短路: 求任意两个点的最短路
稠密图用邻接矩阵存,稀疏图用邻接表存储。
稠密图: m 和 n2 一个级别
稀疏图: m 和 n 一个级别
朴素Dijkstra算法

集合s:所有已经确定最短路的点
①的意思就是在集合s外找一个距离起点最近的点
②的意思就是让这个最近点放到集合 s 中
Dijkstra算法是通过 n 次循环来确定 n 个点到起点的最短路的。
首先找到一个没有确定最短路且距离起点最近的点,并通过这个点将其他点的最短距离进行更新。每做一次这个步骤,都能确定一个点的最短路,所以需要重复此步骤 n 次,找出 n 个点的最短路。
核心代码
for(int i=0; i<n; i++)
{
int t = -1;
for(int j=1; j<=n; j++) // 在没有确定最短路中的所有点找出距离最短的那个点 t
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t=j;
st[t]=true; // 代表 t 这个点已经确定最短路了
for(int j=1; j<=n; j++) // 用 t 更新其他点的最短距离
dist[j] = min(dist[j],dist[t]+g[t][j]);
}
代码讲解:
① 找到 t 后,t 是剩余未确定最短路中的距离起点最小的结点,那么它的最短距离我们就可以确定了,标记时让 st[t] = true 即可。
② t 是怎样更新其他点的最短距离呢?看下图
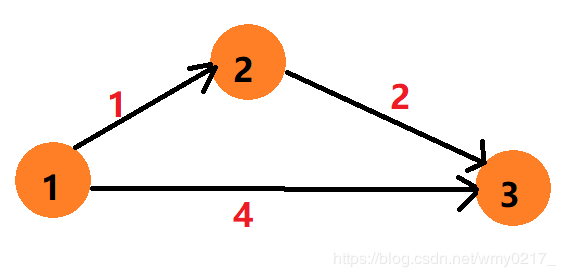
刚开始,t = 1,因为结点 1 距离起点距离为0,是距离最小的,我们拿1这个结点来更新其他结点的最短路,结点 2 的最短路可以更新为 1,因为 t 到起点的距离为 0,而1——>2的距离为 1,0+1=1,同理,结点 3 的最短距离更新为 4 。
这第一个结点的最短距离我们已经确定了,此时,再找下一个 t ,很明显,t = 2,我们再来用 2 这个结点来更新其他点的最短距离,因为 dist[2]+g[2][3] = 1 + 2,很明显 1 + 2 < 4,我们可以把结点 3 的最短距离更新成 3, 对应代码里的 dist[j] = min(dist[j],dist[t]+g[t][j]) 。
代码里每次更新都是循环1~n个结点,其实已经确定最短路的点是不用更新的了,还有 t 这个点可能与 j 这个点间是没有路的,也是不用更新的,不过这不影响答案,但你也可以更新时加个 if(!st[j] && g[t][j]!=0x3f3f3f3f)。
例题:
给定一个n个点m条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出1号点到n号点的最短距离,如果无法从1号点走到n号点,则输出-1。
输入格式
第一行包含整数n和m。
接下来m行每行包含三个整数x,y,z,表示存在一条从点x到点y的有向边,边长为z。
输出格式
输出一个整数,表示1号点到n号点的最短距离。
如果路径不存在,则输出-1。
数据范围
1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
#include堆优化版Dijkstra算法
优化版的Dijkstra算法是通过小根堆来找到当前堆中距离起点最短且没有确定最短路的那个点。
因为是稀疏图,所以需要用邻接表来存储。
还是上到题的题目,只不过数据范围变成1≤n,m≤1.5×105,这个数据范围如果还用朴素算法的话,O(n2)是1010级别,必定超时的,所以我们采用堆优化版的算法。
#include因为题目上是有重边的情况的,假设1——>2是有权重为2和3的重边,我们在用1号结点更新2号结点时,2号结点会两次入堆,这样我们发现堆中会有很多冗余的点,当堆中弹出下一个 t 时,t 是为{2,2}的,而不是{2、3},因为 2<3 ,这个时候我们就可以标记 2 结点为true了,等到下次堆中弹出{2、3}时,我们不需要用{2、3}来更新其他点了,因为我们已经用{2、2}这个距离更小的点更新过了,所以堆中当弹出{2、3}时直接continue即可。
解释一下Dijkstra算法为什么不能用于有负权的边的图:

因为Dijkstra算法是通过当前离起点最近的点来更新其他的点的距离,例如上图中的 4 号结点会被 2 号结点更新为2+1=3,但实际上4号结点的最短路径是3+(-2)=1,这样你就知道为什么Dijkstra算法不能用于有负权的边的图吧。
Bellman-Ford算法
Bellman-Ford算法是通过循环 n 次,每次循环都遍历每条边,进而更新结点的距离,每一次的循环至少可以确定一个点的最短路,所以循环 n次,就可以求出 n 个点的最短路。

for(int i=0; i<n; i++)
for(int j=0; j<m; j++)
{
if(dist[a]+w<dist[b])
dist[b] = dist[a] + w; //w是a->b的权重
}
在这个算法上延申,如果我们想求有边数限制的最短路怎么求呢,假如让求从1号点到n号点的最多经过k条边的最短距离怎么求呢???
需要注意的是我们需要一个备份,先来看看为什么…

还是这张图,假设我们限制边数 k 为 1,那么外层循环只需要进行一次,肉眼可以看出,我们只能求出 1 和 2 和 3号结点的最短路,4号结点最短路是不存在的,可是当在枚举所有条边时,假如我们先枚举的1——>2边时,那么2号结点最短路被更新为2,这是没问题的,可是,当我们再枚举到2——>4边时,4号结点最短路会被更新为2+1=3,如果4后面还有结点的话,后面的所有结点都会被更新,可实际上,4结点是不存在最短路的,因为我们限制了 k。那么怎么解决呢,其实很简单,我们只需要用上一次的dist来更新即可,而我们把上一次更新后的dist放到备份里存起来以备下一次更新用。
有了备份,当枚举1——>2到时,2结点被更新为2,而枚举到2——>4时,4号结点是用2号结点上一次的dist来更新的,而2号结点上一次dist是 +∞,而 +∞ + 1 > +∞,所以说4号结点是不会被更新的。
但是你可能有疑问,2——>4的权值如果是-1,那3号结点是可以更新成 +∞ - 1的,那它不还是更新了?它确实更新了,但是,我们在最后判断时,还是会判断4号没有最短路的,这也就是为什么下道例题最后判断条件写成if(dist[n] > 0x3f3f3f3f/2) return -1。
例题:
853. 有边数限制的最短路
给定一个n个点m条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出从1号点到n号点的最多经过k条边的最短距离,如果无法从1号点走到n号点,输出impossible。
注意:图中可能 存在负权回路 。
输入格式
第一行包含三个整数n,m,k。
接下来m行,每行包含三个整数x,y,z,表示存在一条从点x到点y的有向边,边长为z。
输出格式
输出一个整数,表示从1号点到n号点的最多经过k条边的最短距离。
如果不存在满足条件的路径,则输出“impossible”。
数据范围
1≤n,k≤500,
1≤m≤10000 ,
任意边长的绝对值不超过10000。
输入样例:
3 3 1
1 2 1
2 3 1
1 3 3
输出样例:
3
#includeSPFA算法
SPFA算法需要图中没有负环才能使用。其实大部分正权图也是可以用SPFA算法做的,例如最上面的那到题就可以用SPFA做,效率还高于Dijkstra算法。
SPFA算法是在Bellman-Ford的基础上优化后的算法。在Bellman-Ford算法中,如果某个点未被更新过,我们还是会用这个点去更新其他点,其实,该操作是不必要的,我们只需要拿更新过后的点去更新其他的点,因为只有用被更新过的点更新其他结点x,x的距离才可能变小。
int spfa()
{// bool st[N]: 存第 i 个点是不是在队列中,防止存重复的点
memset(dist,0x3f,sizeof(dist));
dist[1] = 0;
queue<int> q; //存储所有待更新的点
q.push(1); // 1号点入队
st[1] = true;
while(q.size()) // 队列不空
{
int t = q.front(); //取队头
q.pop();
st[t] = false; // 代表这个点已经不在队列了
for(int i = h[t]; i!=-1; i=ne[i]) // 更新 t 的所有临边结点的最短路
{
int j = e[i];
if(dist[j] > dist[t]+w[i])
{
dist[j] = dist[t] + w[i];
if(!st[j]) //如果 j 不在队列,让 j 入队
{
q.push(j);
st[j] = true; // 标记 j 在队中
}
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1; // 不存在最短路
return dist[n];
}
SPFA判断负环
什么是负环呢? 下图左边的2——>3——>4就是一个负环,因为转一圈后的距离是负的,右图的 1 结点是应该自环,也属于负环。
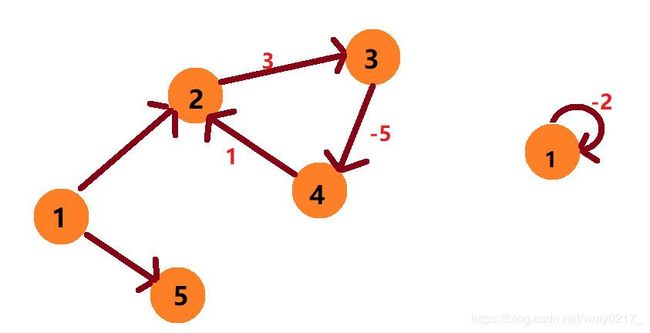
相比上一个代码,多了一个cnt数组,cnt[x] 代表起点到x最短路所经的边数,当 cnt[x] ≥ n 时,则说明 1——>x 这条路径上至少经过 n 条边 ,那么也就是 1——>x 这条路径上至少经过 n+1 个点,而我们知道总共只有 n 个点,说明至少存在两个点是重复经过的,那么这个点构成的环一定是负环,因为只有负环才会让dist距离变小,否则我们为什么要两次经过同一个点呢。
int spfa()
{
queue<int> q;
for(int i=1; i<=n; i++) //将所有结点入队
{
st[i] = true;
q.push(i);
}
while(q.size()) // 队列不空
{
int t = q.front(); //取队头
q.pop();
st[t] = false; // 代表这个点已经不在队列了
for(int i = h[t]; i!=-1; i=ne[i]) // 更新 t 的所有临边结点的最短路
{
int j = e[i];
if(dist[j] > dist[t]+w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1; // t到起点的边数+1
if(cnt[j] >= n) return true;// 存在负环
if(!st[j]) //如果 j 不在队列,让 j 入队
{
q.push(j);
st[j] = true; // 标记 j 在队中
}
}
}
}
return false;// 不存在负环
}
刚开始我们需要让所有点都入队,因为 1 这个结点可能跟我们要找的负环是不连通的,这样的话只通过 1 来是无法判断的,所以,我们让所有结点都入队。
dist数组是否初始化在这里是不影响的,因为我们要求的是是否存在负环,不是距离。
Floyd算法
Floyd算法是基于动态规划的,从结点 i 到结点 j 的最短路径只有两种:
1、直接 i 到 j
2、i 经过若干个结点到 k 再到 j
对于每一个k,我们都判断 d[i][j] 是否大于 d[i][k] + d[k][j],如果大于,就可以更新d[i][j]了。
void floyd()
{
for(int k=1; k<=n; k++)
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
三次循环完之后,遍历完所有的 k 后,d[i][j] 存的就是 i——>j的最短路了。
内容若有不对,还望大佬指正
