Prophet模型预测商品销售量

机器学习训练营（入群联系qq：2279055353）—— 机器学习案例详解的直播互动平台
下期直播案例预告：大数据预测商品的销售量波动趋势

案例介绍

像沃尔玛、家乐福这样的超市零售商，使用销售预报系统和工具补充商品。一套完善的预报系统有助于赢得其它的供应链渠道。如果你擅长预测商品未来一段时间的销量，你就能合理地安排你的库存盘点和分类。

该案例要求根据提供的2013年至2017年商店-商品的销售数据，使用时间序列技术，预测10家不同的商店的50种不同的商品在未来3个月的销售量。

• 数据来源：Kaggle 竞赛

• 代码实现：R 语言

数据文件

训练集train.csv与检验集test.csv. 请到以下百度网盘下载：

链接：https://pan.baidu.com/s/1j2FCvikgR2aPkfW2bDtLsA 密码：mmby

加载R包

首先，加载必需的R包。

rm(list=ls())

suppressMessages(library(data.table))
suppressMessages(library(DT))
suppressMessages(library(timeSeries))
suppressMessages(library(tidyverse))
suppressMessages(library(reshape))
suppressMessages(library(stringr))
suppressMessages(library(doBy))
suppressMessages(library(formattable))
suppressMessages(library(gridExtra))

suppressMessages(library(ggplot2))
suppressMessages(library(plotly))
suppressMessages(library(corrplot))
suppressMessages(library(wesanderson))
suppressMessages(library(RColorBrewer))
suppressMessages(library(gridExtra))
suppressMessages(library(zoo))

suppressMessages(library(forecast))
suppressMessages(library(prophet)) 

set.seed(2018)

加载数据集

train=fread("e:/kaggle_exercises/forecast/input/train.csv")
sprintf("The train data set has %d rows and %d columns", nrow(train), ncol(train) )
str(train)

test  <- fread("e:/kaggle_exercises/forecast/input/test.csv")
sprintf("The test data set has %d rows and %d columns", nrow(test), ncol(test) )
str(test)

print("the summary of train sales is:")
summary(train$sales)

从变量date里提取“年、月”变量

# Extraction of Year and Month of Year :
train$Year=year(train$date)        #returns the year from date i.e. 2013, 2014 etc.
train$Month=as.yearmon(train$date) #this yearmon() function is coming from zoo package returns the month of an year i.e Jan 2013, Feb 2015 etc
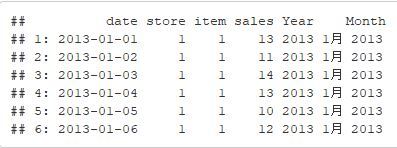
head(train)

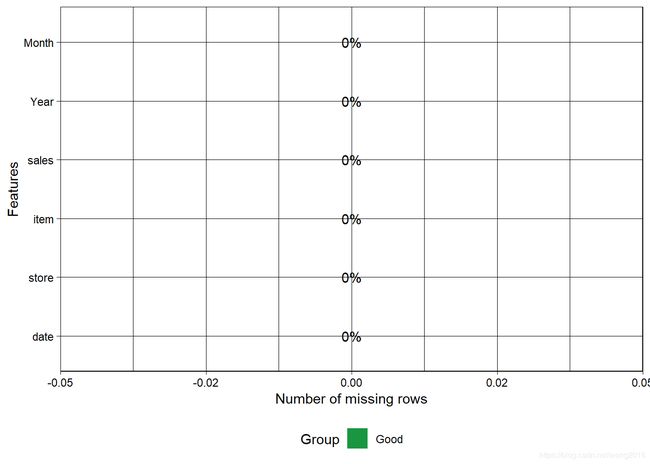
缺失值检查

colSums(is.na(train))
# Function 1 : For ploting missing value
plot_missing <- function(data, title = NULL, ggtheme = theme_gray(), theme_config = list("legend.position" = c("bottom"))) {
  ## Declare variable first to pass R CMD check
  feature <- num_missing <- pct_missing <- group <- NULL
  ## Check if input is data.table
  is_data_table <- is.data.table(data)
  ## Detect input data class
  data_class <- class(data)
  ## Set data to data.table
  if (!is_data_table) data <- data.table(data)
  ## Extract missing value distribution
  missing_value <- data.table(
    "feature" = names(data),
    "num_missing" = sapply(data, function(x) {sum(is.na(x))})
  )
  missing_value[, feature := factor(feature, levels = feature[order(-rank(num_missing))])]
  missing_value[, pct_missing := num_missing / nrow(data)]
  missing_value[pct_missing < 0.05, group := "Good"]
  missing_value[pct_missing >= 0.05 & pct_missing < 0.4, group := "OK"]
  missing_value[pct_missing >= 0.4 & pct_missing < 0.8, group := "Bad"]
  missing_value[pct_missing >= 0.8, group := "Remove"][]
  ## Set data class back to original
  if (!is_data_table) class(missing_value) <- data_class
  ## Create ggplot object
  output <- ggplot(missing_value, aes_string(x = "feature", y = "num_missing", fill = "group")) +
    geom_bar(stat = "identity") +
    geom_text(aes(label = paste0(round(100 * pct_missing, 2), "%"))) +
    scale_fill_manual("Group", values = c("Good" = "#1a9641", "OK" = "#a6d96a", "Bad" = "#fdae61", "Remove" = "#d7191c"), breaks = c("Good", "OK", "Bad", "Remove")) +
    scale_y_continuous(labels = comma) +
    coord_flip() +
    xlab("Features") + ylab("Number of missing rows") +
    ggtitle(title) +
    ggtheme + theme_linedraw()+
    do.call(theme, theme_config)
  ## Print plot
  print(output)
  ## Set return object
  return(invisible(missing_value))
}
plot_missing(train)

可见，数据集里没有缺失值。

特征可视化

我们用图形的方式探索训练集里的特征的分布及变化情况。

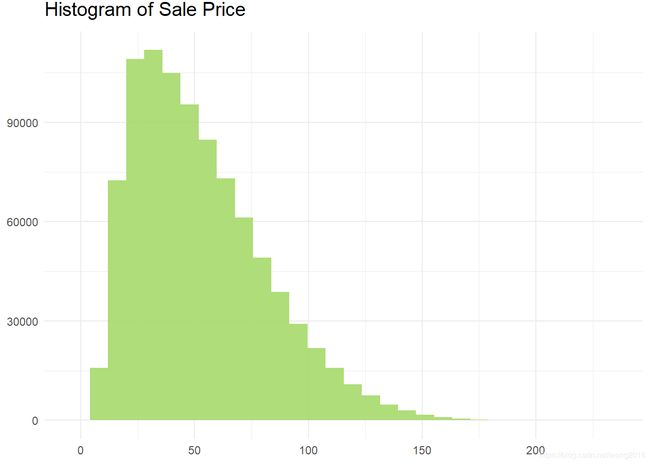
销售量直方图

gbp1<-wes_palette("GrandBudapest2")[1]

ggplot(train, aes(x=sales))+
  geom_histogram(fill="#a6d96a", alpha=.9)+
  labs(x=NULL, y=NULL, title = "Histogram of Sale Price")+
  # scale_x_continuous(breaks= seq(0,600000, by=100000))+
  theme_minimal() + theme(plot.title=element_text(vjust=3, size=15))

从直方图可以看出，销售量的分布是正偏的。

日均销售量与改变率

改变率rate定义为

$$rate=\frac{sale{s}_{i+1}-sale{s}_i}{sale{s}_i},i=0,1,\dots ,t-1$$

MSP <- aggregate(sales ~date, train, mean)
# MSP <-na.omit(ddply(data, 'date', summarise, mean(Sale_Prices, na.rm=T)))

sl1 <-ggplot(MSP, aes(x=as.factor(date), y=sales))+
  geom_line(color=gbp1, aes(group=1), size=1.5)+
  geom_point(colour=gbp1, size = 3.5, alpha=0.5)+
  labs(title="The Growth of Sale Prices by date", x=NULL, y="Sale Price")+
  theme( plot.title=element_text(vjust=3, size=15) ) + theme_minimal()

MSP$rate = c(0, 100*diff(MSP$sales)/MSP[-nrow(MSP),]$sales)

sl2 <-ggplot(MSP, aes(x=as.factor(date), y=rate))+
  geom_line(color= "gray50", aes(group=1), size=1)+
  #geom_point(colour=gbp1, size = 3.5, alpha=0.5)+
  labs(title="Change rate of Sale Price", x="date", y="rate of change")+
  geom_hline(yintercept = 0, color = gbp1 )+
  theme(plot.title=element_text(size=15))+ theme_minimal()

grid.arrange(sl1,sl2)

销售量的改变率关于日期是固定的，我们再看看改变率关于年和月的变化，先来看看关于月份的变化。

MSP <- aggregate(sales ~Month, train, mean)
# MSP <-na.omit(ddply(data, 'date', summarise, mean(Sale_Prices, na.rm=T)))

sl1 <-ggplot(MSP, aes(x=as.factor(Month), y=sales))+
  geom_line(color=gbp1, aes(group=1), size=1.5)+
  geom_point(colour=gbp1, size = 3.5, alpha=0.5)+
  labs(title="The Growth of Sale Prices by Month of Year", x=NULL, y="Sale Price")+
  theme( plot.title=element_text(vjust=3, size=15) ) + theme_minimal()

MSP$rate = c(0, 100*diff(MSP$sales)/MSP[-nrow(MSP),]$sales)

sl2 <-ggplot(MSP, aes(x=as.factor(Month), y=rate))+
  geom_line(color= "gray50", aes(group=1), size=1)+
  #geom_point(colour=gbp1, size = 3.5, alpha=0.5)+
  labs(title="Change rate of Sale Price", x="Month", y="rate of change")+
  geom_hline(yintercept = 0, color = gbp1 )+
  theme(plot.title=element_text(size=15))+ theme_minimal()

grid.arrange(sl1,sl2)

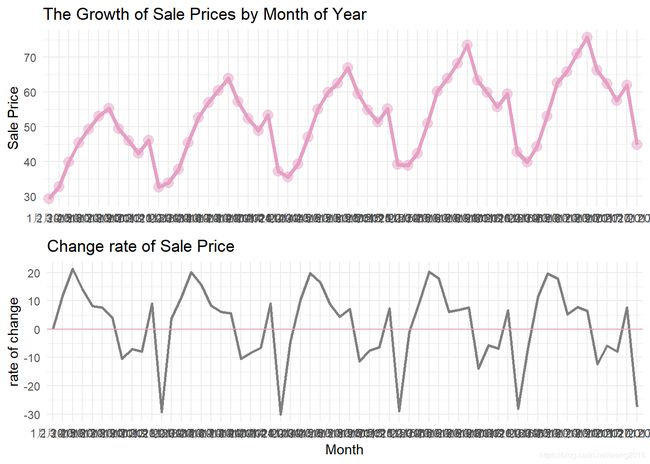
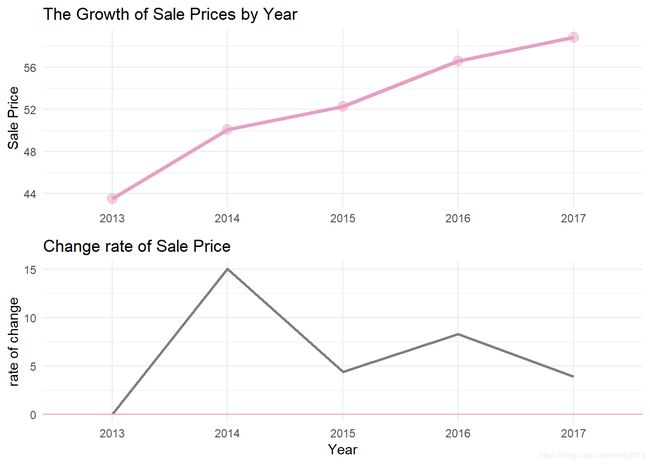
改变率关于月份呈周期性的波动变化，再来看看关于年份的变化情况。

MSP <- aggregate(sales ~Year, train, mean)
# MSP <-na.omit(ddply(data, 'date', summarise, mean(Sale_Prices, na.rm=T)))

sl1 <-ggplot(MSP, aes(x=as.factor(Year), y=sales))+
  geom_line(color=gbp1, aes(group=1), size=1.5)+
  geom_point(colour=gbp1, size = 3.5, alpha=0.5)+
  labs(title="The Growth of Sale Prices by Year", x=NULL, y="Sale Price")+
  theme( plot.title=element_text(vjust=3, size=15) ) + theme_minimal()

MSP$rate = c(0, 100*diff(MSP$sales)/MSP[-nrow(MSP),]$sales)

sl2 <-ggplot(MSP, aes(x=as.factor(Year), y=rate))+
  geom_line(color= "gray50", aes(group=1), size=1)+
  #geom_point(colour=gbp1, size = 3.5, alpha=0.5)+
  labs(title="Change rate of Sale Price", x="Year", y="rate of change")+
  geom_hline(yintercept = 0, color = gbp1 )+
  theme(plot.title=element_text(size=15))+ theme_minimal()

grid.arrange(sl1,sl2)

我们可以得到4点结论：

• 销售量逐年增长；

• 销售量的年改变率呈“高-低”式的波动；

• 从2013年到2014年，改变率单调增加，而从2014到2015年又单调下降；

• 最高的增长率出现在2014年；

• 按这种波动规律，我们推测在2018年改变率是增加的。

不同商店的销售量

我们看看不同的商店的销售量情况，训练集有多少家商店呢？

unique(train$store)

我们再画出这10家商店从2013年到2017年的销售量。

Year_state<-aggregate(sales ~store+Year, train,mean)
pal<-rep(brewer.pal(10, "BrBG"),5)

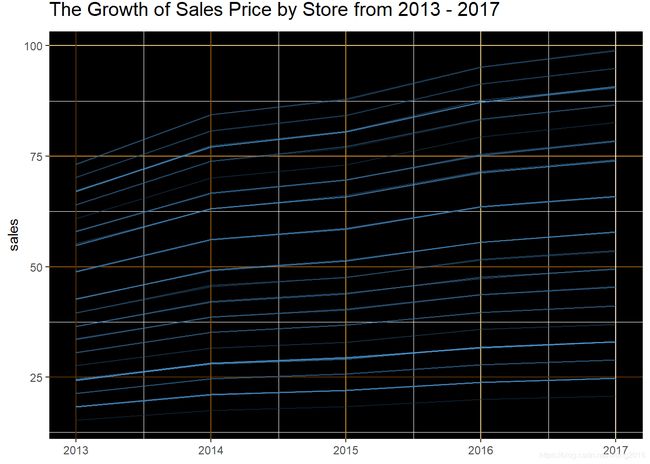
ggplot(Year_state, aes(group = store ))+
  geom_line(aes(x=Year,y=sales,color=store), alpha=0.5, show.legend=F)+
  labs(title="The Growth of Sales Price by Store from 2013 - 2017", x=NULL
  )+
  theme(panel.background=element_rect(fill = "Black"),
        plot.title=element_text(vjust=3, size=15),
        panel.grid.major=element_line(color = pal))

3号商店有最高的年销售量变化，而7号商店的最低。

不同商品的年销售量

训练集train有多少种商品呢？

unique(train$item)

我们看一看这50种商店年销售量的变化趋势。

Year_state<-aggregate(sales ~item+Year, train,mean)
pal<-rep(brewer.pal(10, "BrBG"),5)

ggplot(Year_state, aes(group = item ))+
  geom_line(aes(x=Year,y=sales,color=item), alpha=0.5, show.legend=F)+
  labs(title="The Growth of Sales Price by Store from 2013 - 2017", x=NULL
  )+
  theme(panel.background=element_rect(fill = "Black"),
        plot.title=element_text(vjust=3, size=15),
        panel.grid.major=element_line(color = pal))

17号商品年销售量最高，26号商品的最低。

Prophet model

Prophet 介绍

Prophet是在一个加性模型的基础上预报时间序列数据。这个加性模型拟合时间序列里的年、周、日、季节、假期效应等趋势。对于有强季节效应的时间序列，Prophet 模型特别有效。Prophet对缺失数据、季节漂移也是稳健的。一个Prophet模型定义为

$$\hat{y}=trend\times (1+multiplicativeterms)+additiveterms$$

Prophet 基础模型

现在，我们产生一个Prophet基础模型：store= 1, Product_ID=1. 即，预报1号商店的1号商品销售量。为此，需要先把这两个变量的观测值进行对数变换。

train_final_store1_item1=subset(train,train$store==1 & train$item==1)

stats=data.frame(y=log1p(train_final_store1_item1$sales)
                 ,ds=train_final_store1_item1$date)
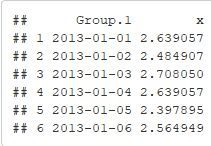
stats=aggregate(stats$y,by=list(stats$ds),FUN=sum)
head(stats)

colnames(stats)<- c("ds","y")
model_prophet = prophet(stats)
summary(model_prophet)

future = make_future_dataframe(model_prophet, periods = 90)
forecast = predict(model_prophet, future)

下面，可视化我们的Prophet model的改变点。

add_changepoints_to_plot <- function(m, threshold = 0.01, cp_color = "red",
                               cp_linetype = "dashed", trend = TRUE, ...) {
  layers <- list()
  if (trend) {
    trend_layer <- ggplot2::geom_line(
      ggplot2::aes_string("ds", "trend"), color = cp_color, ...)
    layers <- append(layers, trend_layer)
  }
  signif_changepoints <- m$changepoints[abs(m$params$delta) >= threshold]
  cp_layer <- ggplot2::geom_vline(
    xintercept = as.integer(signif_changepoints), color = cp_color,
    linetype = cp_linetype, ...)
  layers <- append(layers, cp_layer)
  return(layers)
}
plot(model_prophet, forecast)+ add_changepoints_to_plot(model_prophet)

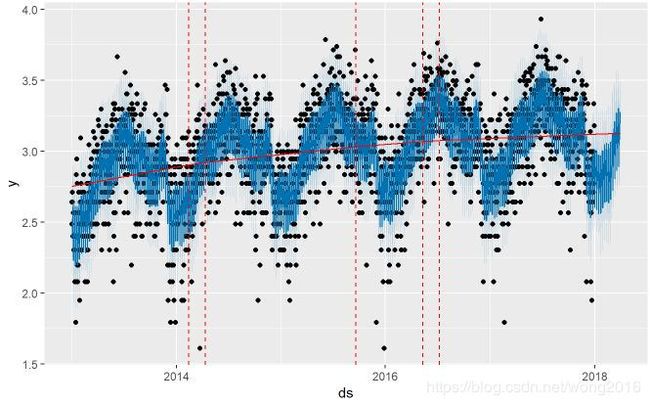
图中红线标记的是改变点，我们需要删除多个改变点，这是由于模型过度拟合造成的。

我们再检查一下模型成分：

prophet_plot_components(model_prophet, forecast)

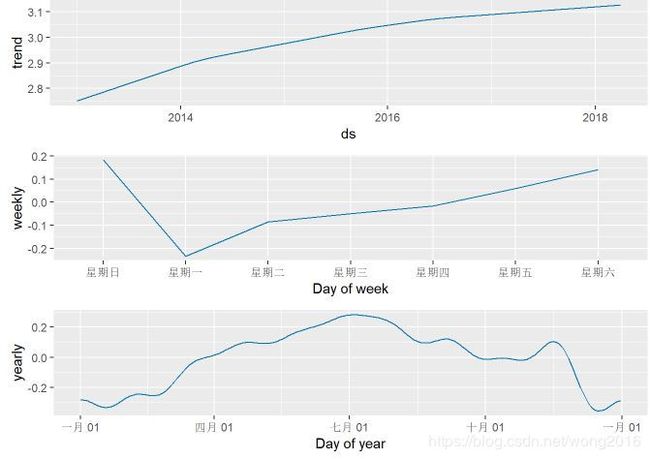
我们发现，从周日到周一销售量明显下降。因此在销售数据里一定有假日效应。在7月份有一个销售量高峰，这意味着假日时间或者打折促销的影响。综合这些分析，我们认为有必要优化Prophet参数，尝试排除改变点，包括假日效应。