PyTorch之四—梯度下降 和 关系拟合
文章目录
- PyTorch梯度传递
- 线性、多项式模型
- 线性回归示例
- 多项式回归示例
PyTorch梯度传递
在PyTorch中,传入网络计算的数据类型必须是 Variable 类型, Variable包装了一个Tensor,并且保存着梯度和创建这个Variable function的引用,换句话说,就是记录网络每层的梯度和网络图,可以实现梯度的反向传递。
整体网络图如下:
i n p u t → c o n v 2 d → r e l u → m a x p o o l 2 d → c o n v 2 d → r e l u → m a x p o o l 2 d → v i e w → l i n e a r → r e l u → l i n e a r → r e l u → l i n e a r → M S E L o s s → l o s s \begin{aligned} \sf input \to & \sf conv2d \to relu \to maxpool2d \to conv2d\to relu\to maxpool2d \\ \to & \sf view \to linear \to relu \to linear \to relu \to linear\\ \to & \sf MSE Loss \\ \to & \sf loss \end{aligned} input→→→→conv2d→relu→maxpool2d→conv2d→relu→maxpool2dview→linear→relu→linear→relu→linearMSELossloss
则根据最后得到的loss可以逐步递归的求其每层的梯度,并实现权重更新。
在实现梯度反向传递时主要需要三步:
- 初始化梯度值:
net.zero_grad() - 反向求解梯度:
loss.backward() - 更新参数:
optimizer.step()
线性、多项式模型
pytorch 我们以一个简单的线性回归开始深度学习。这是一个非常简单的模型,线性回归。对模型进行优化,用到梯度下降法。
一元线性模型非常简单,假设我们有变量 x i x_i xi 和目标 y i y_i yi ,每个 i i i 对应于一个数据点,建立一个模型 y ^ i = w x i + b \hat{y}_i=wx_i+b y^i=wxi+b。
整个过程是:通过 y ^ i \hat{y}_i y^i (预测结果)来拟合目标 y i y_i yi, 通俗来讲就是找到这个函数拟合 y i y_i yi 使得误差最小:
即最小化 1 n ∑ i n = ( y ^ i − y i ) 2 \frac{1}{n} \sum_i^n = (\hat{y}_i-y_i)^2 n1∑in=(y^i−yi)2
那么如何最小化这个误差呢? 这里需要用到梯度下降,这是我们接触到的第一个优化算法,非常简单,但是却非常强大,在深度学习中被大量使用。关于梯度下降算法请点击
线性回归示例
import torch
from torch.autograd import Variable
import torch.nn.functional as F
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-1,1,200),dim=1) # shape=(100,1)
y = 2*x + 0.5*torch.rand(x.size())+5 # noisy y data(tensor) ,shape=(100,1)
# 用Variable修饰tensor
x,y = torch.autograd.Variable(x),Variable(y)
####################### 搭建神经网络 ###########################
class Net(torch.nn.Module):
def __init__(self,n_feature,n_hidden,n_output):
super(Net,self).__init__() # 继承 __init__ 功能
self.hidden = torch.nn.Linear(n_feature,n_hidden)
self.predict = torch.nn.Linear(n_hidden,n_output)
def forward(self, x): # 这同时也是Module中的forward功能
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.predict(x) # 输出值
return x
net = Net(n_feature=1,n_hidden=10,n_output=1)
print("输出网络结构net:",net)
# 训练网络(优化工具:梯度下降方法和损失函数)
optimizer = torch.optim.SGD(net.parameters(),lr=0.05) # 传入net的所有参数,学习率
loss_func = torch.nn.MSELoss() # 预测值和真实值的误差公式(均方差)
plt.ion() # 开启可视化训练过程
for step in range(100):
prediction = net(x) # 喂给net训练数据x,输出预测值
loss = loss_func(prediction,y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
if step%20 ==0:
print("loss",loss.data)
plt.cla()
plt.scatter(x.data.numpy(),y.data.numpy())
plt.plot(x.data.numpy(),prediction.data.numpy(),"r-",lw=3)
# plt.text(0.5,0,"Loss=%.4f"%loss.data,fontdict={'size':20,'color':'red'})
plt.pause(0.1)
plt.ioff()
plt.show()
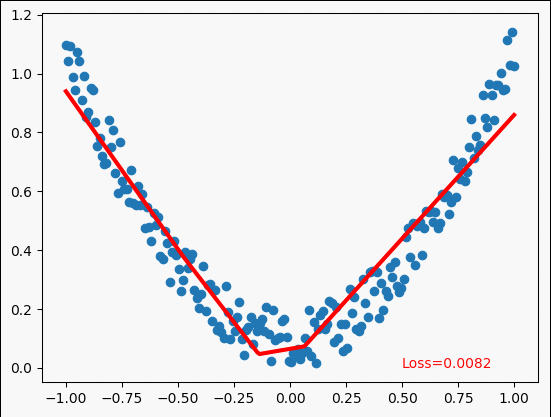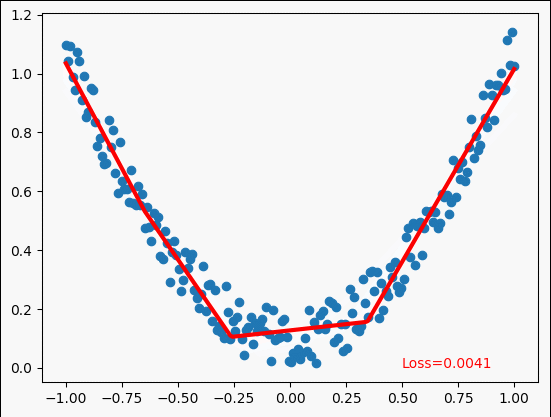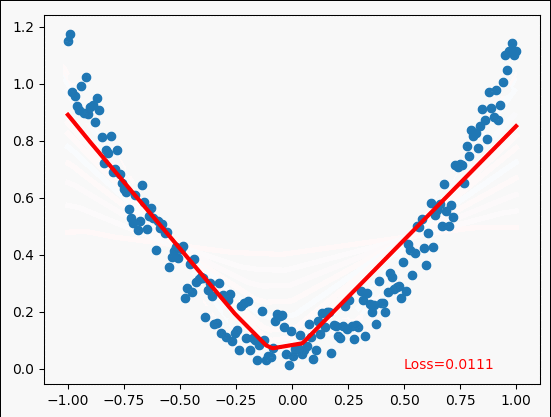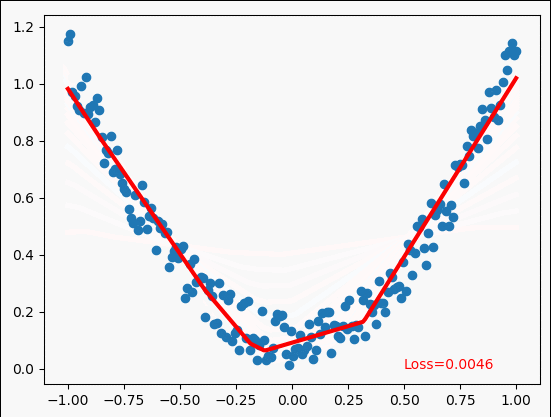
多项式回归示例
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
import torch.nn.functional as F
x = torch.unsqueeze(torch.linspace(-1,1,200),dim=1) # shape=(100,1)
y = x**2 + 0.2*torch.rand(x.size()) # noisy y data(tensor) ,shape=(100,1)
# 用Variable修饰tensor
x,y = torch.autograd.Variable(x),Variable(y)
# 绘图
# plt.scatter(x.data.numpy(),y.data.numpy())
# plt.show()
####################### 搭建神经网络 ###########################
class Net(torch.nn.Module):
def __init__(self,n_feature,n_hidden,n_output):
super(Net,self).__init__() # 继承 __init__ 功能
self.hidden = torch.nn.Linear(n_feature,n_hidden)
self.predict = torch.nn.Linear(n_hidden,n_output)
def forward(self, x): # 这同时也是Module中的forward功能
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.predict(x) # 输出值
return x
net = Net(n_feature=1,n_hidden=10,n_output=1)
print("输出网络结构net:",net)
# 训练网络(优化工具:梯度下降方法和损失函数)
optimizer = torch.optim.SGD(net.parameters(),lr=0.05) # 传入net所有参数,学习率(不可太高)
loss_func = torch.nn.MSELoss() # 预测值和真实值的误差公式(均方差)
plt.ion() # 开启可视化训练过程
for step in range(5000):
prediction = net(x) # 喂给net训练数据x,输出预测值
loss = loss_func(prediction,y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
if step%100 ==0:
print("loss",loss.data)
plt.cla()
plt.scatter(x.data.numpy(),y.data.numpy())
plt.plot(x.data.numpy(),prediction.data.numpy(),"r-",lw=3)
plt.text(0.5,0,"Loss=%.4f"%loss.data,fontdict={'size':10,'color':'red'})
plt.pause(0.1)
plt.ioff()
plt.show()
输出:
输出网络结构net: Net(
(hidden): Linear(in_features=1, out_features=10, bias=True)
(predict): Linear(in_features=10, out_features=1, bias=True)
)
鸣谢
https://blog.csdn.net/qjk19940101/article/details/79561471