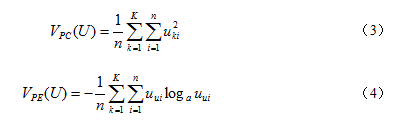Python :k-means聚类算法对数据进行分类
K均值聚类算法,基于目标最小化策略算法可以首先从给定的数据集中,随机选择k个数据对象作为k个簇的初始聚类中心,且每个聚类中心点对应于一个聚类;对剩余的数据对象,计算它们与各个簇中心点的距离,将它们指派到离其最近的簇中;最后,重新计算各个簇中的中心点。按照上述过程进行重复计算,直到聚类中心点不再发生变化或者目标准则函数收敛到一个最佳的位置处。该算法所采用的目标函数一般为如式(1)和式(2)所示:
其中,为第j个簇中数据对象的中心心点,为簇所包含的数据对象。由此可得,目标函数J是关于簇中的数据对象与簇中心点之间的函数,该算法就是试图找到令目标函数J取得最小值时的k值,按照这个方法对数据集进行处理,所获得的聚类结果就可以满足簇内紧凑而同时也达到簇间远离的性质。由此可以得到聚类算法的具体步骤如下:
输入:聚类数k,以及所要处理的数据集;
输出:k个簇的划分情况。
Stepl从数据集中随机选取k个数据对象作为k个簇的初始聚类中心点,且每个数据对象对应于一个簇;
Step2将剩余的数据对象根据其与各个簇中心点的距离,分别指派到离其距离最近的簇中;
Step3更新每个簇的聚类中心,即重新计算各个簇内所有对象的平均值;
Step4重新分配各个数据对象;
Step5直到准则函数收敛或者聚类中心不再变化,否则转到step3。
在给定聚类个数范围内,如何利用一个标准去评价同一个算法在不同聚类参数条件下或不同算法所生成的聚类划分的情况,进而选择其中最好的聚类划分结果,这个问题就称为聚类结果评价问题。通常,对数据集的聚类划分情况的有效性评价主要有4类评价标准,分别是外部聚类有效性、内部聚类有效性、相对聚类有效性以及模糊评价有效性。目前,比较常用的评价聚类质量的指标主要有外部和内部聚类有效性。外部聚类有效性是指利用聚类分析算法对数据集进行处理,所得到的聚类划分结果与数据集中的“真实”聚类划分结果进行比较,来对其有效性进行评估。内部聚类有效性是主要考虑数据集自身的几何分布特征来对聚类结果进行评价。
当不知道数据集的真实聚类数的情况下,一般都是使用内部聚类有效性进行评价的。这种方法往往需要使用一些比如统计指标进行衡量聚类质量,聚类有效性指标是其中一类比较常见的指标。下面就介绍一下Bezdek[1]等人提出的和指标。
这两个指标都是基于数据集的模糊划分的有效性指标,它们的基本思想是:一个能够被较好地进行分类的数据集其结构应该是比较分明的。因此,模糊划分的模糊性越小,聚类的结果就越可靠,具体到这两个指标就是,值越大、同时值达到越小时,就认为所得到的聚类结果是比较好的。所以,在利用该指标进行判断时,一般应用模糊聚类算法上时,数据集的聚类划分效果会更显著。
患者编号653个数据,对应的指标1到指标9,分成2类,并与结果做对比
cancer.csv数据表如下(部分):
| 患者编号 | 指标1 | 指标2 | 指标3 | 指标4 | 指标5 | 指标6 | 指标7 | 指标8 | 指标9 | 结果 |
| 1 | 5 | 4 | 3 | 1 | 2 | 2 | 2 | 3 | 1 | 0 |
| 2 | 9 | 1 | 2 | 6 | 4 | 10 | 7 | 7 | 2 | 1 |
| 3 | 10 | 4 | 7 | 2 | 2 | 8 | 6 | 1 | 1 | 1 |
| 4 | 6 | 10 | 10 | 10 | 8 | 10 | 7 | 10 | 7 | 1 |
| 5 | 1 | 1 | 1 | 1 | 2 | 5 | 5 | 1 | 1 | 0 |
| 6 | 7 | 6 | 10 | 5 | 3 | 10 | 9 | 10 | 2 | 1 |
| 7 | 8 | 10 | 10 | 8 | 5 | 10 | 7 | 8 | 1 | 1 |
# -*- coding: utf-8 -*-
#导入相应的包
import scipy
import scipy.cluster.hierarchy as sch
from scipy.cluster.vq import vq,kmeans,whiten
import numpy as np
import matplotlib.pylab as plt
#待聚类的数据点,cancer.csv有653行数据,每行数据有11维:
dataset = np.loadtxt('cancer.csv', delimiter=",")
#np数据从0开始计算,第0维维序号排除,第10维为标签排除,所以为1到9
points = dataset[:,1:9]
cancer_label = dataset[:,10]
print "points:\n",points
print "cancer_label:\n",cancer_label
# k-means聚类
#将原始数据做归一化处理
data=whiten(points)
#使用kmeans函数进行聚类,输入第一维为数据,第二维为聚类个数k.
#有些时候我们可能不知道最终究竟聚成多少类,一个办法是用层次聚类的结果进行初始化.当然也可以直接输入某个数值.
#k-means最后输出的结果其实是两维的,第一维是聚类中心,第二维是损失distortion,我们在这里只取第一维,所以最后有个[0]
#centroid = kmeans(data,max(cluster))[0]
centroid = kmeans(data,2)[0]
print centroid
#使用vq函数根据聚类中心对所有数据进行分类,vq的输出也是两维的,[0]表示的是所有数据的label
label=vq(data,centroid)[0]
num = [0,0]
for i in label:
if(i == 0):
num[0] = num[0] + 1
else:
num[1] = num[1] + 1
print 'num =',num
#np.savetxt('file.csv',label)
print "Final clustering by k-means:\n",label
result = np.subtract(label,cancer_label)
print "result:\n",result
count = [0,0]
for i in result:
if(i == 0):
count[0] = count[0] + 1
else:
count[1] = count[1] + 1
print count
print float(count[1])/(count[0]+count[1])
对应的两个聚类中心
[[ 2.52612843 2.22211052 2.27257816 2.01076645 2.4789527 2.18249504 2.47753082 1.99449756]
[ 1.08112076 0.4182251 0.47620425 0.46259632 0.93896015 0.36498218 0.83720937 0.39867914]]
对应的两个聚类的个数
num = [217, 436]
与对应的结果做对比
[25, 628]
正确率为:0.961715160796
标签的结果分类可能相反,则结果为:
[628, 25]
0.0382848392037
https://github.com/wukai0909/k-means-clustering
[1]Bensaid A M.Validity-Guided(Re) CIustering with Applications to Image Segmentation[J].IEEE Transactions on Fuzzy Systems,1996,4(2):112-123.