Python绘图总结(Matplotlib篇)之图形分类及保存

学习https://matplotlib.org/gallery/index.html 记录，描述不一定准确，具体请参考官网
Matplotlib使用总结图

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号

import pandas as pd
import numpy as np

把图保存为文件

我们可以用plt.savefig来保存图。这个方法等同于直接在figure对象上调用savefig方法。例如，想要保存一个SVG版本的图片，键入：

`plt.savefig('figpath.svg)`

保存的文件类型通过文件名后缀来指定。即如果使用 .pdf做为后缀，就会得到一个PDF文件。这里有一些重要的设置，作者经常用来刊印图片：

• dpi，控制每英寸长度上的分辨率
• bbox_inches, 能删除figure周围的空白部分

比如我们想要得到一幅PNG图，有最小的空白，400 DPI，键入：

plt.savefig('figpath.png', dpi=400, bbox_inches='tight')

savefig不仅可以写入磁盘，还可以导出为任意像是文件一样的对象，比如BytesIO：

from io import BytesIO
buffer = BytesIO()
plt.savefig(buffer)
plot_data = buffer.getvalue()

看下图关于savefig更多的选项：

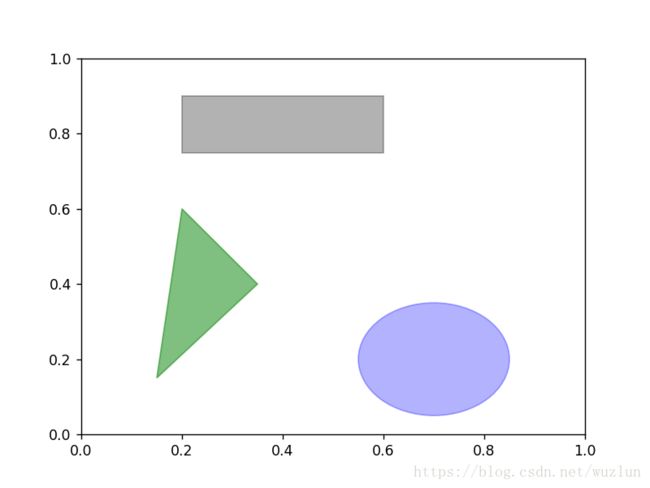
普通图形

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)

rect = plt.Rectangle((0.2, 0.75), 0.4, 0.15, color='k', alpha=0.3)
circ = plt.Circle((0.7, 0.2), 0.15, color='b', alpha=0.3)
pgon = plt.Polygon([[0.15, 0.15], [0.35, 0.4], [0.2, 0.6]],
                   color='g', alpha=0.5)

ax.add_patch(rect)
ax.add_patch(circ)
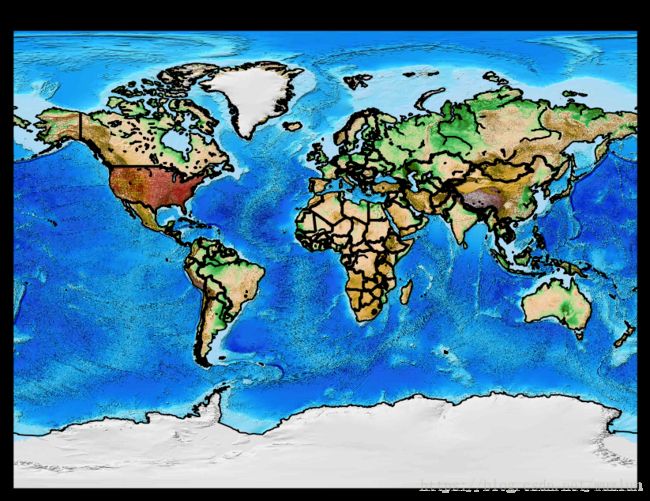
ax.add_patch(pgon)

地图

# 地形
plt.figure(dpi=128, figsize = (8,4))
m = Basemap(projection = 'mill',
            llcrnrlat = -90,  # 左下角的纬度
            llcrnrlon = -180,  # 左下角经度
            urcrnrlat = 90,   # 右上角的纬度
            urcrnrlon = 180,    # 右上角的经度
            resolution ='l'    #分辨率
           )
m.drawcoastlines() 
m.drawcountries(linewidth=2)
m.drawcounties(color='darkred')

m.etopo() #地形
# m.bluemarble()  # 大理石样式

plt.title('Basemap Tutorial')
plt.show()

# 绘制坐标
plt.figure(dpi=128, figsize = (8,4))
m = Basemap(projection = 'mill',
            llcrnrlat = 25,  # 左下角的纬度
            llcrnrlon = -130,  # 左下角经度
            urcrnrlat = 50,   # 右上角的纬度
            urcrnrlon = -60,    # 右上角的经度
            resolution ='l'    #分辨率
)

m.drawcoastlines()
m.drawcountries(linewidth=2)
m.drawstates(color='b')

xs = []
ys = []

# 指定坐标坐五角星
NYClat, NYClon = 40.7127, -74.0059
xpt, ypt = m(NYClon, NYClat)
xs.append(xpt)
ys.append(ypt)
m.plot(xpt, ypt, 'r*', markersize=15)

# 指定坐标坐三角形
LAlat, LAlon = 34.05, -118.25
xpt, ypt = m(LAlon, LAlat)
xs.append(xpt)
ys.append(ypt)
m.plot(xpt, ypt, 'g^', markersize=15)

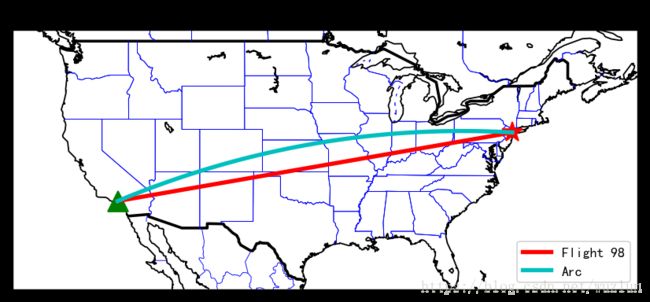
# 画直线
m.plot(xs, ys, color='r', linewidth=3, label='Flight 98')
# 画弧线
m.drawgreatcircle(NYClon, NYClat, LAlon, LAlat, color ='c', linewidth=3, label='Arc')

plt.legend(loc=4)
plt.title('Basemap Tutorial')
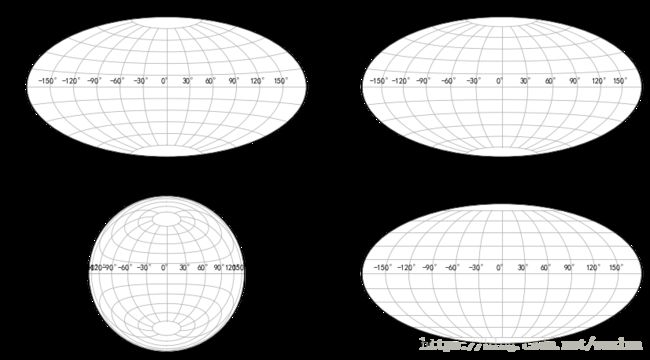
plt.show()

地理相关

# 地理相关
fig = plt.figure(figsize=(14,8))

ax1 = fig.add_subplot(221,  projection="aitoff")
ax1.set_title("Aitoff")
ax1.grid(True)

ax2 = fig.add_subplot(222,  projection="hammer")
ax2.set_title("hammer")
ax2.grid(True)

ax3 = fig.add_subplot(223,  projection="lambert")
ax3.set_title("lambert")
ax3.grid(True)

ax4 = fig.add_subplot(224,  projection="mollweide")
ax4.set_title("mollweide")
ax4.grid(True)

x = np.linspace(0, 2 * np.pi, 400)
y = np.sin(x ** 2)

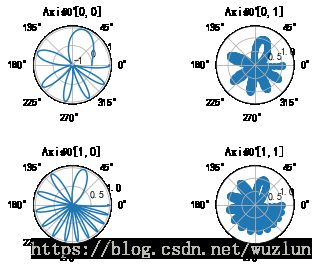
f, axarr = plt.subplots(2, 2, subplot_kw=dict(projection='polar'))
axarr[0, 0].plot(x, y)
axarr[0, 0].set_title('Axis [0,0]')
axarr[0, 1].scatter(x, y)
axarr[0, 1].set_title('Axis [0,1]')
axarr[1, 0].plot(x, y ** 2)
axarr[1, 0].set_title('Axis [1,0]')
axarr[1, 1].scatter(x, y ** 2)
axarr[1, 1].set_title('Axis [1,1]')
# Fine-tune figure; make subplots farther from each other.
f.subplots_adjust(hspace=0.8)

3D

%matplotlib inline

from mpl_toolkits.mplot3d.axes3d import Axes3D
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FixedLocator, FormatStrFormatter
import matplotlib.pyplot as plt
import numpy as np

# 画板大小
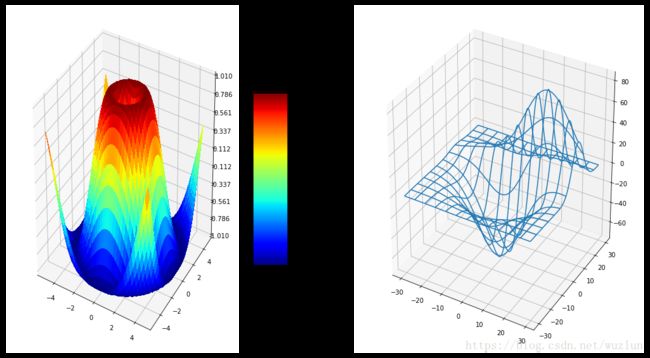
fig = plt.figure(figsize=(18,10))

#画布1
ax = fig.add_subplot(1, 2, 1, projection='3d')
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet,
        linewidth=0, antialiased=False)
ax.set_zlim3d(-1.01, 1.01)

ax.w_zaxis.set_major_locator(LinearLocator(10))
ax.w_zaxis.set_major_formatter(FormatStrFormatter('%.03f'))

# 颜色条
fig.colorbar(surf, shrink=0.5, aspect=5)


#画布2
from mpl_toolkits.mplot3d.axes3d import get_test_data
ax = fig.add_subplot(1, 2, 2, projection='3d')
X, Y, Z = get_test_data(0.05)
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)

plt.show()

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)

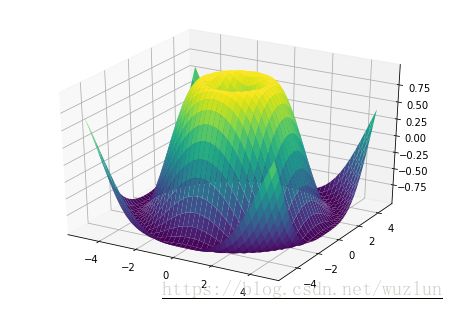
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)

plt.show()

雷达图

%matplotlib inline

import numpy as np

import matplotlib.pyplot as plt
from matplotlib.path import Path
from matplotlib.spines import Spine
from matplotlib.projections.polar import PolarAxes
from matplotlib.projections import register_projection


def radar_factory(num_vars, frame='circle'):
    """Create a radar chart with `num_vars` axes.

    This function creates a RadarAxes projection and registers it.

    Parameters
    ----------
    num_vars : int
        Number of variables for radar chart.
    frame : {'circle' | 'polygon'}
        Shape of frame surrounding axes.

    """
    # calculate evenly-spaced axis angles
    theta = np.linspace(0, 2*np.pi, num_vars, endpoint=False)

    def draw_poly_patch(self):
        # rotate theta such that the first axis is at the top
        verts = unit_poly_verts(theta + np.pi / 2)
        return plt.Polygon(verts, closed=True, edgecolor='k')

    def draw_circle_patch(self):
        # unit circle centered on (0.5, 0.5)
        return plt.Circle((0.5, 0.5), 0.5)

    patch_dict = {'polygon': draw_poly_patch, 'circle': draw_circle_patch}
    if frame not in patch_dict:
        raise ValueError('unknown value for `frame`: %s' % frame)

    class RadarAxes(PolarAxes):

        name = 'radar'
        # use 1 line segment to connect specified points
        RESOLUTION = 1
        # define draw_frame method
        draw_patch = patch_dict[frame]

        def __init__(self, *args, **kwargs):
            super(RadarAxes, self).__init__(*args, **kwargs)
            # rotate plot such that the first axis is at the top
            self.set_theta_zero_location('N')

        def fill(self, *args, **kwargs):
            """Override fill so that line is closed by default"""
            closed = kwargs.pop('closed', True)
            return super(RadarAxes, self).fill(closed=closed, *args, **kwargs)

        def plot(self, *args, **kwargs):
            """Override plot so that line is closed by default"""
            lines = super(RadarAxes, self).plot(*args, **kwargs)
            for line in lines:
                self._close_line(line)

        def _close_line(self, line):
            x, y = line.get_data()
            # FIXME: markers at x[0], y[0] get doubled-up
            if x[0] != x[-1]:
                x = np.concatenate((x, [x[0]]))
                y = np.concatenate((y, [y[0]]))
                line.set_data(x, y)

        def set_varlabels(self, labels):
            self.set_thetagrids(np.degrees(theta), labels)

        def _gen_axes_patch(self):
            return self.draw_patch()

        def _gen_axes_spines(self):
            if frame == 'circle':
                return PolarAxes._gen_axes_spines(self)
            # The following is a hack to get the spines (i.e. the axes frame)
            # to draw correctly for a polygon frame.

            # spine_type must be 'left', 'right', 'top', 'bottom', or `circle`.
            spine_type = 'circle'
            verts = unit_poly_verts(theta + np.pi / 2)
            # close off polygon by repeating first vertex
            verts.append(verts[0])
            path = Path(verts)

            spine = Spine(self, spine_type, path)
            spine.set_transform(self.transAxes)
            return {'polar': spine}

    register_projection(RadarAxes)
    return theta


def unit_poly_verts(theta):
    """Return vertices of polygon for subplot axes.

    This polygon is circumscribed by a unit circle centered at (0.5, 0.5)
    """
    x0, y0, r = [0.5] * 3
    verts = [(r*np.cos(t) + x0, r*np.sin(t) + y0) for t in theta]
    return verts


def example_data():
    # The following data is from the Denver Aerosol Sources and Health study.
    # See  doi:10.1016/j.atmosenv.2008.12.017
    #
    # The data are pollution source profile estimates for five modeled
    # pollution sources (e.g., cars, wood-burning, etc) that emit 7-9 chemical
    # species. The radar charts are experimented with here to see if we can
    # nicely visualize how the modeled source profiles change across four
    # scenarios:
    #  1) No gas-phase species present, just seven particulate counts on
    #     Sulfate
    #     Nitrate
    #     Elemental Carbon (EC)
    #     Organic Carbon fraction 1 (OC)
    #     Organic Carbon fraction 2 (OC2)
    #     Organic Carbon fraction 3 (OC3)
    #     Pyrolized Organic Carbon (OP)
    #  2)Inclusion of gas-phase specie carbon monoxide (CO)
    #  3)Inclusion of gas-phase specie ozone (O3).
    #  4)Inclusion of both gas-phase species is present...
    data = [
        ['Sulfate', 'Nitrate', 'EC', 'OC1', 'OC2', 'OC3', 'OP', 'CO', 'O3'],
        ('Basecase', [
            [0.88, 0.01, 0.03, 0.03, 0.00, 0.06, 0.01, 0.00, 0.00],
            [0.07, 0.95, 0.04, 0.05, 0.00, 0.02, 0.01, 0.00, 0.00],
            [0.01, 0.02, 0.85, 0.19, 0.05, 0.10, 0.00, 0.00, 0.00],
            [0.02, 0.01, 0.07, 0.01, 0.21, 0.12, 0.98, 0.00, 0.00],
            [0.01, 0.01, 0.02, 0.71, 0.74, 0.70, 0.00, 0.00, 0.00]]),
        ('With CO', [
            [0.88, 0.02, 0.02, 0.02, 0.00, 0.05, 0.00, 0.05, 0.00],
            [0.08, 0.94, 0.04, 0.02, 0.00, 0.01, 0.12, 0.04, 0.00],
            [0.01, 0.01, 0.79, 0.10, 0.00, 0.05, 0.00, 0.31, 0.00],
            [0.00, 0.02, 0.03, 0.38, 0.31, 0.31, 0.00, 0.59, 0.00],
            [0.02, 0.02, 0.11, 0.47, 0.69, 0.58, 0.88, 0.00, 0.00]]),
        ('With O3', [
            [0.89, 0.01, 0.07, 0.00, 0.00, 0.05, 0.00, 0.00, 0.03],
            [0.07, 0.95, 0.05, 0.04, 0.00, 0.02, 0.12, 0.00, 0.00],
            [0.01, 0.02, 0.86, 0.27, 0.16, 0.19, 0.00, 0.00, 0.00],
            [0.01, 0.03, 0.00, 0.32, 0.29, 0.27, 0.00, 0.00, 0.95],
            [0.02, 0.00, 0.03, 0.37, 0.56, 0.47, 0.87, 0.00, 0.00]]),
        ('CO & O3', [
            [0.87, 0.01, 0.08, 0.00, 0.00, 0.04, 0.00, 0.00, 0.01],
            [0.09, 0.95, 0.02, 0.03, 0.00, 0.01, 0.13, 0.06, 0.00],
            [0.01, 0.02, 0.71, 0.24, 0.13, 0.16, 0.00, 0.50, 0.00],
            [0.01, 0.03, 0.00, 0.28, 0.24, 0.23, 0.00, 0.44, 0.88],
            [0.02, 0.00, 0.18, 0.45, 0.64, 0.55, 0.86, 0.00, 0.16]])
    ]
    return data


if __name__ == '__main__':
    N = 9
    theta = radar_factory(N, frame='polygon')

    data = example_data()
    spoke_labels = data.pop(0)

    fig, axes = plt.subplots(figsize=(9, 9), nrows=2, ncols=2,
                             subplot_kw=dict(projection='radar'))
    fig.subplots_adjust(wspace=0.25, hspace=0.20, top=0.85, bottom=0.05)

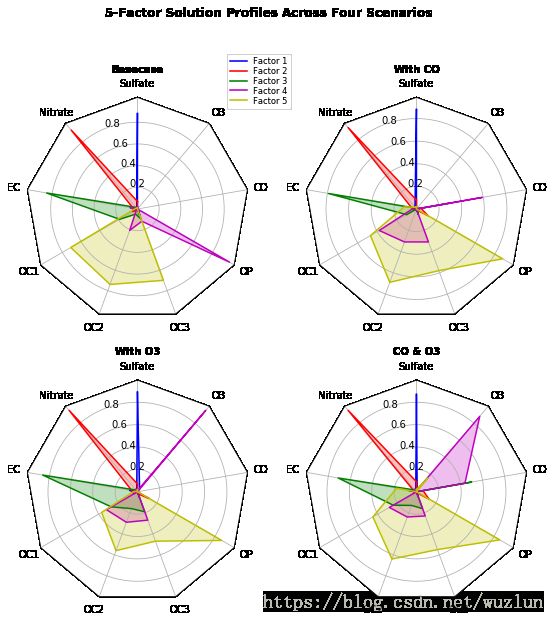
    colors = ['b', 'r', 'g', 'm', 'y']
    # Plot the four cases from the example data on separate axes
    for ax, (title, case_data) in zip(axes.flatten(), data):
        ax.set_rgrids([0.2, 0.4, 0.6, 0.8])
        ax.set_title(title, weight='bold', size='medium', position=(0.5, 1.1),
                     horizontalalignment='center', verticalalignment='center')
        for d, color in zip(case_data, colors):
            ax.plot(theta, d, color=color)
            ax.fill(theta, d, facecolor=color, alpha=0.25)
        ax.set_varlabels(spoke_labels)

    # add legend relative to top-left plot
    ax = axes[0, 0]
    labels = ('Factor 1', 'Factor 2', 'Factor 3', 'Factor 4', 'Factor 5')
    legend = ax.legend(labels, loc=(0.9, .95),
                       labelspacing=0.1, fontsize='small')

    fig.text(0.5, 0.965, '5-Factor Solution Profiles Across Four Scenarios',
             horizontalalignment='center', color='black', weight='bold',
             size='large')

    plt.show()

其它

Matplotlib Logos

%matplotlib inline

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.cm as cm

mpl.rcParams['xtick.labelsize'] = 10
mpl.rcParams['ytick.labelsize'] = 12
mpl.rcParams['axes.edgecolor'] = 'gray'


axalpha = 0.05
figcolor = 'white'
dpi = 80
fig = plt.figure(figsize=(6, 1.1), dpi=dpi)
fig.patch.set_edgecolor(figcolor)
fig.patch.set_facecolor(figcolor)


# 绘制背景
def add_math_background():
    ax = fig.add_axes([0., 0., 1., 1.])

    text = []
    text.append(
        (r"$W^{3\beta}_{\delta_1 \rho_1 \sigma_2} = "
         r"U^{3\beta}_{\delta_1 \rho_1} + \frac{1}{8 \pi 2}"
         r"\int^{\alpha_2}_{\alpha_2} d \alpha^\prime_2 "
         r"\left[\frac{ U^{2\beta}_{\delta_1 \rho_1} - "
         r"\alpha^\prime_2U^{1\beta}_{\rho_1 \sigma_2} "
         r"}{U^{0\beta}_{\rho_1 \sigma_2}}\right]$", (0.7, 0.2), 20))
    text.append((r"$\frac{d\rho}{d t} + \rho \vec{v}\cdot\nabla\vec{v} "
                 r"= -\nabla p + \mu\nabla^2 \vec{v} + \rho \vec{g}$",
                 (0.35, 0.9), 20))
    text.append((r"$\int_{-\infty}^\infty e^{-x^2}dx=\sqrt{\pi}$",
                 (0.15, 0.3), 25))
    text.append((r"$F_G = G\frac{m_1m_2}{r^2}$",
                 (0.85, 0.7), 30))
    for eq, (x, y), size in text:
        ax.text(x, y, eq, ha='center', va='center', color="#11557c",
                alpha=0.25, transform=ax.transAxes, fontsize=size)
    ax.set_axis_off()
    return ax

# 文字
def add_matplotlib_text(ax):
    ax.text(0.95, 0.5, 'matplotlib', color='#11557c', fontsize=65,
            ha='right', va='center', alpha=1.0, transform=ax.transAxes)


# 前面的圆
def add_polar_bar():
    ax = fig.add_axes([0.025, 0.075, 0.2, 0.85], projection='polar')

    ax.patch.set_alpha(axalpha)
    ax.set_axisbelow(True)
    N = 7
    arc = 2. * np.pi
    theta = np.arange(0.0, arc, arc/N)
    radii = 10 * np.array([0.2, 0.6, 0.8, 0.7, 0.4, 0.5, 0.8])
    width = np.pi / 4 * np.array([0.4, 0.4, 0.6, 0.8, 0.2, 0.5, 0.3])
    bars = ax.bar(theta, radii, width=width, bottom=0.0)
    for r, bar in zip(radii, bars):
        bar.set_facecolor(cm.jet(r/10.))
        bar.set_alpha(0.6)

    ax.tick_params(labelbottom=False, labeltop=False,
                   labelleft=False, labelright=False)

    ax.grid(lw=0.8, alpha=0.9, ls='-', color='0.5')

    ax.set_yticks(np.arange(1, 9, 2))
    ax.set_rmax(9)


if __name__ == '__main__':
    main_axes = add_math_background()
    add_polar_bar()
    add_matplotlib_text(main_axes)
    plt.show()

# 贝塞尔曲线
import matplotlib.path as mpath
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt

Path = mpath.Path

fig, ax = plt.subplots()
pp1 = mpatches.PathPatch(
    Path([(0, 0), (1, 0), (1, 1), (0, 0)],
         [Path.MOVETO, Path.CURVE3, Path.CURVE3, Path.CLOSEPOLY]),
    fc="none", transform=ax.transData)

ax.add_patch(pp1)
ax.plot([0.75], [0.25], "ro")
ax.set_title('The red point should be on the path')

plt.show()