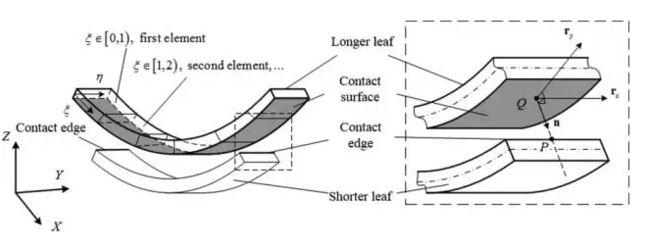
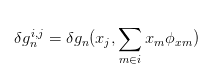接触仿真分析的基本原理是什么?

转自：http://www.featech.com.cn/news/detail/id/170.html

论计算力学里面最技术繁复最拉拉杂杂的项目，要数接触分析。这个领域违反了有限元连续插值的本质，所以要花大量的技巧来解决几何问题并翻译成有限元问题。不幸的是，工业界接触问题无处不在。光是汽车工业的碰撞分析，滚动分析，铸造分析，零件组装分析，都是以解决接触问题为核心。从本文开始，有限元科技小编来花几篇文章聊聊接触分析的基本原理。

除了到求解的阶段会有高数预警，其他时候接触问题的原理其实都很粗暴，而且这组文章性质仅仅是原理介绍，所以我尽量用文字和图形说话。

这篇文章我们先说说接触检测（contactdetection）。

这个应该算是接触技术繁复特点的浓缩。为什么？因为把接触这个现实中很直观的现象要离散化实在是很坑爹的事情。在有限元的范畴下，接触检测的最终目的是生成接触单元，而后者是传递接触边界条件的媒介。（在其他方法如离散元的范畴下，接触检测更多是通过全域搜索实现，而不是局部生成接触单元）。接触检测分两大类，一类是允许穿透，一类是通过检测域不允许穿透。允许穿透是经典的思路，其原理是后知后觉：等单元节点空间位置进入另一个单元，或者单元节点作用力突然增大的时候，程序认为两者搞在一起了。现代算法更多的是应用检测域的思路：slave节点靠近master足够近的时候，不等穿透master就说表过来。所以本质上两类方法区别无非是在小三进门后还是进门前两口子翻脸。因为现在大家都比较警觉，所以我们主要说严防进门的方法。

确定检测域的大小是门艺术，一般软件都有个选择让用户指定检测距离。这样做的问题是，距离定小了影响收敛，定大了那就变成万磁王。所以一般自动设定会以接触面单元尺寸和接触面曲率为参考。以Node-2-Surface接触为例，当slave节点进入检测域，程序就认为这些节点上会发生接触。

下一步就是找到对应的master接触面。最流行的办法是做投影。对某一slave节点(上图节点x)，我们找到master上和该节点距离最近的单元面。所有这些单元面加在一起就是master接触面。问题是，这样的投影不是所有时候都找得到(下图)，或者找到了投影但不唯一。单身问题总比一夫多妻问题严峻，所以有大量研究花在如何处理找不到对应Master接触面的盲点的问题上。处理手段大致有两种，一种是把潜在的master面平滑化（比如贝塞尔曲线和曲面），使单元投影面变得连续。另一种是扩大搜索域，把master投影面延伸到更远的距离。其实最粗暴也是最流行的办法，就是什么都不做，直接找一个距离slave节点最近的master节点(上图节点与y)，然后用这个节点所在的某一个单元生成接触单元。这个类似于在你哥们的女友的闺蜜圈里面找女朋友。从算法的角度，因为是找最近的节点，所以这个过程应用的是搜索，常用的quicksort,heapsort和octree等在各大软件接触检测里面都有应用。

另一个接触检测的难点和重点，是自接触问题。这个常见于壳结构的失稳分析(下图)。经典的检测域方法在这里的应用困难，是分不清在壳的哪一面发生了接触。解决办法依然很粗暴：要么把检测域尺度减小到薄壳厚度一半以内，要么记录结构变形的历史以跟踪结构表面节点的可能接触面。前者的缺点是影响时间步所以求解步增多，后者的缺点是增加内存使用。

最后一个问题就是在什么时候进行接触检测。这又有两类方法：在加载步开始的时候和在迭代步开始的时候。对于前者，接触检测发生在每个荷载步更新的时候。而后者是在每个荷载步的每个牛顿迭代步都进行。二者区别最明显的自然是工作量：因为接触检测运算耗时，所以后者要比前者慢。后者另一个缺陷是稳定性不足。因为迭代步造成的几何的更新有时候会把上个迭代步检测到的节点又归到检测域以外去，造成死循环。基于迭代步的检测的最大优点是精确性高。现代接触软件两种方法都有应用。

知道了程序如何侦测接触的发生，现在就是要让程序形成离散化的接触力学控制方程，所以这里我们来看控制方程的组成。为了简单起见，我们只考虑没有摩擦和粘连的情况。

上次已经说了，接触问题是一个对人类很直观但是对机器很繁琐的问题，其控制方程也不例外。我们知道固体力学基于位移的控制方程无非是下面几坨：

力平衡方程；

位移－应变方程；

本构方程；

边界条件。

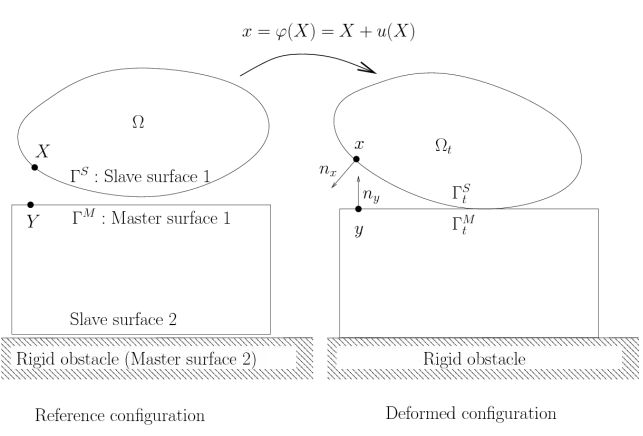
在接触问题上，因为在接触面位移和力边界条件都是未知，所以以上方程我们要稍作修改。以力平衡弱形式为例，考虑接触面之后可以写成：

从左到右各项分别描述了内力，接触应力，边界条件，和体力对力平衡的贡献。因为只考虑无摩擦的情况，接触应力项只包括垂直于接触面的柯西应力分量和垂直于接触面的接触体距离的变分。这是平衡方程中唯一因为接触而添加的项。

针对接触面上的两个新的未知量，数学上有两种途径来应对：

为新的未知量添加新的约束条件。

去掉新的未知量，转而改写以上控制方程的形式。

先来看1：新的约束条件应该只施加于将会（未激活）和已经（已激活）的接触位置上。直观地看，它们大概应该是：

接触体之间的距离不为负数（没有穿透），距离为零表示接触激活；

接触体之间的接触压力不为负数（没有拉扯），压力为零表示接触未激活；

同一个位置，要么接触压力为零（接触没有激活），要么接触距离为零（接触激活）。

这些直观的条件，上个世纪初被人发现是接触问题求解的必要条件。今天通常称为Signorini条件。虽然看似浅显，实际上因为接触问题可以翻译为加上了接触面约束的对内能求变分的约束优化问题，所以Signorini条件等价于优化理论上的KKT条件，身价一下就高大上了。下次你和人家说你知道接触原理，不说你知道Signorini条件都不好打招呼。

根据以上三个约束条件，我们可以得出控制方程中第二项（接触项）恒不为正。把这个结论引入控制方程，我们就实现了上文说的途径2：把控制方程的形式从等式变为了不等式：

所以，我们得到了接触问题的两种表达方式：变分等式方程+Signorini不等式约束，和变分不等式方程。虽然两种描述是等效的，但是因为应用到数值求解还是等式形式更方便，变分不等式除了在理论和定性分析上然并卵。

求解加上了不等式约束的弱形式，优化理论的很多办法都用得上。最流行的是三种：罚函数，拉格朗日乘数，和增强拉格朗日乘数。今天最后就说说罚函数。

罚函数本质上是通过对接触压力形式的规定对Signorini条件提供一种近似。这种近似假设接触面的压力是这么一种函数形式，这个函数满足：

接触体距离大于零的时候函数值为0；

接触发生后，函数值随接触穿透距离而单调增加。

对比一下上文的三个条件，可以发现这样的压力函数和接触体距离关系除了违反“没有穿透”的条件，其他的都满足。为了补偿穿透的条件，罚函数本质上给接触面安了（多）个弹簧，来尽量实现接触体的分离。弹簧的弹性模量由压力函数决定，所以罚函数法的性能直接决定于这个函数的形式。罚函数法是最早应用于接触问题的算法，所以现今所有通用有限元程序都应用了它。所以，下次答辩或者面试，有人问你接触方程罚函数法的原理，请稳稳道出两个词：“Signorini”和"弹簧"。

下次接着说有限元对接触方程的离散。

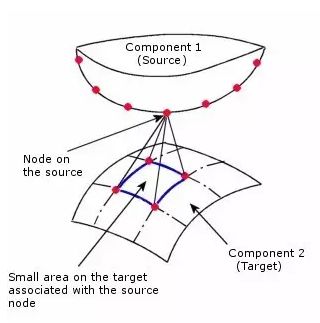
有了接触控制方程，下面就是要进行离散化。这里我们以node-to-surface和罚函数法为例说说接触项的离散。Node-to-surface，顾名思义，两个接触面中，slave面由节点代表，master面由单元面代表。接触检测算法能保证每个slave节点至少对应一个master面，这就是所谓的接触单元。

不像平常我们遇到的结构单元，接触单元是没有实体对应的单元概念，其任务是在离散化的时候负责接触项的离散。换句话说，接触单元的任务是在离散模型中联系两个接触体并传递内力。所以，借用罚函数法的阐释，不妨把接触单元理解为接触体之间的弹簧或者胶水。有趣的是，“胶水”这个比喻恰恰是处理区域分解的Mortar法的意思，而Mortar法在surface-to-surface接触中应用非常多。要注意的是，根据搜索算法和几何构型情况，slave节点可以同时和多个master平面形成接触单元。

在把接触面离散为接触单元后，力平衡方程弱解形式中的接触项就变成了下面这个样子。意思是说，接触面上的虚功由slave节点和master单元面组成的接触单元构成。像上次一样，我们仍然只考虑最简单的没有摩擦的形式。

既然是基于位移的有限元，那么上面这个接触项就应该用位移来表示。所以，最后一步就是把形函数和等参元条件加进来。于是接触压力和接触体距离（gap）的变分表示为

意思是说，在接触单元，接触压力是接触距离的函数（回忆一下罚函数法的弹簧概念）。接触距离是slave节点位置和master单元面表示。而master单元面又是由描述该单元的节点位置和形函数表示。所以这么一来大家都变回了位移－形函数的形式。这也是所有有限元离散的基本思路：控制方程－弱解－形函数表达。

于是至少现在我们在形式上把问题变得和常见有限元形式一致了。后面的就是组成刚度矩阵求解了。因为接触压力的表达形式也含有位移（再回忆下罚函数弹簧），所以通常要求解非线性方程，那于是就交给牛顿法了。

这个系列我们只说了最简单的情形：正面无摩擦接触和罚函数法。把滑动和摩擦加进来之后，问题还要纠结地多。另外，线单元与线单元的接触也有很多技术细节。上面说的方法的还有一个前提：用户事先定义接触体。但在实际应用中，还有很多问题事先是不知道谁和谁会接触的。比如说下图网球击打球拍的问题。动力模拟之前是不知道球体和哪根线单元发生接触的。于是现代求解器都朝着自动解除的傻瓜方向发展，比如说现在ABAQUS已经基本实现了，Ansys，OptiStruct等也在陆续实现。