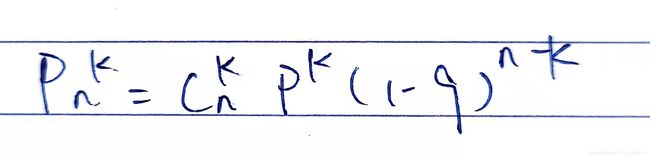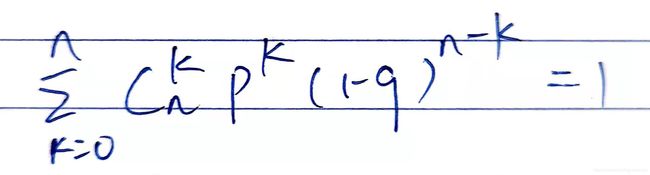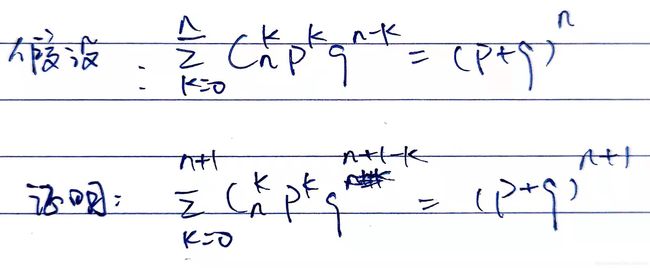【数理统计】神奇的P值

AB Test

工作中经常会通过AB Test帮助做产品决策，简单说就是为产品制作两个（A/B）或多个（A/B/C/...）版本，在同一时间维度，分别让不同组的用户群随机的访问这些版本，收集各群组的用户的数据，最后分析评估出最好版本正式采用。

比如下面的例子，A组看到红色的标题栏，B组看到绿色的标题栏，采集的数据可能每个组有多少比例的用户点击了标题栏。我们希望得到的结果是更多的用户点击，所以B组以37%胜出，最终决定采用绿色的标题栏。

但直接比百分比是不是合理呢？举个简单的例子，A组有10个人看到的界面2个人点击（点击率2/10=20%），B组只有5个人看到2个人点击（点击率2/5=40%），B组就直接以40%胜出吗？显然我们需要更有力的证据说明B的胜出是充分的。这里通常用的方法就是P值。

 

P值和显著性检验

继续上面的例子：A组（control组）：10个人看到2个人点击，点击率0.2；B组（experiment组）：5个人看到2个人点击，点击率0.4。

首先我们先假设B组没有任何作用，或者说，用户根本没有注意到颜色的变化，B的数据完全是在原来的基础上随机得到的。这里，“原来的”也就是20%的概率。也就是说，我们先假设在每个人会有20%概率点击的情况下，计算出现5个人中2个人点击的概率，可以通过二项概率公式计算：

Cn,k表示在n个人中选出2个人的组合数。举个例子，5个人：A，B，C，D，E，出现A，B点击且C，D，E不点击的概率为0.2*0.2*0.8*0.8*0.8=0.2^2*0.8^3，同理出现只有A，C点击的概率也为0.2^2*0.8^3。所以，最终出现5个人中2个人点击的概率为所有情况加起来即C5,2*0.2^2*0.8^3：

所以，在B组没有任何效果的假设下，我们有接近0.2的概率得到5个人中2个人点击的情况。这里求得的0.2048就是P值。

通常，我们选P<0.05的时候拒绝原假设，即认为B组有效果。换句话说，如果P值非常非常小，比如0.0001，即“B组没有任何效果”的假设下只有0.0001的概率会出现B的数据。运用小概率原理：小概率事件在一次实验中几乎不可能发生，我们认为原假设是不合理的，即“B组没有任何效果”的假设是不成立的（B组里一定发成了不同寻常的事情！）。

有点晕的地方可能是怎么用0.4（2/5）？即B组的实际点击率。我的理解是B组首先要通过显著性检验，也就是我们上面的P值检验。如果P值很大，结果“不显著”，那么0.4根本没有任何意义，因为这完全可能是统计误差得到的。只有P值很小的情况下，才认为0.4>0.2的比较是有意义的。

理解P值的计算可以在一定程度上帮助我们理解为什么“不显著”，比如（如果试验真的有效果）通常增加试验样本数是有用的，因为样本小的情况下P值通常很大。极端的例子，如果样本只有1个，那么P值只能是0.2或者0.8，任何结果都“不显著”。再比如上面的例子：5个人中2个人点击是不显著的，但是500个人200个人点击就很显著了。因为在原假设20%概率下出现500个人200点击的概率很小很小。

 

二项概率公式

第一次看到P值的时候，我的点完全集中在了二项概率公式上面。虽然直观的解释很容易理解，但这里隐藏的一个结果就是所有的概率之和为1，即：

验证的了一下，真的为1：

是不是很神奇！好奇宝宝忍不住翻出了当年的数学书：

居然只有一句话带过了，而且自己还留了笔记“用数学归纳法证明”，太“不显然”了！

试着重新证明一遍。所谓归纳法，就是首先n=1的时候是成立，然后假设n的时候成立，尝试证明n+1成立，即：

证明过程如下：

嗯，你可能注意到了，这里有个Cn+1,k的展开：Cn+1,k = Cn,k + Cn,k-1，从排列组合的意义上解释就是，从n+1个人中选k个人的组合数，等于从n个人中选k的组合数（一定不选某个人），加上从n个人中选k-1个人的组合组（一定选了某个人）。如果要证明，也是可以直接推出来的：

看来我的数学还没有完全还给老师！(◍•ᴗ•◍)

 

参考资料

p-value：https://www.baidu.com/link?url=RQaT38MszwZl3ycAsI-Zfl0DAX6htO9u8QkTwLv4drOv6LElHrXFZlu-1fjGbpyn&wd=&eqid=e0e1eccf000ab515000000025d16faeb

《概率论与数理统计》：https://book.douban.com/subject/2256637/