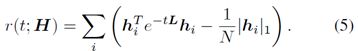论文解读-Multi-scale Anomaly Detection on Attributed Networks

原文：Gutiérrez-Gómez, Leonardo, Bovet A , Delvenne J C . Multi-scale Anomaly Detection on Attributed Networks[J]. 2019.

摘要

当前属性网络在很多领域中得到广泛应用，尤其是社交网络和金融领域，属性网络的边表示实体之间的关系，而实体则由属性网络中的不同节点属性来表示。而异常检测对于发现诸如信用卡欺诈、网络垃圾邮件和网络入侵等异常行为至关生要。属性图中的异常节点是指该节点的属性与参考节点的属性差异较大的节点。当前已经有一部分研究工作对图模型的局部异常、全局异常和社区上下文异常进行了研究，但是由于真实网络的多尺度和节点无数据的异构性，属性图的异常检测依然是一个存在挑战。Here, we propose a principled way to uncover outlier nodes simultaneously with the context with respect to which they are anomalous, at all relevant scales of the network。本文通过评估平滑图中节点的特定信息后节点的浓度来评估节点的异常度。此外，本文还提出了一种用于社区检测的基于图信息处理方式的马尔科夫稳态框架，社区发现主要用于找出异常节点的上下文信息。本文方法在合成数据集和真实数据都进行了验证，表现出优于当前方法的性能。最近本文展示了在大规模图中使用切比雪夫多项式近似的可扩展性。

1引言

异常检测是数据挖掘中的一个非常重要的问题，在不同领域已经进行了大量的研究与应用。例如，信用卡欺诈检测、网络系统入侵检测、通信网络异常用户识别和垃圾邮件检测等等。异常数据可以理解为在模式或行为上严重偏离背景特性的数据。图异常检测研究是一个非常有价值的事情，因是很多系统都可以表示成图模型，属性图就是图中的顶点点带有描述该顶点的，边表示顶点之间的关系。本质上属性不仅仅具有顶点属性，边也具有属性，但是考虑边的属性过于复杂，不做说明的话，这里的属性图通常只表示顶点属性。

例如，在社交网络中，顶点通常表示人，边表示人之间的社会关系，节点属性通常表示人的属性或是统计信息等。在购物网中，顶点表示商品，以及一些用来描述该商品的属性，两个商品之间的关系表示该两件商品被同一个人购买。

由于真实世界网络中的异常产生机制通常是未知的，定义一个具体有效的异常通常是不现实的，因此评估一个节点的异常程度就是一个非常有挑战的工作。

然而，然而，表示复杂的经济、社会或生物系统的真实世界的网络具有模块化、多标量和通常是分层结构的特征，因此，考虑跨网络多尺度结构的节点属性来正确定义异常上下文是至关重要的。此外，异常节点通常是由其上下文决定的，在特定的上下文环境中可能是异常顶点，而在其他上下文中可能就不是异常节点。异常检测与社区发现就很自然的结合到一起。

通过多维度的社区发现算法把相近的节点聚到一类中，以发现异常节点的所有上下文信息，社区发现算法利用顶点属性相似作为顶点之间边的权值来进行计算。在实际情况中一个顶点可能在某个维度属性利群点，但是从全局角度来看就不是了，多维度异常检测方法可以从全局视角发现真正的异常顶点。

图1 工作关系网

图1表示工作关系网。如果一个员工与其他不同部门员工一起工作，而不与自己同部门员工一起工作，那么从办公环境角度来看，该员工有可就是一个异常员式，如图中的Q2。但是如果该员工所在的办公室与他同部门所在的办公室都属性他们部门的话，那么从部门的角度来看该员工又不属于异常员工。从公司的角度来看，公司都是一个大环境，需要从公司的全局视角来进行异常识别。由此可见异常的判别标准依赖于所选择的判断维度，因此异常检测需要从多维度进行评估并结合节点复杂来进行异常检测。

本文的主要贡献如下

1 提出一个新的异常检测算法MADAN。该方法提供一种原则性机制在对属性网络顶点进行异常排序，并在上下文环境中从多维度定位异常点。

2 本方法在合成数据集和真实数据集中进行了验证，结果表示本文提出的访求不仅能找出已确定的异常并进行异常排序，还能从数据集中发现未确定的异常。

3 最后，利用图拉普拉斯指数的切比切夫近似，证明了本文方法的可并行性和可扩展性。此外，该方法还提供了一种利用连续时间Markov稳定框架快更快速的社区检测方法。

相关工作（略）

2算法详解

2.1加权图构建

图的形式化描述，G=（V,E）其中V表示节点集，其中|V|=N表示节点的个数，E表示边集。为了简化描述，本文采用无向、连通的简单图来说明。对于每个节点u∈V ，使用一个d维向量 表示节点的属性，其中 表示节点u的第k个属性。

本文所要解决的问题是在所有可能的上下文范围内找出异常节点以及与之相关的异常上下文。为此，本文中节点之间的边的权值表示顶点的相似度，这里高斯加权函数：

 

（1）

上式中，σ 是一个尺度参数。这基于此创建了加权邻接矩阵，或称为相似矩阵，两个顶点相似，也就是两个顶点的邻节点的属性值相似。这种加权函数在图像处理过程中通常用来表示像素强度之间的相似性。在本文使用高斯加权函数来把节点属性转换成为网络结构。

2.2热核(The heat kernel)

根据邻接矩阵可以定义任意图信号x∈RN ，热方程可以表示为：

D是一个对解矩阵，D的定义如下式：

矩阵L是加权图的拉普拉斯变换。

上面的热方程可用下式求解。

该方程的名字来源于物理领域， 表示节点u的“温度”或“内能”，将在图中基于傅里叶传导定律沿着边按传层率w() 进行传导。更重要的是，动力学保留了信号的平均值。也就可以看成L的每一列的和为0。从物理角度来看，也就是图上的“能量”既不会产生也不会消失，它只会在图中的节点中不断的扩散传播。

在信号处理方面,热内核 往往被视为一个平滑滤波器作用于初始信号x(0)。热内核将x(0)的每一输入替换为其他节点信号的加权平均值(更强调邻近节点)。在参数t的限制下，平滑信号在网络中通常是常数的。

当图是具有固定权值的离散线(例如，建模为离散的一维空间)时，滤波器是平移不变的。这意味着对于任意克罗内克脉冲信号，相应的平滑信息是它自身的平移，因此它们具有相同的形状。如果相应的平滑信息e-tLδu 过于以来u周围网络的结构与权值的话，那这么就损失了平移不变性。这个属性使得使用图内核的特征来描述图的结构特征。并基于些特性检测异常以及异常上下文。

异常节点

图中节点u∈V 在范围t内的浓度可以定义为信号δu 在时刻t的L2范式，表示成如下形式：

（2）

这个度量是有用的，因为过滤器保留了信号的和(或平均值)，因此Kronecker增量的最大范数为1，而完全平滑的信号的范数为1/N，这是分布在N个节点上的和为1的信号的最小可能范数。

在t时刻浓度较高的节点通常只有少数据边或是低权重的边与，因此与其领域的连接性较弱。在t时刻的参考邻节点的范围选择参考以下方法。

通过公式1可发看出，一个高浓度的节点表示该节点的属性与其邻节点属性有很大的不同。通过这种方式，可以使用浓度来量化给定节点在给定时间尺度上相对于其上下文的偏差程度，并为潜在的异常值排序提供评分。

为了识别离群值，本文使用以下标准阈值规则，这些规则在本文的实验中有较好的效果。然而，基于浓度分布也可应用到其他场景中。

使用 表示整体图的浓度，如果节点u在t时刻满足条件：

那么认为u节点在t时刻就是一个异常节点。式中 表示平均浓度， 表示节点的标准差。

现在来了解下t的选择，以及在选择t的情况下与之相关的异常节点的上下文。在一个较大的参数t的限制下，当热核有时间将所有节点的信号混合在一起时，delta信息δu 将在整个图上被平滑到一个常数。因此，对于整个图而言，作为t的离群点的节点就是全局的离群点。相反，一个小的t只允许与直接相邻节点进行热扩散，因此一个小的t离群值与其上下文有明显的不同。

通常如果一个节点集与网络中其他节点有相对较弱的关联，那么认为该节点集是异常节点的上下文，有点类似于社区检测。弱连通的定义是通过衡量在时间尺度t内异常节点上下文中的内能。hs 表示S的特征信号 ，也就是在S内的节点为1，不在的为0。S节点集的初始能量表示为|h_s |1 ，也就是集合S内的节点数量。在平滑后，S中的能量剩余：

目标是最大化该函数。

为了能够找到潜在节点的上下文，需要实现对节点的划分。把图编码成一个NXK的特征矩阵H，其中N表示特征集个数据。其中关于H的最优划分为最大化：

这本质上是马尔可夫稳定性的一个特例，用于设计一个通用的多维度社区检测框架。该框架为较小的t实现一个小节点集的细粒度划分，对于一个大t实现大规模节点集的细粒度划分的预期。由于某些节点可能会被分配到它们自己的独立上下文，为了避免这种情况，在实践中，需要将它们与最近的节点连接起来。

公式5的最大化问题是一个NP-hard问题，对于每一步，使用不同的随机初始化运行Louvain算法100次，并使用公式5作为评分函数对分区H进行排序。为了评估检索分区在给定时间尺度下的鲁棒性，我们采用方法Delvenne et al. 2013计算给定时间内找到的分区集合之间的信息变化。分区P1和P2的信息归一化为：

其中， 是P1关于P2的条件熵。

同时为了找出给定分区之间的相关性，

本文提出的MADAN算法如果上图所示，首先扫描网络以找到最相关的范围和上下文，通过上下文化查找方法找到确定的时间参数t,同时利用公式3检测异常节点。