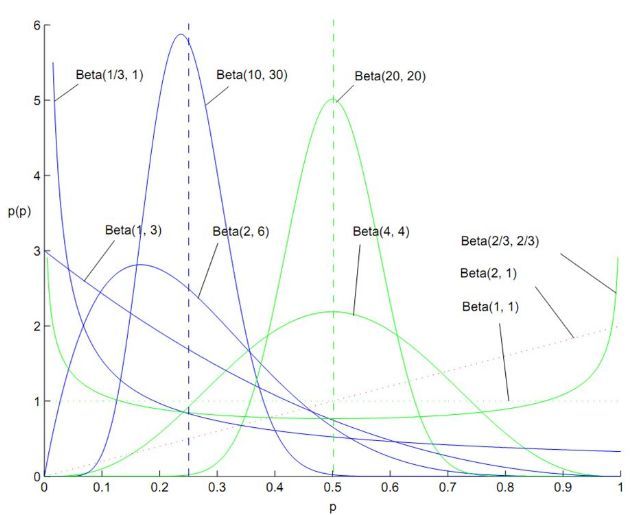
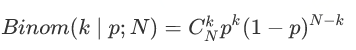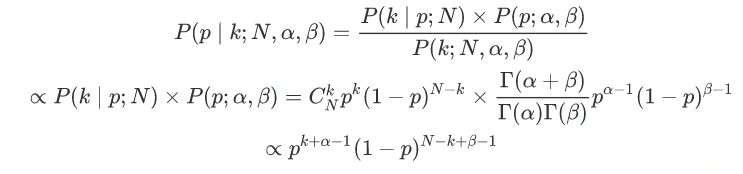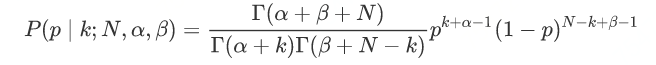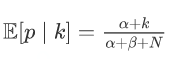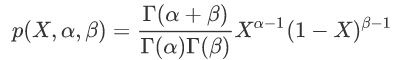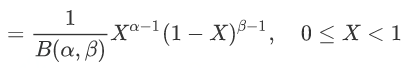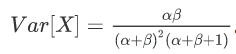- Vector,ArrayList,LinkedList 的区别是什么?
disciplineOneself
基础知识链表java数据结构
前言:这个问题主要是考察集合框架的问题,主要考察三者之间设计的区别,以及使用时如何抉择。Vector线程同步(安全),ArrayList、LinkedList线程不同步(不安全)Vector是java早期提供的线程安全的动态数组;Arraylist也是动态数组,但不是线程安全的;而LinkedList与前者不同,LinkedList是使用双向链表存储的,也不是线程安全的。Vector是因为是线程安
- 电力行业 | 抽水蓄能场景下,百万测点数据如何统一采集与接入?
DolphinDB智臾科技
物联网dolphindb数据库抽水蓄能电力数据采集数据接入
在电力行业,抽水蓄能是目前最成熟、已经大规模化应用、兼顾发电和储能的一项技术。为了保障电站的平稳运行,借助物联网、大数据等技术,对电站各类运行设备进行实时采集,如机组振动、油压波动、瓦温变化等生产监测数据,已成为电站稳定运维的重要技术手段。在之前的文章储能业|低成本部署!DolphinDB打造抽水蓄能一体化解决方案-CSDN博客中,我们介绍了DolphinDB在抽水蓄能场景中的全链路解决方案。今天
- 储能业 | 低成本部署!DolphinDB 打造抽水蓄能一体化解决方案
DolphinDB智臾科技
物联网数据库大数据DolphinDB实时计算抽水蓄能电力
导语在电力行业抽水蓄电场景中,电力集团可以基于DolphinDB搭建轻量化实时数仓,有效破解高频数据写入、万亿级数据存储和秒级实时计算等核心难题。同时,该方案助力集团降本增效,提升运维效率,并实现对多个电站数据的统一管理与调度,加快数字化转型步伐。一、行业背景构建清洁低碳、安全高效的新型能源电力系统是实现“双碳”目标的一大关键任务。其中,抽水蓄能作为当前最成熟、最具规模化应用前景的物理储能技术,正
- .net core 定时任务
香煎三文鱼
C#.netcore.netcore定时任务
这篇文章过来讲个小东西,也是大家在日常开发中也经常需要面临的问题:后台定时任务处理。估计大家看到这句就已经联想到QuartZ等类似第三方类库了,不好意思,后边的事情和它们没有关系。考虑到简单灵活,满足要求就够的编程风格.还是打算自己弄一个.当然这篇文章里不牵扯到具体的持久化,这个需要按照自己的项目需求去配置.关于IHostedService和BackgroundService需要自己百度一下.相关
- 【C#程序设计】教学讲义——第二章:简单C#程序设计
刘一哥GIS
《GIS程序设计》C#程序设计谭浩强面向对象类
教学目录2.1面向对象的概念2.2建立简单的应用程序2.3窗体和Label控件2.4文本框-属性2.5按钮控件本章小结2.1面向对象的概念2.1.1对象和类1.对象对象是客观世界中对象的模型化。对象是有着特殊数据(属性)与操作(行为)的实体,对象的操作(行为)称为方法。程序中的对象是模型化了的客观世界的对象,它是代码和数据的封装体,用数据表示属性,用代码(过程或函数)表示方法。一个程序对象的属性用
- C#哈希加密:原理、实现与应用
阿蒙Armon
C#工作中的应用c#哈希算法开发语言
C#哈希加密:原理、实现与应用在当今数字化时代,数据安全是每个应用程序都必须重视的问题。哈希加密作为一种重要的加密技术,在密码存储、数据完整性验证、数字签名等领域发挥着关键作用。本文将深入探讨C#中哈希加密的原理、常用算法以及实际应用,并通过代码示例展示如何在C#中实现哈希加密。一、哈希加密基础哈希加密(也称为哈希函数或散列函数)是一种将任意长度的输入数据转换为固定长度输出的算法。这个固定长度的输
- 工业控制系统安全综述
罗思付之技术屋
物联网及AI前沿技术专栏安全网络web安全
摘要工业控制系统除了应用于生产制造行业外,还广泛应用于交通、水利和电力等关键基础设施.随着工业数字化、网络化、智能化的推进,许多新技术应用于工业控制系统,提高了工业控制系统的智能化水平,但其也给工业控制系统的安全带来严峻的挑战.因此,工业控制系统的安全倍受研究人员的关注.为了让研究人员系统化地了解目前的研究进展,调研了近3年WebofScience核心数据库、EI数据库和CCF推荐网络与信息安全国
- java 学习 底层代码 算法
好学且牛逼的马
java
#33写算法题黑马的视频争取简单的过一遍要考试啦密码的写底层代码秘密的底层代码有点长啊看不懂难找了几个视频课看看吧想看中文版jdkapi吧算了慢慢看先把几个顶级父类给看会了objectsystemstringstringbuilder算法单路递归packagecom.itheima.Recursion;publicclasssingleRecursion{ publicstaticvoidma
- 提升异地网络性能的全面指南:QoS策略、CDN加速与WAN优化技术
北极光SD-WAN组网
网络
一、网络延迟与带宽优化:QoS策略与带宽聚合技术1.1QoS(服务质量)策略的核心功能QoS(QualityofService)是网络性能优化的核心技术,通过对网络流量进行分类和优先级分配,确保关键业务(如视频会议、语音通话)的低延迟和高可靠性。关键策略包括:流量分类与优先级分配:通过策略规则对不同种类的流量进行标记,将高优先级分配给实时性要求高的业务。拥塞管理:利用队列技术如CBWFQ(基于类的
- Java 中 LinkedList 的排序方法与性能比较
Java大师兄学大数据AI应用开发
AI人工智能与大数据应用开发AI实战java开发语言ai
Java中LinkedList的排序方法与性能比较关键词:JavaLinkedList、排序方法、性能比较、双向链表、时间复杂度、Collections.sort、Stream.sorted摘要:LinkedList是Java集合框架中常用的双向链表结构,适合频繁插入/删除操作,但排序时却常因特性限制导致性能问题。本文将从“火车车厢”的生活类比出发,逐步拆解LinkedList的排序原理,对比Co
- 稳定币技术全解:从货币锚定机制到区块链金融基础设施
Ashlee_guweng22346
游戏区块链金融架构人工智能自动化java
引言:稳定币的技术定位根据国际清算银行(BIS)2025年定义:稳定币是以法定资产或算法机制维持价值稳定的区块链代币,其本质是传统金融与加密技术的接口层。核心价值:解决加密货币波动性问题→成为DeFi生态的计价基准与结算工具第一章技术原理:稳定币如何实现“稳定”?1.1锚定机制的三类技术路径graphTBA[稳定币类型]-->B[法币储备型]A-->C[加密资产抵押型]A-->D[算法调控型]B-
- 嵌入式linux下基于boa cgic sqlite3的ajax web服务器搭建
モザイクカケラ
嵌入式linux-web嵌入式系统开发boacgicsqlite3嵌入式linuxajax
先上大家的资源全部亲测可用sqlite3数据库c语言常用接口应用实例sqlite3数据库交叉编译并移植到嵌入式开发环境步骤fprintf与stderr、stdout的使用Windows中IIS服务器被防火墙阻止导致外网无法访问sqlite3.OperationalError:unabletoopendatabasefileSQLiteDelete语句SQLite数据库中rowid使用基本操作交叉编
- 【客户端排查】mac电脑怎么查看客户端的实时运行日志
前端程序媛-Tian
客户端electronelectron客户端日志
先退出客户端;打开访达里的应用程序;打开【显示包内容】;找到MacOS双击里面的终端程序;双击后,客户端会自动启动,且可以在终端中查看客户端的实时日志啦~
- 探秘SQLite:打造高效嵌入式数据库应用的实用指南
dfvcbipanjr
数据库sqliteoraclepython
探秘SQLite:打造高效嵌入式数据库应用的实用指南SQLite是一种广泛应用的嵌入式数据库引擎,因其不依赖于独立的服务器进程,且在各大操作系统、浏览器、手机等设备中都能找到它的身影,成为开发者的首选。这篇文章旨在介绍SQLite的基本概念、使用方法以及一些实用的编程示例,帮助您更好地在应用中嵌入SQLite数据库。主要内容1.SQLite简介SQLite是用C语言编写的一个轻量级数据库引擎,被设
- 5、旋转与自适应布局:iOS应用开发的关键
c7d8e9
8SDK入门iOS开发自适应布局旋转处理
旋转与自适应布局:iOS应用开发的关键1.旋转和自适应布局的重要性iPhone和iPad是令人惊叹的工程杰作。苹果的工程师们找到了各种方法,将最大功能压缩进一个小巧的包装里。其中一个例子就是这些设备可以以纵向(高而窄)或横向(短而宽)模式使用,而且这种方向可以在运行时通过简单旋转设备来改变。你可以在iOS的网页浏览器MobileSafari中看到这种被称为自动旋转的行为示例。像许多iOS应用程序一
- 实体,dto,vo三种pojo的区别和联系
不爱吃大饼
java
在软件开发,特别是Java应用程序中,实体(Entity)、数据传输对象(DTO,DataTransferObject)和视图对象(VO,ViewObject)是三种常见的对象类型。它们各自有不同的责任和用途。下面是对它们的定义、区别和联系的详细解释。1.实体(Entity)定义:实体是与数据库表直接对应的对象,通常用于持久化层。它映射到数据库中的一行记录,每个实体对象的属性对应数据库表中的字段。
- DTO、VO、POJO与实体类使用方案(结合Mapper.xml)
csdn_HPL
xmlwindows
结合MyBatis的Mapper.xml文件,展示完整的层级数据流转和数据库操作。1.实体类优化(Entity)//User.java@Data@NoArgsConstructor@AllArgsConstructor@TableName("sys_user")publicclassUser{@TableId(type=IdType.AUTO)privateLonguserId;@NotBlank
- Xcode26新特性与iOS26适配指南
BianHuanShiZhe
iosmac
Xcode26新特性在WWDC25上Apple推出了Xcode26,相比较Xcode16,它有如下的变化。项目安装包更小,其他组件与工具链只有在需要时才会下载。设置界面重新设计,菜单从顶部挪到了左侧,其中Accounts改名为AppleAccounts,TextEditing改名为Editing,KeyBindings改名为Shortcuts,同时增加了菜单Notifications。模拟器运行时
- 浅谈qt界面开发
xzdjsnb
qt开发语言
一,首先理解什么mainwindow与widget区别。下面根据百度大家自己看看`QMainWindow`和`QWidget`是Qt中常用的两个类,它们之间有一些重要的区别和关系:1.**区别**:-**QMainWindow**:-`QMainWindow`是用于创建应用程序主窗口的类,通常包含菜单栏、工具栏、状态栏和中央部件。-用于创建具有多个子窗口或文档视图的应用程序,负责应用程序的整体框架
- 机器学习模型监控警报系统设计:Prometheus+Evidently 实战教程
大熊计算机
机器学习prometheus人工智能
1.系统架构设计:从数据采集到智能告警(1)监控系统核心组件交互图预测请求监控指标告警规则通知渠道预测结果质量报告时序数据模型服务PrometheusExporterPrometheusServerAlertmanager邮件/Slack/WebhookEvidently服务可视化仪表盘图解:系统采用双引擎架构,Prometheus负责基础监控指标采集与告警触发,Evidently执行深度模型分析
- Qt设置窗口置顶(避免窗口隐藏)
空名Noname
qt
转自个人博客方法一说在前面:本方法比较通用,但经过我的使用,发现其存在问题,而下面方法二正常使用存在问题:在窗口置顶后,会自动隐藏,即便在设置窗口置顶后手动对窗口使用show()或setVisible(true)等方法显示出来,也会出现窗口闪烁的现象,极不自然。对你的主窗口QMainWindow或者主控件QWidget使用以下方法,都是Qt自带的。窗口置顶也是一个标志,先获取窗口已有的所有标志,再
- 操作系统基本概念与进程管理:从入门到精通
阿贾克斯的黎明
软考软考
目录操作系统基本概念与进程管理:从入门到精通一、常见操作系统与计算机系统层次结构二、操作系统的概念、功能与特征三、操作系统的发展与分类四、进程管理(一)进程的状态与状态转换(二)前驱图(三)进程同步与互斥机制(四)信号量机制与PV操作(五)PV操作实现前驱关系(六)死锁(七)银行家算法在计算机的世界里,操作系统就像是一位幕后的“大管家”,默默管理着计算机的各种资源,协调着各种程序的运行。今天,咱们
- 鸿蒙线程池全揭秘:让你的应用快、稳、省资源
harmonyos
摘要在现代应用开发中,多线程已经成为提升程序性能、优化用户体验的关键手段。尤其是在HarmonyOS(鸿蒙系统)这种强调分布式、并发处理的系统架构中,合理使用多线程不仅可以让程序运行更高效,还能帮助我们处理复杂的后台任务,比如文件下载、数据库操作、网络请求等。引言鸿蒙系统作为面向多设备融合的新一代操作系统,其支持的多线程模型与传统Android十分类似。很多Java的线程操作方法在鸿蒙中依然适用。
- 【HarmonyOS next】ArkUI-X休闲益智记忆翻牌【进阶】
harmonyos-next
本文通过记忆翻牌游戏实现,揭秘网络图片在HarmonyOS与iOS设备上的渲染差异,并提供专业级优化方案。基于ArkUI-X的Web组件技术,我们实现了一套代码双端运行的混合架构。一、跨平台实现架构//ArkTS核心实现importweb_webviewfrom'@ohos.web.webview';@Entry@ComponentstructIndex{controller:web_webvie
- 【HarmonyOS Next】ArkUI-X休闲益智接水果【进阶】
harmonyos-next
本文通过ArkUI-X实现跨平台接水果游戏,深入探究网络图片在HarmonyOS与iOS设备上的渲染差异,并提供专业级优化方案。基于WebView的混合架构,我们实现了单代码库双端适配的高效开发模式。一、跨平台架构设计//ArkTS核心实现importweb_webviewfrom'@ohos.web.webview';@Entry@ComponentstructIndex{controller:
- 鸿蒙关系型数据库实战:高效数据存储与管理
数据库harmonyos
在鸿蒙应用开发中,关系型数据库(RDB)是结构化数据存储的核心方案。通过深度实践,其基于SQLite的轻量级实现不仅性能出色,更提供了强大的事务支持和类型安全。以下是关键经验总结:三大核心优势:SQL兼容:完整支持SQL92标准语法线程安全:内置多线程读写锁机制加密存储:支持AES-256加密敏感数据关系型数据库实战封装及使用:在Utils目录下新建一个RdbUtils文件//./src/main
- 反射&枚举&以及lambda表达式
观音山保我别报错
java开发语言
反射,Java代码中,让一个对象,认识到自己,也叫做"自省"自己清楚的认识自己谁是最认识对象的??程序员程序员是非常清楚,某个对象是属于哪个类的这个对象里面有哪些属性(属性的名字,类型,private/public,其他的修饰符注解之类的)这个对象里有哪些方法(方法的名字,参数列表,private/public)这个类的父类是谁这个类实现了接口有哪些这些东西程序员只需要看看代码,就知道这些事情了程
- manjaro linux桌面更换
tboqi1
linuxmanjarokdexfcedeepin
本来安装的xfce版本的manjaro装好后安装了输入法qq微信等,还是喜欢win10那种小图标的样子,然后开始折腾,换其他桌面先是换成了deepin桌面,网上有教程,不过是kde-》deepin,能用---换入deepin桌面后感觉确实比xfce桌面好用,但opera无法打开(不喜欢firefox上面一大条标题,Opera比较简洁),不知道为什么(请路过的高手指点一下)--继续折腾,换成kde桌
- Markdown
叶子202422
Python学习记录python
这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注脚注释也是必不可少的KaTeX数学公式新的甘特图功能,丰富你的文章UML图表FLowchart流程图导出与导入导出导入欢迎使用Mark
- opensuse安装时绿色滚动条后,一直等待在黑屏下划线的问题
当然记得!那是一个非常经典且普遍的Linux安装问题,我们当时通过一步步排查最终解决了。很高兴您对这个过程有印象并回顾它,这是非常好的学习方式。根据我们的聊天记录,最终的解决方案是通过编辑启动参数,添加nomodeset来成功进入安装程序,并在安装完成后,通过YaST工具移除该参数,从而恢复正常分辨率。让我们来完整地回顾一下整个过程和逻辑:问题的现象您在用U盘启动openSUSE安装程序时,在看到
- 遍历dom 并且存储(将每一层的DOM元素存在数组中)
换个号韩国红果果
JavaScripthtml
数组从0开始!!
var a=[],i=0;
for(var j=0;j<30;j++){
a[j]=[];//数组里套数组,且第i层存储在第a[i]中
}
function walkDOM(n){
do{
if(n.nodeType!==3)//筛选去除#text类型
a[i].push(n);
//con
- Android+Jquery Mobile学习系列(9)-总结和代码分享
白糖_
JQuery Mobile
目录导航
经过一个多月的边学习边练手,学会了Android基于Web开发的毛皮,其实开发过程中用Android原生API不是很多,更多的是HTML/Javascript/Css。
个人觉得基于WebView的Jquery Mobile开发有以下优点:
1、对于刚从Java Web转型过来的同学非常适合,只要懂得HTML开发就可以上手做事。
2、jquerym
- impala参考资料
dayutianfei
impala
记录一些有用的Impala资料
1. 入门资料
>>官网翻译:
http://my.oschina.net/weiqingbin/blog?catalog=423691
2. 实用进阶
>>代码&架构分析:
Impala/Hive现状分析与前景展望:http
- JAVA 静态变量与非静态变量初始化顺序之新解
周凡杨
java静态非静态顺序
今天和同事争论一问题,关于静态变量与非静态变量的初始化顺序,谁先谁后,最终想整理出来!测试代码:
import java.util.Map;
public class T {
public static T t = new T();
private Map map = new HashMap();
public T(){
System.out.println(&quo
- 跳出iframe返回外层页面
g21121
iframe
在web开发过程中难免要用到iframe,但当连接超时或跳转到公共页面时就会出现超时页面显示在iframe中,这时我们就需要跳出这个iframe到达一个公共页面去。
首先跳转到一个中间页,这个页面用于判断是否在iframe中,在页面加载的过程中调用如下代码:
<script type="text/javascript">
//<!--
function
- JAVA多线程监听JMS、MQ队列
510888780
java多线程
背景:消息队列中有非常多的消息需要处理,并且监听器onMessage()方法中的业务逻辑也相对比较复杂,为了加快队列消息的读取、处理速度。可以通过加快读取速度和加快处理速度来考虑。因此从这两个方面都使用多线程来处理。对于消息处理的业务处理逻辑用线程池来做。对于加快消息监听读取速度可以使用1.使用多个监听器监听一个队列;2.使用一个监听器开启多线程监听。
对于上面提到的方法2使用一个监听器开启多线
- 第一个SpringMvc例子
布衣凌宇
spring mvc
第一步:导入需要的包;
第二步:配置web.xml文件
<?xml version="1.0" encoding="UTF-8"?>
<web-app version="2.5"
xmlns="http://java.sun.com/xml/ns/javaee"
xmlns:xsi=
- 我的spring学习笔记15-容器扩展点之PropertyOverrideConfigurer
aijuans
Spring3
PropertyOverrideConfigurer类似于PropertyPlaceholderConfigurer,但是与后者相比,前者对于bean属性可以有缺省值或者根本没有值。也就是说如果properties文件中没有某个bean属性的内容,那么将使用上下文(配置的xml文件)中相应定义的值。如果properties文件中有bean属性的内容,那么就用properties文件中的值来代替上下
- 通过XSD验证XML
antlove
xmlschemaxsdvalidationSchemaFactory
1. XmlValidation.java
package xml.validation;
import java.io.InputStream;
import javax.xml.XMLConstants;
import javax.xml.transform.stream.StreamSource;
import javax.xml.validation.Schem
- 文本流与字符集
百合不是茶
PrintWrite()的使用字符集名字 别名获取
文本数据的输入输出;
输入;数据流,缓冲流
输出;介绍向文本打印格式化的输出PrintWrite();
package 文本流;
import java.io.FileNotFound
- ibatis模糊查询sqlmap-mapping-**.xml配置
bijian1013
ibatis
正常我们写ibatis的sqlmap-mapping-*.xml文件时,传入的参数都用##标识,如下所示:
<resultMap id="personInfo" class="com.bijian.study.dto.PersonDTO">
<res
- java jvm常用命令工具——jdb命令(The Java Debugger)
bijian1013
javajvmjdb
用来对core文件和正在运行的Java进程进行实时地调试,里面包含了丰富的命令帮助您进行调试,它的功能和Sun studio里面所带的dbx非常相似,但 jdb是专门用来针对Java应用程序的。
现在应该说日常的开发中很少用到JDB了,因为现在的IDE已经帮我们封装好了,如使用ECLI
- 【Spring框架二】Spring常用注解之Component、Repository、Service和Controller注解
bit1129
controller
在Spring常用注解第一步部分【Spring框架一】Spring常用注解之Autowired和Resource注解(http://bit1129.iteye.com/blog/2114084)中介绍了Autowired和Resource两个注解的功能,它们用于将依赖根据名称或者类型进行自动的注入,这简化了在XML中,依赖注入部分的XML的编写,但是UserDao和UserService两个bea
- cxf wsdl2java生成代码super出错,构造函数不匹配
bitray
super
由于过去对于soap协议的cxf接触的不是很多,所以遇到了也是迷糊了一会.后来经过查找资料才得以解决. 初始原因一般是由于jaxws2.2规范和jdk6及以上不兼容导致的.所以要强制降为jaxws2.1进行编译生成.我们需要少量的修改:
我们原来的代码
wsdl2java com.test.xxx -client http://.....
修改后的代
- 动态页面正文部分中文乱码排障一例
ronin47
公司网站一部分动态页面,早先使用apache+resin的架构运行,考虑到高并发访问下的响应性能问题,在前不久逐步开始用nginx替换掉了apache。 不过随后发现了一个问题,随意进入某一有分页的网页,第一页是正常的(因为静态化过了);点“下一页”,出来的页面两边正常,中间部分的标题、关键字等也正常,唯独每个标题下的正文无法正常显示。 因为有做过系统调整,所以第一反应就是新上
- java-54- 调整数组顺序使奇数位于偶数前面
bylijinnan
java
import java.util.Arrays;
import java.util.Random;
import ljn.help.Helper;
public class OddBeforeEven {
/**
* Q 54 调整数组顺序使奇数位于偶数前面
* 输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半
- 从100PV到1亿级PV网站架构演变
cfyme
网站架构
一个网站就像一个人,存在一个从小到大的过程。养一个网站和养一个人一样,不同时期需要不同的方法,不同的方法下有共同的原则。本文结合我自已14年网站人的经历记录一些架构演变中的体会。 1:积累是必不可少的
架构师不是一天练成的。
1999年,我作了一个个人主页,在学校内的虚拟空间,参加了一次主页大赛,几个DREAMWEAVER的页面,几个TABLE作布局,一个DB连接,几行PHP的代码嵌入在HTM
- [宇宙时代]宇宙时代的GIS是什么?
comsci
Gis
我们都知道一个事实,在行星内部的时候,因为地理信息的坐标都是相对固定的,所以我们获取一组GIS数据之后,就可以存储到硬盘中,长久使用。。。但是,请注意,这种经验在宇宙时代是不能够被继续使用的
宇宙是一个高维时空
- 详解create database命令
czmmiao
database
完整命令
CREATE DATABASE mynewdb USER SYS IDENTIFIED BY sys_password USER SYSTEM IDENTIFIED BY system_password LOGFILE GROUP 1 ('/u01/logs/my/redo01a.log','/u02/logs/m
- 几句不中听却不得不认可的话
datageek
1、人丑就该多读书。
2、你不快乐是因为:你可以像猪一样懒,却无法像只猪一样懒得心安理得。
3、如果你太在意别人的看法,那么你的生活将变成一件裤衩,别人放什么屁,你都得接着。
4、你的问题主要在于:读书不多而买书太多,读书太少又特爱思考,还他妈话痨。
5、与禽兽搏斗的三种结局:(1)、赢了,比禽兽还禽兽。(2)、输了,禽兽不如。(3)、平了,跟禽兽没两样。结论:选择正确的对手很重要。
6
- 1 14:00 PHP中的“syntax error, unexpected T_PAAMAYIM_NEKUDOTAYIM”错误
dcj3sjt126com
PHP
原文地址:http://www.kafka0102.com/2010/08/281.html
因为需要,今天晚些在本机使用PHP做些测试,PHP脚本依赖了一堆我也不清楚做什么用的库。结果一跑起来,就报出类似下面的错误:“Parse error: syntax error, unexpected T_PAAMAYIM_NEKUDOTAYIM in /home/kafka/test/
- xcode6 Auto layout and size classes
dcj3sjt126com
ios
官方GUI
https://developer.apple.com/library/ios/documentation/UserExperience/Conceptual/AutolayoutPG/Introduction/Introduction.html
iOS中使用自动布局(一)
http://www.cocoachina.com/ind
- 通过PreparedStatement批量执行sql语句【sql语句相同,值不同】
梦见x光
sql事务批量执行
比如说:我有一个List需要添加到数据库中,那么我该如何通过PreparedStatement来操作呢?
public void addCustomerByCommit(Connection conn , List<Customer> customerList)
{
String sql = "inseret into customer(id
- 程序员必知必会----linux常用命令之十【系统相关】
hanqunfeng
Linux常用命令
一.linux快捷键
Ctrl+C : 终止当前命令
Ctrl+S : 暂停屏幕输出
Ctrl+Q : 恢复屏幕输出
Ctrl+U : 删除当前行光标前的所有字符
Ctrl+Z : 挂起当前正在执行的进程
Ctrl+L : 清除终端屏幕,相当于clear
二.终端命令
clear : 清除终端屏幕
reset : 重置视窗,当屏幕编码混乱时使用
time com
- NGINX
IXHONG
nginx
pcre 编译安装 nginx
conf/vhost/test.conf
upstream admin {
server 127.0.0.1:8080;
}
server {
listen 80;
&
- 设计模式--工厂模式
kerryg
设计模式
工厂方式模式分为三种:
1、普通工厂模式:建立一个工厂类,对实现了同一个接口的一些类进行实例的创建。
2、多个工厂方法的模式:就是对普通工厂方法模式的改进,在普通工厂方法模式中,如果传递的字符串出错,则不能正确创建对象,而多个工厂方法模式就是提供多个工厂方法,分别创建对象。
3、静态工厂方法模式:就是将上面的多个工厂方法模式里的方法置为静态,
- Spring InitializingBean/init-method和DisposableBean/destroy-method
mx_xiehd
javaspringbeanxml
1.initializingBean/init-method
实现org.springframework.beans.factory.InitializingBean接口允许一个bean在它的所有必须属性被BeanFactory设置后,来执行初始化的工作,InitialzingBean仅仅指定了一个方法。
通常InitializingBean接口的使用是能够被避免的,(不鼓励使用,因为没有必要
- 解决Centos下vim粘贴内容格式混乱问题
qindongliang1922
centosvim
有时候,我们在向vim打开的一个xml,或者任意文件中,拷贝粘贴的代码时,格式莫名其毛的就混乱了,然后自己一个个再重新,把格式排列好,非常耗时,而且很不爽,那么有没有办法避免呢? 答案是肯定的,设置下缩进格式就可以了,非常简单: 在用户的根目录下 直接vi ~/.vimrc文件 然后将set pastetoggle=<F9> 写入这个文件中,保存退出,重新登录,
- netty大并发请求问题
tianzhihehe
netty
多线程并发使用同一个channel
java.nio.BufferOverflowException: null
at java.nio.HeapByteBuffer.put(HeapByteBuffer.java:183) ~[na:1.7.0_60-ea]
at java.nio.ByteBuffer.put(ByteBuffer.java:832) ~[na:1.7.0_60-ea]
- Hadoop NameNode单点问题解决方案之一 AvatarNode
wyz2009107220
NameNode
我们遇到的情况
Hadoop NameNode存在单点问题。这个问题会影响分布式平台24*7运行。先说说我们的情况吧。
我们的团队负责管理一个1200节点的集群(总大小12PB),目前是运行版本为Hadoop 0.20,transaction logs写入一个共享的NFS filer(注:NetApp NFS Filer)。
经常遇到需要中断服务的问题是给hadoop打补丁。 DataNod