3500 字算法刷题精华总结
第一周周报完整 pdf 版下载地址:
https://t.zsxq.com/rBMVzbM
第二周周报完整 pdf 下载地址:
https://t.zsxq.com/YJiiQz7
本周第三周周报请于星球内下载
上周星球活跃度官方数据如下,连续三周星球活跃度都很不错,感谢星友们的参与,继续努力+坚持。

Day 18:二分查找算法
Day 17 作业题
写出几种常见复杂度对应的算法,星友们给出的答案都很准确,在这里参考星友聂磊的答案:
时间复杂度:
常见操作:哈希查找,数组取值,常数加减乘除
: 二分查找
计算数组中所有元素和,最大,最小
: 归并排序,堆排序,希尔排序,快速排序
² :冒泡,选择排序
:三元方程暴力求解
:求解所有子集
:全排列问题。比如:给定字母串,每个字母必须使用,且一次组合中只能使用一次,求所有组合方式;另外还要经典的旅行商 TSP 问题
下面这幅图太直观了:
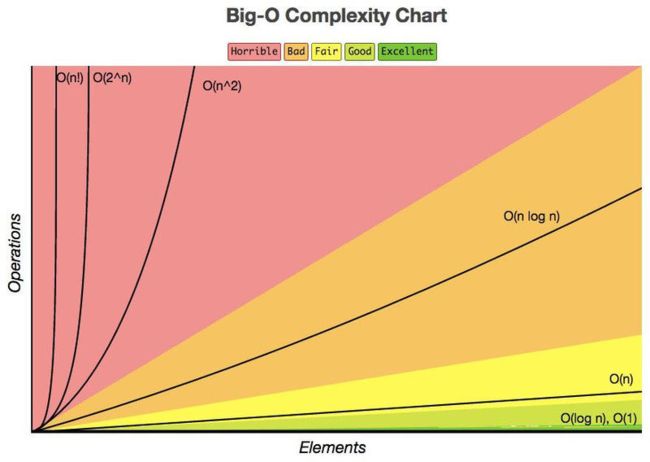
其中,复杂度为: , 是难解的问题, , ² 都是可以接受的解, , 的解是梦寐以求的。
Day 18 :二分查找
二分查找算法,binary search algorithm,也称折半搜索算法、对数搜索算法
它的使用前提:是一种在有序数组中查找某一特定元素的搜索算法。
请补全下面二分查找算法:
# 返回hkey在数组中的索引位置
def binary_search(arr, left, right, hkey):
"""
arr:有序数组
left:查找区间左侧
right:查找区间右侧
hkey:带查找的关键码
备注:left, right 都包括在内,找不到返回 -1
"""
#
#
#
Day 19 合并两个有序序列
Day 18 作业总结
写出二分查找算法
已知函数原型:
def binary_search(arr,left,right,hkey):
pass
要求补全上述代码
注意事项:
(left+right) //2 ,更好写法:left + (right-left)//2
迭代中,一定注意while判断中等号问题
二分查找的代码还是很容易写出bug
迭代二分查找
代码参考星友 Leven:
def binary_search(arr,left,right,hkey):
while left <= right:
mid = left + (right-left) // 2
if arr[mid] == hkey:
return mid
elif arr[mid] > hkey: # 严格大于
right = mid - 1
else: # 此处严格小于
left = mid + 1
return -1 # 表示找不到
if __name__ == "__main__":
sorted_list = [1,2,3,4,5,6,7,8]
result = binary_search(sorted_list,0,7,4)
print(result)
递归二分查找
def binary_search(arr,left,right,hkey):
if len(arr) == 0:
return -1
if left > right:
return -1
mid = left + (right-left) // 2
if arr[mid] == hkey:
return mid
elif arr[mid] < hkey: # 严格小于
return binary_search(arr,mid+1,right,hkey) # 折半
else:
return binary_search(arr,left,mid-1,hkey)
if __name__ == "__main__":
sorted_list = [1,2,3,4,5,6,7,8]
result = binary_search(sorted_list,0,7,4)
print(result)
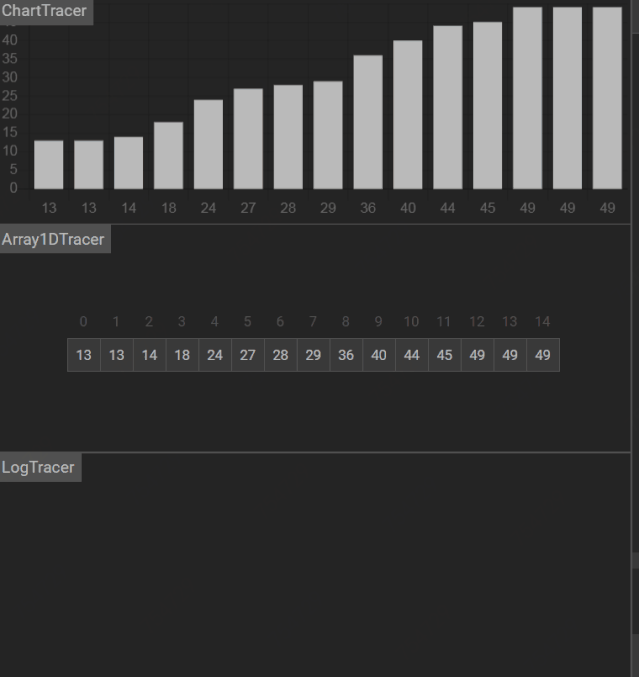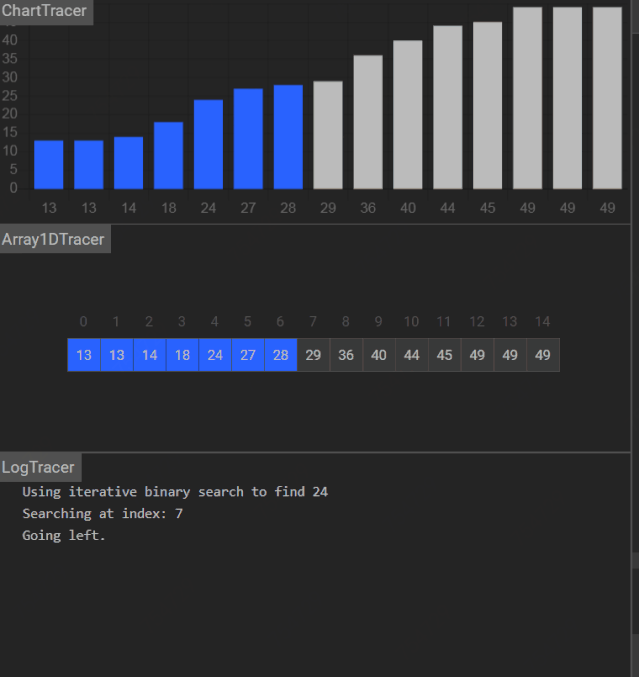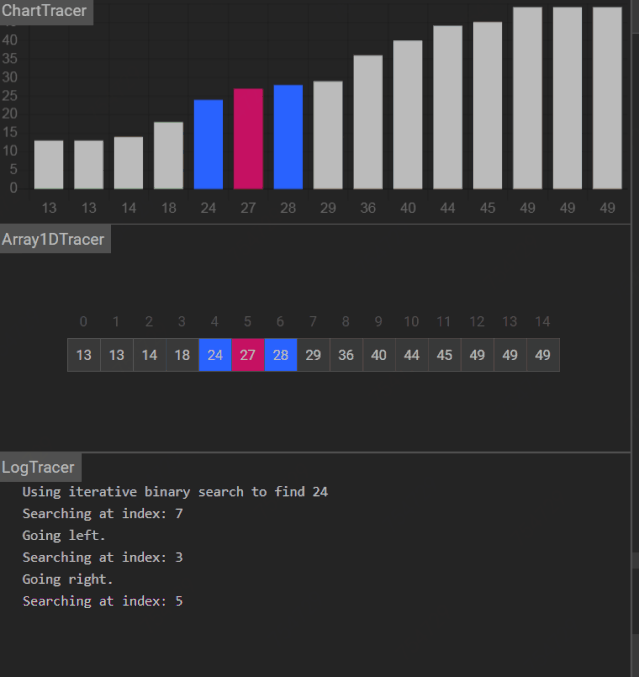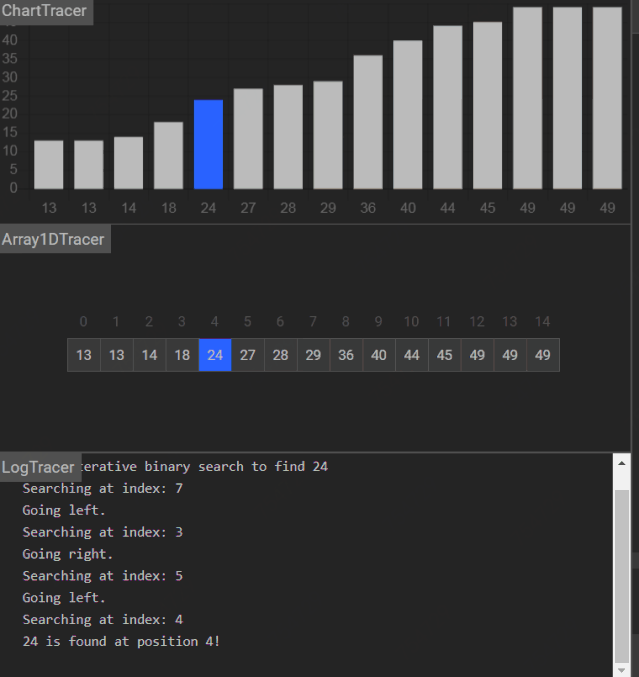
更多演示动画
不能找到关键码:
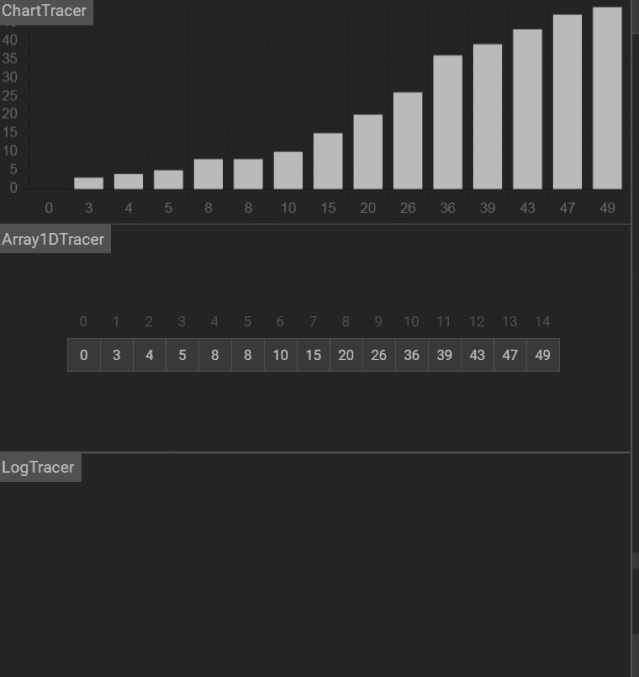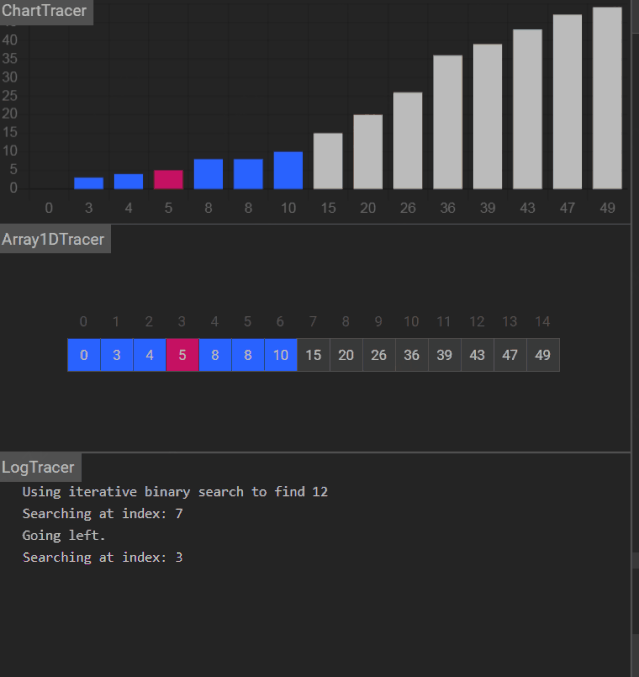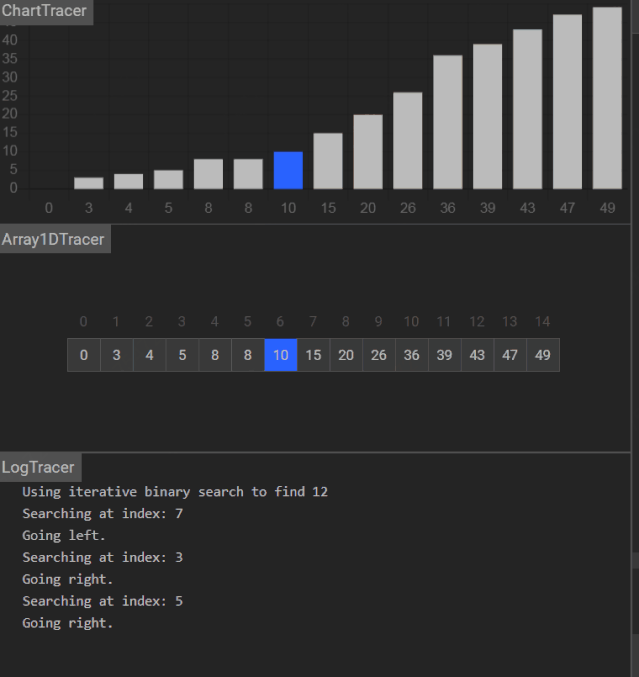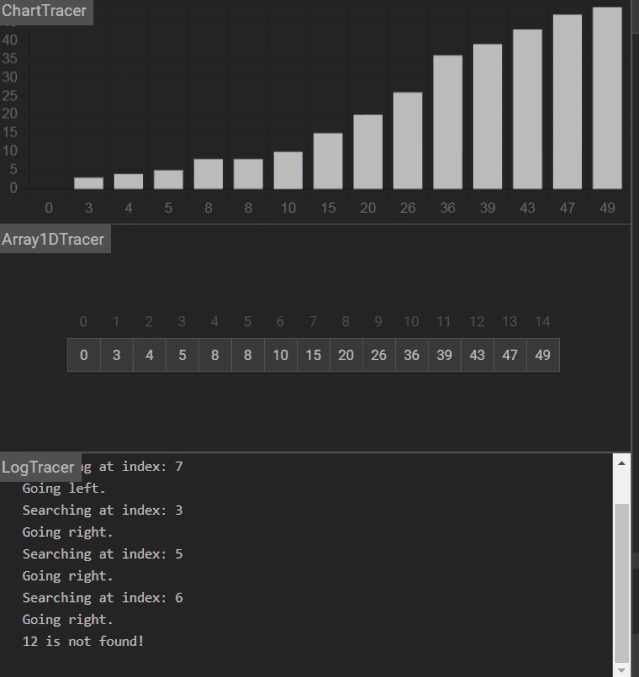
Day 19 作业题
合并两个有序数组 left 和 right:
def merge(left,right):
#补全代码
#
return temp
思路可参考示意图:
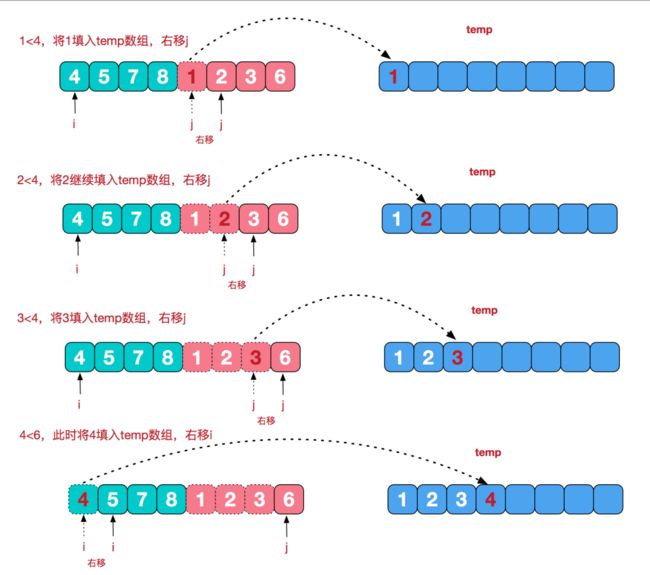
Day 20 归并排序算法
Day 19 合并两个有序数组作业总结
合并两个有序数组
利用两个数组原本已经有序的特点:
def merge(left, right):
i = 0
j = 0
temp = []
while i <= len(left) - 1 and j <= len(right) - 1:
if left[i] <= right[j]:
temp.append(left[i])
i += 1
else:
temp.append(right[j])
j += 1
temp += left[i:] + right[j:]
return temp
print(merge([1,3,4],[2,3,3]))
思路可参考示意图:

Day20 写出归并排序算法
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
归并排序算法的核心正是 Day 19 的合并两个有序数组,补全如下代码:
def merge_sort(lst):
#
#
#
return lst_sorted
归并排序两阶段:
先分,直到长度1,然后再合:
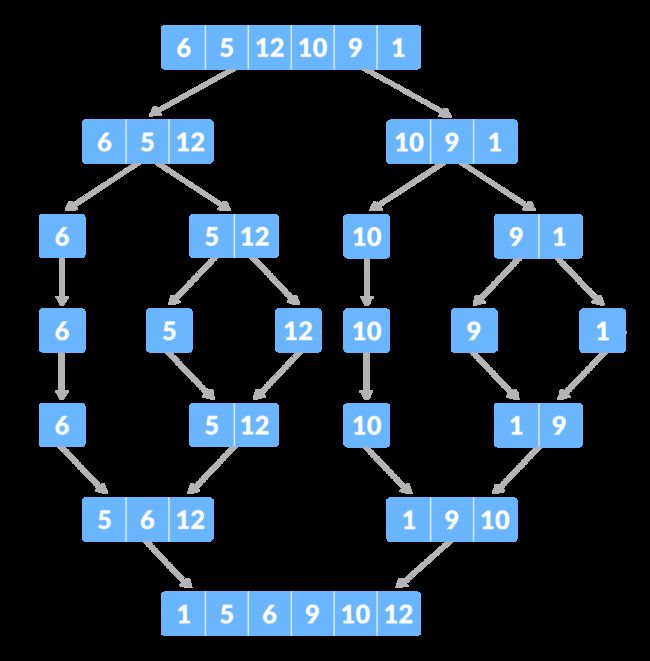
归并排序的详细讲解,可参考:https://www.programiz.com/dsa/merge-sort
Day 21 21 天刷题总结
很多星友都一直坚持到现在,21 天整,都说 21 天养成一个习惯,据此推断,相信你们养成了刷题的习惯~~
下面我们先总结下 Day 20 的归并排序作业题
Day 20 写出归并排序算法
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
# Python program for implementation of MergeSort
def mergeSort(arr):
if len(arr) >1:
mid = len(arr)//2 # Finding the mid of the array
L = arr[:mid] # Dividing the array elements
R = arr[mid:] # into 2 halves
mergeSort(L) # Sorting the first half
mergeSort(R) # Sorting the second half
i = j = k = 0
# Copy data to temp arrays L[] and R[]
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i+= 1
else:
arr[k] = R[j]
j+= 1
k+= 1
# Checking if any element was left
while i < len(L):
arr[k] = L[i]
i+= 1
k+= 1
while j < len(R):
arr[k] = R[j]
j+= 1
k+= 1
验证调用:
# Code to print the list
def printList(arr):
for i in range(len(arr)):
print(arr[i], end =" ")
print()
# driver code to test the above code
if __name__ == '__main__':
arr = [12, 11, 13, 5, 6, 7]
print ("Given array is", end ="\n")
printList(arr)
mergeSort(arr)
print("Sorted array is: ", end ="\n")
printList(arr)
思路可参考示意图:

归并排序的详细讲解,可参考:
https://www.programiz.com/dsa/merge-sort
Day 21 打卡
与这么多星友一起刷题的这21天,请写出你的心得体会,另外若你有什么建议,欢迎也反馈一下。
Day 22 21 天刷题总结
很多星友都一直坚持到现在,21 天整,都说 21 天养成一个习惯,据此推断,相信你们养成了刷题的习惯~~
下面我们看看星友们的刷题心得总结:
Day 21 天刷题总结
节选几位星友21天刷题总结











还有更多星友的21天打卡总结,在此不一一列举。
总之,看到大家有收获,所以与大家一起坚持下去,大的指导方向不变。按照有些星友的反馈,会增加进阶题目,同时周末会增加算法学习经验分享等。
Day 22 打卡:使用递归以相反的顺序打印字符串
前面的归并排序,用到递归。
递归是计算机科学中的一个重要概念。它是计算机算法的基础。接下来几天,我们详细的探讨递归的原理,如何更高效的使用递归解决实际问题。
今天先从一个基础题目体会递归的原理:使用递归以相反的顺序打印字符串。
def reverse_print(s):
#
#补充完整
#
谢谢大家!
Day 23:
Day 22:使用递归以相反的顺序打印字符串
先看题目的求解方法。
递归方法一:
def reverse_print(s):
if len(s) <= 1:
return s
return reverse_print(s[1:]) + s[0]
使用递归,往往代码会很简洁,但若不熟悉递归,理解起来就会相对困难。
下面借助示意图解释以上递归过程:
假如这样调用 reverse_print :
reverse_print('abcdef')
那么递归过程时,函数reverse_print会不断入栈,示意图如下:

此时栈顶为入参 f 的函数,位于示意图的最底部。
因为它满足了递归返回条件len(s) <= 1,所以栈顶函数首先出栈,并返回值 f,下一个即将出栈的为入参ef的函数,其返回值为fe,如下所示:

依次出栈:

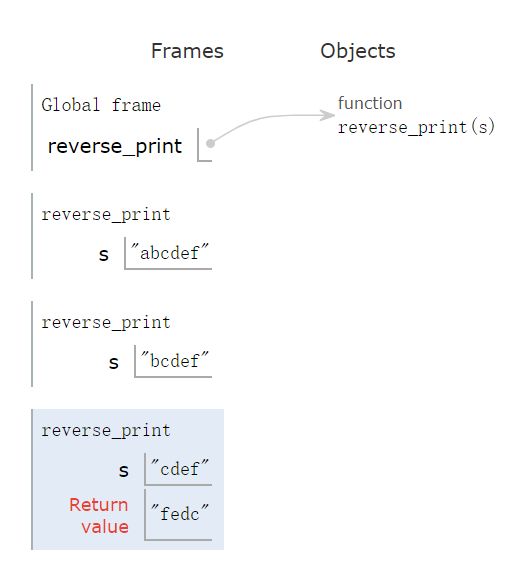
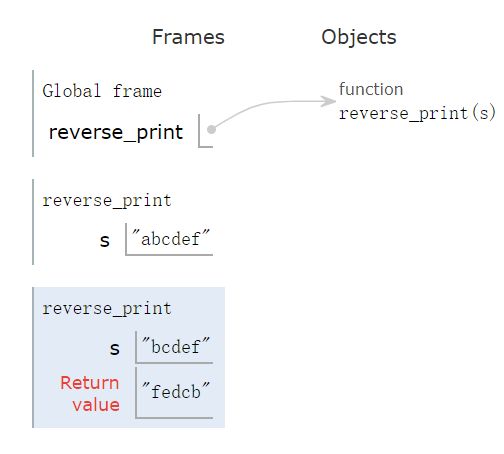
最后一个留在栈的reverse_print,即将返回我们想要的结果: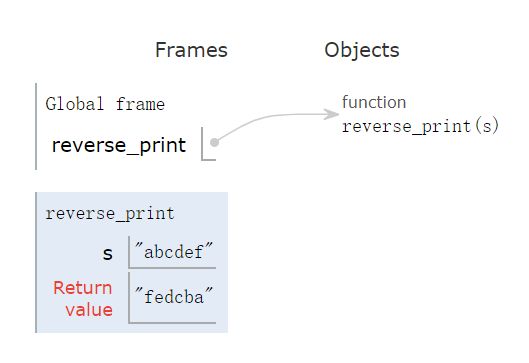
它也出栈后,我们变得到结果 fedcba
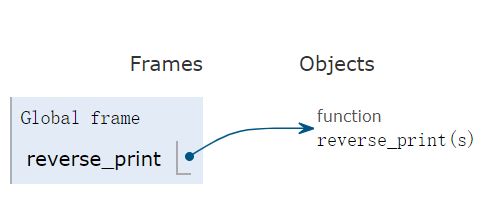
以上就是使用递归反转打印字符的方法。
其他使用递归反转字符串的方法,大家多看看其他星友的解法即可。
Day 23:使用递归:两两交换链表中的节点
给定链表,交换每两个相邻节点并返回其头节点。
例如,对于列表 1-> 2 -> 3 -> 4,我们应当返回新列表 2 -> 1 -> 4 -> 3 的头节点。
请补充下面函数:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def swapPairs(self, head: ListNode):
pass # 请补充
Day 24:递归生成杨辉三角
先来总结昨天的作业
Day 23:递归两两交换链表中的节点
给定链表,交换每两个相邻节点并返回其头节点。
例如,对于列表 1-> 2 -> 3 -> 4,我们应当返回新列表 2 -> 1 -> 4 -> 3 的头节点。
请补充下面函数:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def swapPairs(self, head: ListNode):
pass # 请补充
使用递归的解题思路,见下面示意图:
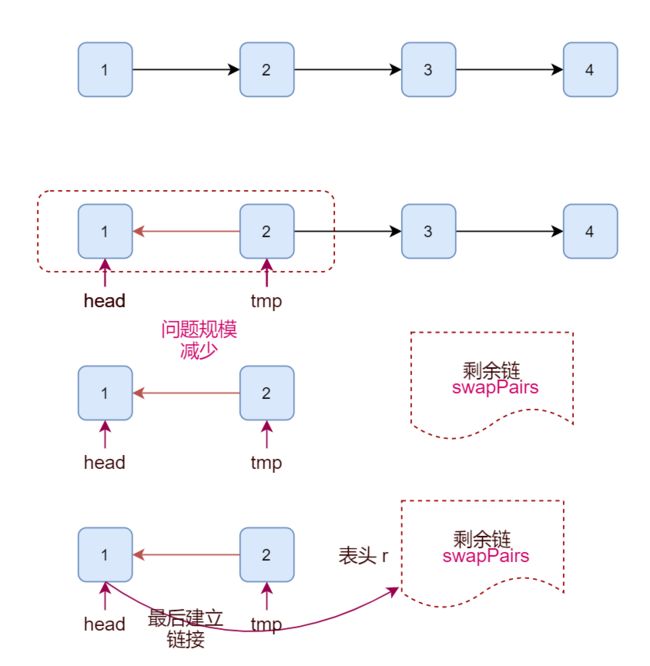
兑现为代码如下:
class Solution:
def swapPairs(self, head: ListNode) -> ListNode:
if head is None or head.next is None:
return head
tmp = head.next
r = self.swapPairs(tmp.next)
tmp.next = head
head.next = r
return tmp
连上完整的验证代码:
# Definition for singly-linked list.
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
class Solution:
def swapPairs(self, head: ListNode) -> ListNode:
if head is None or head.next is None:
return head
tmp = head.next
r = self.swapPairs(tmp.next)
tmp.next = head
head.next = r
return tmp
if __name__ == "__main__":
# create ListNode from list a
a = [1, 2, 3, 4, 5]
head = ListNode(a[0])
tmp = head
for i in range(1, len(a)):
node = ListNode(a[i])
tmp.next = node
tmp = tmp.next
# swap pairs
snode = Solution().swapPairs(head)
# check result
tmp = snode
while tmp:
print(tmp.val)
tmp = tmp.next
递归使用的诀窍:
每当递归函数调用自身时,它都会将给定的问题拆解为子问题。递归调用继续进行,直到到子问题无需进一步递归就可以解决的地步。
刚刚接触递归,使用起来会比较别扭,大家不妨结合昨天的递归调用栈,再多练习几道递归题目,相信会越来越熟练。
Day 24:递归生成杨辉三角
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
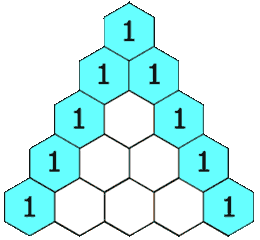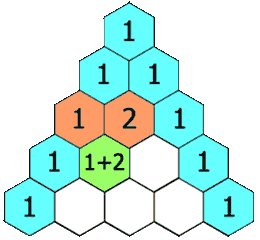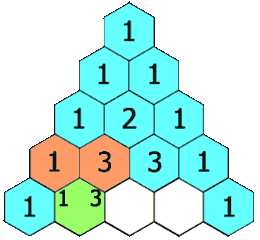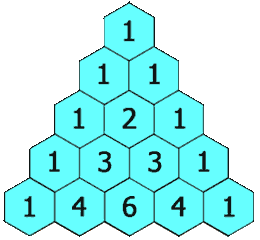
请补全下面代码:
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
pass
如果你想从零学习算法,不妨加入下面星球,现在是最划算的时候,还提供专门的星友微信交流社群,每天在星球里记录自己的学习过程,学习其他星友的解题分析思路。打卡 300 天退换除平台收取的其他所有费用。
若有帮助,点个在看