神经网络-误差反向传播算法(一)
图解深度学习笔记
误差反向传播算法
误差反向传播算法通过比较实际输出和期望输出得到误差信号,把误差信号从输出层逐层向前传播得到各层的误差信号,再通过调整各层的连接权重以减小误差。权重的调整主要使用梯度下降法。
本文主要为以下方面的推导
- 单层感知器
- 不含中间层的多层感知器
- 包含中间层的多层感知器
- 有多个输出函数的多层感知器
一、单层感知器
期望输出 r r r和网络的实际输出 y y y计算最小二乘误差函数 E E E
连接权重 w w w 、 η \eta η 表学习率 、 sigmoid \text{sigmoid} sigmoid函数作为激活函数 f ( u ) f(u) f(u)
单层感知器: ∂ E ∂ w i = ∂ E ∂ y ∂ y ∂ w i ( 1 ) \frac{\partial E}{\partial w_{i}}=\frac{\partial E}{\partial y} \frac{\partial y}{\partial w_{i}} \qquad(1) ∂wi∂E=∂y∂E∂wi∂y(1)设 y = f ( u ) y=f(u) y=f(u) ,求误差函数 E E E对 w i w_i wi的导数: ∂ E ∂ w i = − ( r − y ) ∂ y ∂ w i = − ( r − y ) ∂ f ( u ) ∂ w i ( 2 ) \frac{\partial E}{\partial w_{i}}=-(r-y) \frac{\partial y}{\partial w_{i}}=-(r-y) \frac{\partial f(u)}{\partial w_{i}} \qquad(2) ∂wi∂E=−(r−y)∂wi∂y=−(r−y)∂wi∂f(u)(2) f ( u ) f(u) f(u)的导数就是对复合函数求导 ∂ E ∂ w i = − ( r − y ) ∂ f ( u ) ∂ u ∂ u ∂ w i ( 3 ) \frac{\partial E}{\partial w_{i}}=-(r-y) \frac{\partial f(u)}{\partial u} \frac{\partial u}{\partial w_{i}} \qquad(3) ∂wi∂E=−(r−y)∂u∂f(u)∂wi∂u(3) u u u对 w i w_i wi求导的结果只和 x i x_i xi相关 ∂ u ∂ w i = x i ( 4 ) \frac{\partial u}{\partial w_{i}}=x_{i} \qquad(4) ∂wi∂u=xi(4)
将公式 ( 4 ) (4) (4)代入 ( 3 ) (3) (3)公式,得到下式 ∂ E ∂ w i = − ( r − y ) x i ∂ f ( u ) ∂ u ( 5 ) \frac{\partial E}{\partial w_{i}}=-(r-y) x_{i} \frac{\partial f(u)}{\partial u} \qquad(5) ∂wi∂E=−(r−y)xi∂u∂f(u)(5)对 sigmoid \text{sigmoid} sigmoid函数求导 ∂ f ( u ) ∂ u = f ( u ) ( 1 − f ( u ) ) ( 6 ) \frac{\partial f(u)}{\partial u}=f(u)(1-f(u)) \qquad(6) ∂u∂f(u)=f(u)(1−f(u))(6)将公式 ( 6 ) (6) (6)代入 ( 5 ) (5) (5)公式,得到下式 ∂ E ∂ w i = − ( r − y ) x i f ( u ) ( 1 − f ( u ) ) ( 7 ) \frac{\partial E}{\partial w_{i}}=-(r-y) x_{i} f(u)(1-f(u)) \qquad(7) ∂wi∂E=−(r−y)xif(u)(1−f(u))(7)由于 y = f ( u ) y=f(u) y=f(u),可以计算出单层感知器的权重调整值: Δ w i = − η ∂ E ∂ w i = η ( r − y ) y ( 1 − y ) x i ( 8 ) \Delta w_{i}=-\eta \frac{\partial E}{\partial w_{i}}=\eta(r-y) y(1-y) x_{i} \qquad(8) Δwi=−η∂wi∂E=η(r−y)y(1−y)xi(8)
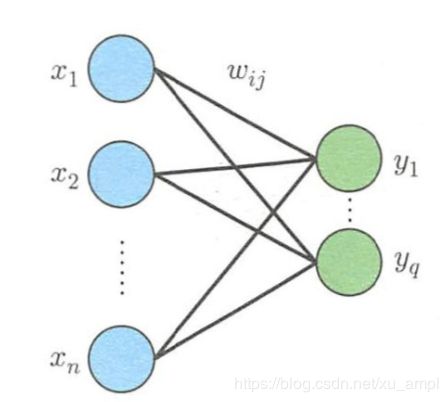
二、不含中间层的多层感知器
不含中间层的感知器误差函数 E E E等于各输出单元的误差总和 E = 1 2 ∑ j = 1 q ( r j − y j ) 2 ( 9 ) E=\frac{1}{2} \sum_{j=1}^{q}\left(r_{j}-y_{j}\right)^{2} \qquad(9) E=21j=1∑q(rj−yj)2(9)对误差函数求导 ∂ E ∂ w i j = ∂ E ∂ y j ∂ y j ∂ w i j ( 10 ) \frac{\partial E}{\partial w_{i j}}=\frac{\partial E}{\partial y_{j}} \frac{\partial y_{j}}{\partial w_{i j}} \qquad(10) ∂wij∂E=∂yj∂E∂wij∂yj(10) w i j w_{ij} wij表示 x i x_i xi和 y i y_i yi之间的权重,对 E E E求导的结果只和 y i y_i yi相关,如下所示: ∂ E ∂ w i j = − ( r j − y j ) ∂ y j ∂ w i j ( 11 ) \frac{\partial E}{\partial w_{i j}}=-\left(r_{j}-y_{j}\right) \frac{\partial y_{j}}{\partial w_{i j}} \qquad(11) ∂wij∂E=−(rj−yj)∂wij∂yj(11)复合函数求导 ∂ E ∂ w i j = − ( r j − y j ) ∂ y j ∂ u j ∂ u j ∂ w i j ( 12 ) \frac{\partial E}{\partial w_{i j}}=-\left(r_{j}-y_{j}\right) \frac{\partial y_{j}}{\partial u_{j}} \frac{\partial u_{j}}{\partial w_{i j}} \qquad(12) ∂wij∂E=−(rj−yj)∂uj∂yj∂wij∂uj(12)和单层感知器一样,对误差函数求导 ∂ E ∂ w i j = − ( r j − y j ) y j ( 1 − y j ) x i ( 13 ) \frac{\partial E}{\partial w_{i j}}=-\left(r_{j}-y_{j}\right) y_{j}\left(1-y_{j}\right) x_{i} \qquad(13) ∂wij∂E=−(rj−yj)yj(1−yj)xi(13)权重调整值如下所示 Δ w i j = η ( r j − y j ) y j ( 1 − y j ) x i ( 14 ) \Delta w_{i j}=\eta\left(r_{j}-y_{j}\right) y_{j}\left(1-y_{j}\right) x_{i} \qquad(14) Δwij=η(rj−yj)yj(1−yj)xi(14)
三、包含中间层的多层感知器
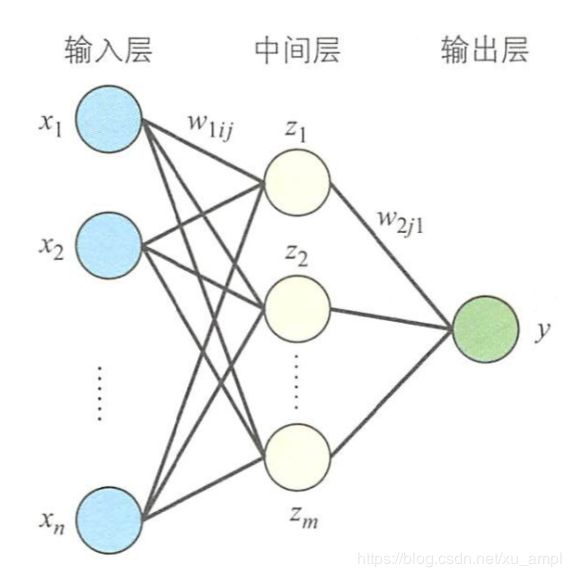
只有一个输出单元 y y y的多层感知器
w 1 i j w_{1 i j} w1ij表示输入层与中间层之间的连接权重, w 2 j 1 w_{2 j 1} w2j1表示中间层和输入层之间的连接权重。 i i i表示输入层单元, j j j表示中间层的单元
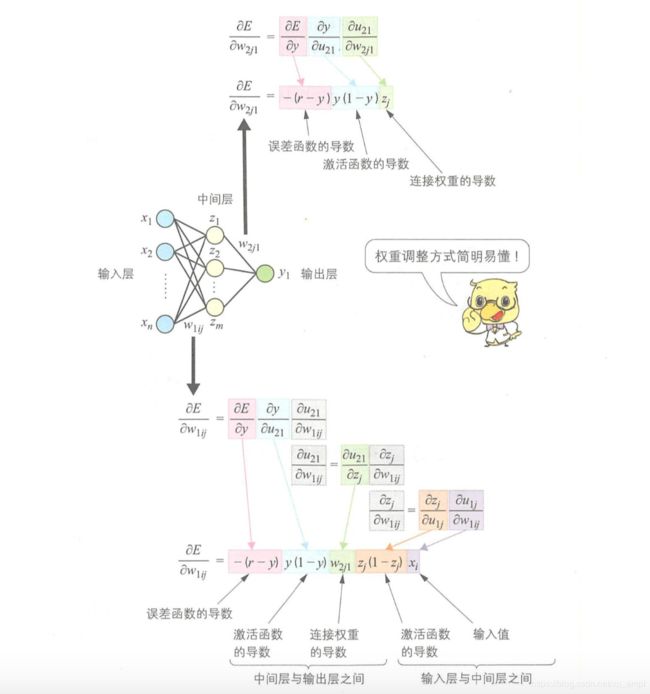
误差函数 E E E对连接权重 w 2 j 1 w_{2 j 1} w2j1求导展开成复合函数求导 ∂ E ∂ w 2 j 1 = ∂ E ∂ y ∂ y ∂ u 21 ∂ u 21 ∂ w 2 j 1 ( 15 ) \frac{\partial E}{\partial w_{2 j 1}}=\frac{\partial E}{\partial y} \frac{\partial y}{\partial u_{21}} \frac{\partial u_{21}}{\partial w_{2 j 1}} \qquad(15) ∂w2j1∂E=∂y∂E∂u21∂y∂w2j1∂u21(15)对误差函数求导 ∂ E ∂ w 2 j 1 = − ( r − y ) y ( 1 − y ) z j ( 16 ) \frac{\partial E}{\partial w_{2 j 1}}=-(r-y) y(1-y) z_{j} \qquad(16) ∂w2j1∂E=−(r−y)y(1−y)zj(16)这里 z j z_j zj表示的是中间层的值。于是,连接权重调整值如下所示: Δ w 2 j 1 = η ( r − y ) y ( 1 − y ) z j ( 17 ) \Delta w_{2 j 1}=\eta(r-y) y(1-y) z_{j} \qquad(17) Δw2j1=η(r−y)y(1−y)zj(17)下面调整输入层与中间层之间的连接权重。输入层与中间层之间的连接权重调整值是根据输出层的误差函数确定的,求导公式如下所示: ∂ E ∂ w 1 i j = ∂ E ∂ y ∂ y ∂ u 21 ∂ u 21 ∂ w 1 i j = − ( r − y ) y ( 1 − y ) ∂ u 21 ∂ w 1 i j ( 18 ) \begin{aligned} \frac{\partial E}{\partial w_{1 i j}} &=\frac{\partial E}{\partial y} \frac{\partial y}{\partial u_{21}} \frac{\partial u_{21}}{\partial w_{1 i j}} \\ &=-(r-y) y(1-y) \frac{\partial u_{21}}{\partial w_{1 i j}} \end{aligned} \qquad(18) ∂w1ij∂E=∂y∂E∂u21∂y∂w1ij∂u21=−(r−y)y(1−y)∂w1ij∂u21(18)与中间层与输出层之间的权重调整值的计算方法相同,输出 y y y也是把公式展开后进行复合函数求导。这里是中间层与输出层单元之间的激活值 u 21 u_{21} u21对输入层与中间层之间的连接权重 w 1 i j w_{1 i j} w1ij求导。 u 21 u_{21} u21由中间层的值 z j z_j zj和连接权重 w 2 j 1 w_{2 j 1} w2j1计算得到。对 z j z_j zj求导可以得到下式 ∂ u 21 ∂ w 1 i j = ∂ u 21 ∂ z j ∂ z j ∂ w 1 i j ( 19 ) \frac{\partial u_{21}}{\partial w_{1 i j}}=\frac{\partial u_{21}}{\partial z_{j}} \frac{\partial z_{j}}{\partial w_{1 i j}} \qquad(19) ∂w1ij∂u21=∂zj∂u21∂w1ij∂zj(19)下式是中间层与输出层单元之间的激活值 u 21 u_{21} u21对中间层的值 z j z_j zj求导,结果只和连接权重 w 2 j 1 w_{2 j 1} w2j1相关 ∂ u 21 ∂ z j = w 2 j 1 ( 20 ) \frac{\partial u_{21}}{\partial z_{j}}=w_{2 j 1} \qquad(20) ∂zj∂u21=w2j1(20)下面是中间层的值 z j z_j zj对连接权重 w 1 i j w_{1 i j} w1ij求导 ∂ z j ∂ w i j = ∂ z j ∂ u 1 j ∂ u 1 j ∂ w 1 i j ( 21 ) \frac{\partial z_{j}}{\partial w_{i j}}=\frac{\partial z_{j}}{\partial u_{1 j}} \frac{\partial u_{1 j}}{\partial w_{1 i j}} \qquad(21) ∂wij∂zj=∂u1j∂zj∂w1ij∂u1j(21)对 z j z_j zj求导 ∂ z j ∂ u 1 j = z j ( 1 − z j ) ( 22 ) \frac{\partial z_{j}}{\partial u_{1 j}}=z_{j}\left(1-z_{j}\right) \qquad(22) ∂u1j∂zj=zj(1−zj)(22)输入层和中间层单元之间的激活值 u 1 j u_{1 j} u1j,对中间层和输出层间的连接权重 w 1 i j w_{1 i j} w1ij求导,结果只和 x i x_i xi有关 ∂ u 1 j ∂ w 1 i j = x i ( 23 ) \frac{\partial u_{1 j}}{\partial w_{1 i j}}=x_{i} \qquad(23) ∂w1ij∂u1j=xi(23)根据公式 ( 20 ) − ( 23 ) (20)-(23) (20)−(23),于是公式 ( 19 ) (19) (19)为如下所示 ∂ u 21 ∂ w 1 i j = w 2 j 1 z j ( 1 − z j ) x i ( 24 ) \frac{\partial u_{21}}{\partial w_{1 i j}}=w_{2 j 1} z_{j}\left(1-z_{j}\right) x_{i} \qquad(24) ∂w1ij∂u21=w2j1zj(1−zj)xi(24)根据公式 ( 18 ) (18) (18)和 ( 24 ) (24) (24),对输入层与中间层之间的连接权重 w 1 i j w_{1 i j} w1ij求导 ∂ E ∂ w 1 i j = − ( r − y ) y ( 1 − y ) w 2 j 1 z j ( 1 − z j ) x i ( 25 ) \frac{\partial E}{\partial w_{1 i j}}=-(r-y) y(1-y) w_{2 j 1} z_{j}\left(1-z_{j}\right) x_{i} \qquad(25) ∂w1ij∂E=−(r−y)y(1−y)w2j1zj(1−zj)xi(25)最后得到的中间层与输出层之间的连接权重调整值如此: Δ w 2 j 1 = η ( r − y ) y ( 1 − y ) z j ( 26 ) \Delta w_{2 j 1}=\eta(r-y) y(1-y) z_{j} \qquad(26) Δw2j1=η(r−y)y(1−y)zj(26)得到的输入层与中间层之间的连接权重调整值如下所示: Δ w 1 i j = η ( r − y ) y ( 1 − y ) w 2 j 1 z j ( 1 − z j ) x i ( 27 ) \Delta w_{1 i j}=\eta(r-y) y(1-y) w_{2 j 1} z_{j}\left(1-z_{j}\right) x_{i} \qquad(27) Δw1ij=η(r−y)y(1−y)w2j1zj(1−zj)xi(27)上述步骤汇总的结果如下图所示:
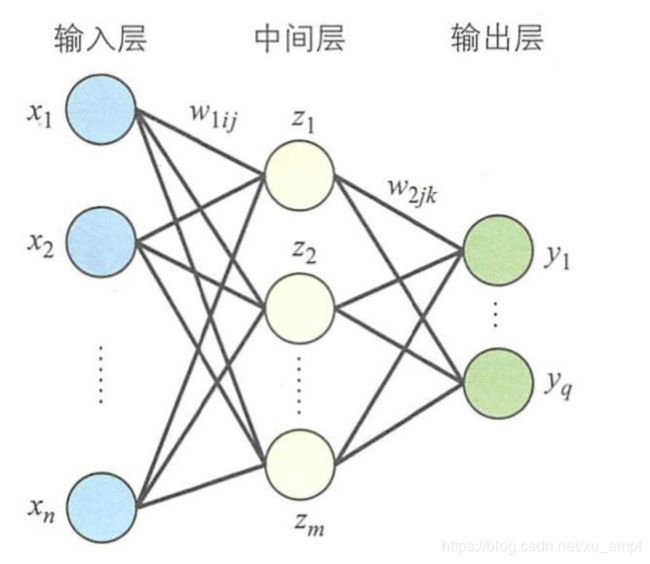
四、有多个输出函数的多层感知器
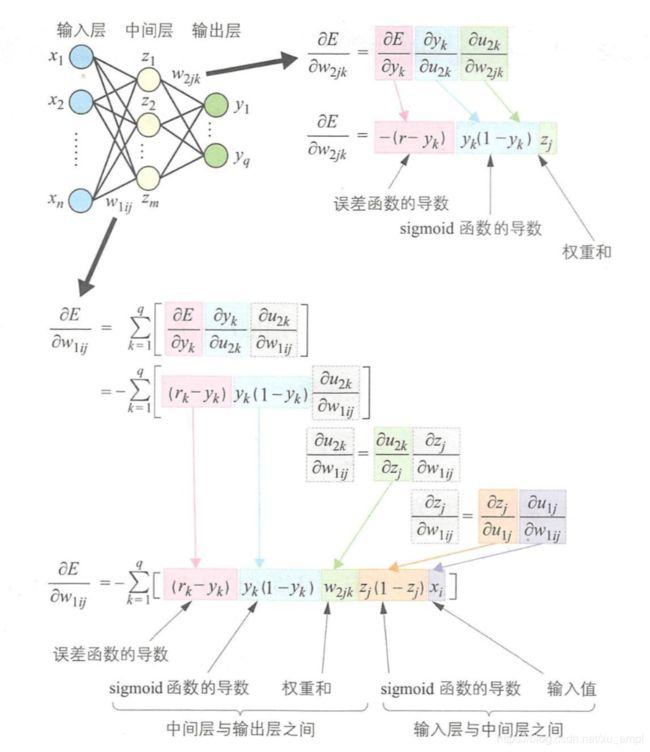
首先考虑输出层与中间层之间的连接权重 w 2 j k w_{2 j k} w2jk的调整。对连接权重 w 2 j k w_{2 j k} w2jk求导,得到下式: ∂ E ∂ w 2 j k = ∂ E ∂ y k ∂ y k ∂ u 2 k ∂ u 2 k ∂ w 2 j k ( 28 ) \frac{\partial E}{\partial w_{2 j k}}=\frac{\partial E}{\partial y_{k}} \frac{\partial y_{k}}{\partial u_{2 k}} \frac{\partial u_{2 k}}{\partial w_{2 j k}} \qquad(28) ∂w2jk∂E=∂yk∂E∂u2k∂yk∂w2jk∂u2k(28)在公式 ( 28 ) (28) (28)中,经过误差函数 E E E对输出 y k y_k yk求导,输出 y k y_k yk对激活值 u 2 k u_{2 k} u2k求导,激活值 u 2 k u_{2 k} u2k对连接权重 w 2 j k w_{2 j k} w2jk求导后,可得下式: ∂ E ∂ w 2 j k = − ( r k − y k ) y k ( 1 − y k ) z j ( 29 ) \frac{\partial E}{\partial w_{2 j k}}=-\left(r_{k}-y_{k}\right) y_{k}\left(1-y_{k}\right) z_{j} \qquad(29) ∂w2jk∂E=−(rk−yk)yk(1−yk)zj(29)所以,即使输出层有多个单元,对每个输出单元分别求导后,也能得到和公式 ( 16 ) (16) (16)相同的结果。下对输入层与中间层之间的连接权重 w 1 i j w_{1 i j} w1ij求导 ∂ E ∂ w 1 i j = ∑ k = 1 q [ ∂ E ∂ y k ∂ y k ∂ u 2 k ∂ y 2 k ∂ w 1 i j ] ( 30 ) \frac{\partial E}{\partial w_{1 i j}}=\sum_{k=1}^{q}\left[\frac{\partial E}{\partial y_{k}} \frac{\partial y_{k}}{\partial u_{2 k}} \frac{\partial y_{2 k}}{\partial w_{1 i j}}\right]\qquad(30) ∂w1ij∂E=k=1∑q[∂yk∂E∂u2k∂yk∂w1ij∂y2k](30)中间层的单元 j j j和输出层的所有单元相连,如公式 ( 30 ) (30) (30)所示,误差函数 E E E对连接权重 w 1 i j w_{1 i j} w1ij求导,就是对所有输出单元的导数进行加权求和,实际使用的是所有输出单元连接权重的总和。把误差函数和 sigmoid \text{sigmoid} sigmoid函数的导数代入到公式 ( 30 (30 (30中,得到下式 ∂ E ∂ w 1 i j = − ∑ k = 1 q [ ( r k − y k ) y k ( 1 − y k ) ∂ u 2 k ∂ w 1 i j ] ( 31 ) \frac{\partial E}{\partial w_{1 i j}}=-\sum_{k=1}^{q}\left[\left(r_{k}-y_{k}\right) y_{k}\left(1-y_{k}\right) \frac{\partial u_{2 k}}{\partial w_{1 i j}}\right] \qquad(31) ∂w1ij∂E=−k=1∑q[(rk−yk)yk(1−yk)∂w1ij∂u2k](31)由于连接权重 w 1 i j w_{1 i j} w1ij只对中间层 z j z_j zj的状态产生影响,公式 ( 31 ) (31) (31)中剩余部分求导后如下所示: ∂ u 2 k ∂ w 1 i j = ∂ u 2 k ∂ z j ∂ z j ∂ w 1 i j ( 32 ) \frac{\partial u_{2 k}}{\partial w_{1 i j}}=\frac{\partial u_{2 k}}{\partial z_{j}} \frac{\partial z_{j}}{\partial w_{1 i j}} \qquad(32) ∂w1ij∂u2k=∂zj∂u2k∂w1ij∂zj(32) ∂ z j ∂ w 1 j = ∂ z j ∂ u 1 j ∂ u 1 j ∂ w 1 j = z j ( 1 − z j ) x i ( 33 ) \frac{\partial z_{j}}{\partial w_{1 j}}=\frac{\partial z_{j}}{\partial u_{1 j}} \frac{\partial u_{1 j}}{\partial w_{1 j}}=z_{j}\left(1-z_{j}\right) x_{i} \qquad(33) ∂w1j∂zj=∂u1j∂zj∂w1j∂u1j=zj(1−zj)xi(33)激活值 u 2 k u_{2 k} u2k对 z j z_j zj求导得到连接权重 w 2 j k w_{2 j k} w2jk,结合公式 ( 33 ) (33) (33),就可以求得输入层与中间层之间的连接权重 w 1 i j w_{1 i j} w1ij的调整值,如公式 ( 34 ) (34) (34)所示: Δ w 1 i j = η ∑ k = 1 q [ ( r k − y k ) y k ( 1 − y k ) w 2 j k ] z j ( 1 − z j ) x i ( 34 ) \Delta w_{1 i j}=\eta \sum_{k=1}^{q}\left[\left(r_{k}-y_{k}\right) y_{k}\left(1-y_{k}\right) w_{2 j k}\right] z_{j}\left(1-z_{j}\right) x_{i} \qquad(34) Δw1ij=ηk=1∑q[(rk−yk)yk(1−yk)w2jk]zj(1−zj)xi(34)上述步骤汇总的结果如下图所示:
《图解深度学习》 山下隆义著 张弥译